535 lines
28 KiB
Markdown
535 lines
28 KiB
Markdown
# JoyRL论文阅读《Prioritized Experience Replay》 + Python代码
|
||
作者:Tom Schaul, John Quan, Ioannis Antonoglou and David Silver
|
||
|
||
实验室:Google DeepMind
|
||
|
||
邮箱:{schaul,johnquan,ioannisa,davidsilver}@google.com
|
||
|
||
论文地址:[https://arxiv.org/abs/1511.05952](https://arxiv.org/abs/1511.05952) Published as a conference paper at ICLR 2016
|
||
|
||
- **<u>*标题有问题*</u>**
|
||
|
||
|
||
## 一、提出背景
|
||
**深度强化学习算法**,结合了深度学习强大的环境感知能力和强化学习的决策能力,近年来被广泛应用于游戏、无人自主导航、多智能体协作以及推荐系统等各类人工智能新兴领域。强化学习作为机器学习的一个重要分支,其本质是智能体以“**试错**”的方式在与环境中学习策略,与常见的监督学习和非监督学习不同,强化学习强调智能体与环境之间的交互,在交互过程中通过不断学习来改变策略得到最大回报,以得到最优策略。
|
||
|
||
强化学习由于其算法特性,并没有现成的数据集,而仅靠单步获得的数据对未知的复杂环境信息进行感知决策并不高效可靠。DQN算法结合神经网络的同时,结合了**经验回放机制**,针对Q-learning的局限性,打消了采样数据相关性,使得数据分布变得更稳定。
|
||
|
||
但随着DQN算法的应用,研究人员发现,基于经验回放机制的DQN算法,仅采用**均匀采样**和**批次更新**,导致部分数量少但价值高的经验没有被高效的利用。针对上述情况,Deep Mind团队提出了**Prioritized Experience Replay(优先经验回放)机制**,本文将对该论文展开详细介绍。
|
||
|
||
## 二、摘要和结论
|
||
### 1 摘要
|
||
经验重放(Experience replay)使在线强化学习(Online reinforcement learning)智能体可以记住和重用过去的经验。先前的经验重放是从存储器中统一采样,只是以与最初经验的相同频率进行重采样,而不管其重要性如何。该论文开发了一个优先考虑经验的框架,以便更频繁地重播重要的数据,从而更有效地学习。文章中将优先经验回放机制与DQN网络结合,在49场比赛中有41场具有统一重播的DQN表现优于DQN。
|
||
|
||
### 2 结论
|
||
文章为经验回放机制及其几个变体,设计了可以扩展到大型重放内存的实现,发现优先级重放可以将学习速度提高2倍,并在Atari Baseline上带来了最新的性能。
|
||
|
||
## 三、基本理论
|
||
### 1 经验回放(Experience Replay):
|
||
- 创建一个经验池(Experience Replay Buffer),每一次Agent选择一个动作与环境交互就会储存一组数据$e_t = (s_t, a_t, r_t, s_{t+1})$到经验池中。
|
||
|
||
- 维护这个经验池(队列),当储存的数据组数到达一定的阈值,数据到就会从队列中被提取出来。
|
||
|
||
- 采用均匀采样的方式进行数据提取。
|
||
|
||
上述方法解决了经验数据的相关性(Correlated data)和非平稳分布(Non-stationary distribution)问题。它的做法是从以往的状态转移(经验)中**均匀采样**进行训练。优点是数据利用率高,一个样本被多次使用,且连续样本的相关性会使参数更新的方差(Variance)比较大,以此减少这种相关性。
|
||
|
||
然而,采用均匀采样方式存在的问题,作者举了例子如图所示: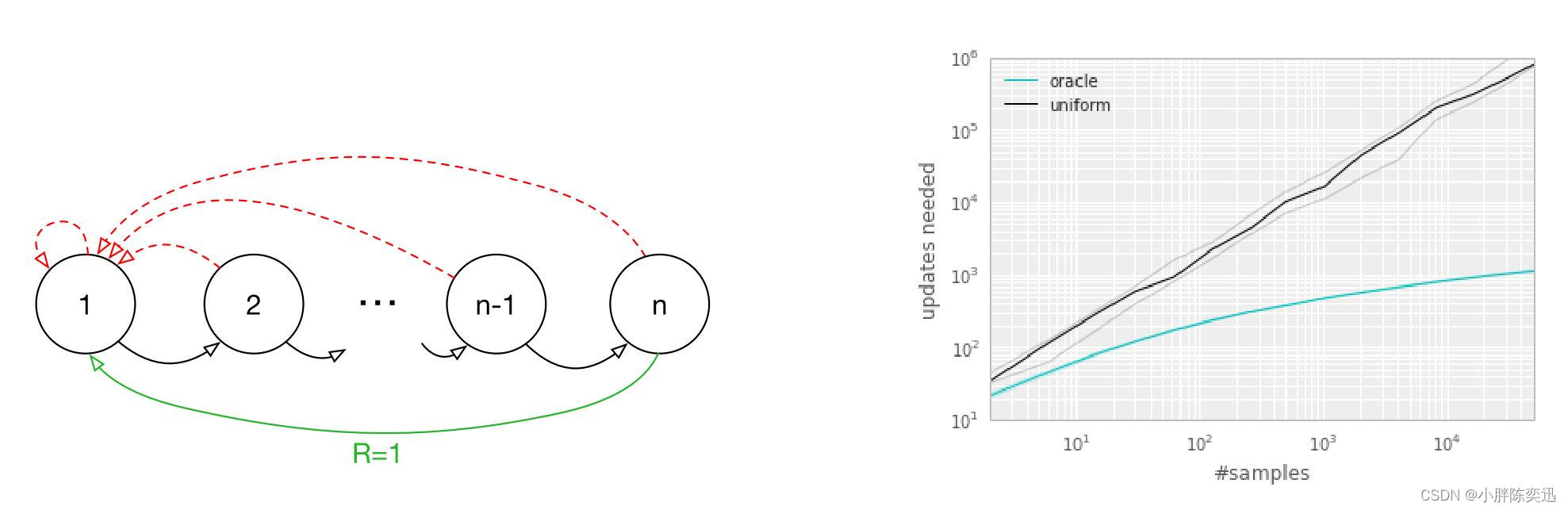
|
||
左图表示一个(稀疏奖励)环境有初始状态为1,有n个状态,两个可选动作,仅当选择绿色线条动作的时候可以得到 reward=1 的奖励;右图为实验结果,黑色曲线代表均匀采样的结果,蓝色曲线为研究人员提出的一个名为“oracle”的最优次序,即每次采样的transition均采用“最好”的结果,实验结果可看出每次采用最优次序的方法在稀疏奖励(Reward sparse)环境能够明显优于均匀采样。
|
||
|
||
那么如何在实际应用当中找到这个“最优”次序,即如何在采样前提前设计好一个次序,使得每次采样的数据都尽可能让agent高效学习呢?
|
||
### 2 优先经验回放(Prioritized Experience Replay,PER)
|
||
针对经验回放机制存在的问题,DeepMind团队提出了两方面的思考:要存储哪些经验(**which experiences to store**),以及要重放哪些经验(**which experiences to replay,and how to do so**)。论文中仅针对后者,即怎么样选取要采样的数据以及实验的方法做了详尽的说明和研究。
|
||
|
||
PER机制将TD-error(时序误差)作为衡量标准评估被采样数据的优先级。TD-error指在时序差分中**当前Q值**和它**目标Q值**的差值,误差越大即表示该数据对网络参数的更新越有帮助。贪婪(选取最大值)的采样TD-error大的数据训练,理论上会加速收敛,但随之而来也会面临以下问题:
|
||
|
||
- TD-error可看做对参数更新的信息增益,信息增益较大仅表示对于当前的价值网络参数而言增益较大,但却不能代表对于后续的价值网络没有较大的增益。若只贪婪的考虑信息增益来采样,当前TD-error较小的数据优先级会越来越低,后面会越来越难采样到该组数据。
|
||
|
||
- 贪婪的选择使得神经网络总是更新某一部分样本,即“经验的一个子集”,很可能导致陷入局部最优,亦或是过估计的发生。
|
||
|
||
针对上述PER存在的问题,作者在文中提出了一种随机抽样的方法,该方法介于纯贪婪和均匀随机之间,确保transition基于优先级的被采样概率是单调的,同时即使对于最低优先级的transition也保证非零的概率,随机抽样的方法将在***<u>1.3展开</u>***介绍。
|
||
|
||
## 四、相关改进工作
|
||
### 1 随机优先级(Stochastic Prioritization)
|
||
论文将采样transition $i$的概率定义为:
|
||
$$P(i)=\frac{p_i^\alpha}{\sum_k p_k^\alpha}$$
|
||
其中$p_i>0$表示transition $i$的优先级。指数$α$表示决定使用多少优先级,可看做一个trade-off因子,用来权衡uniform和greedy的程度,当$α=0$时表示均匀采样,$α=1$是表示贪婪(选取最大值)采样。
|
||
|
||
在DQN中:$\delta=y -Q(s, a)$, $\delta$表示TD-error,即每一步当前Q值与目标值$y$之间的差值,在更新过程中也是为了让$\delta^2$的期望尽可能的小。
|
||
|
||
文中将随机优先经验回放划分为以下两个类型:
|
||
|
||
a)直接的,基于比例的:**Proportional Prioritization**
|
||
|
||
b)间接的,基于排名的:**Rank-based Prioritization**
|
||
|
||
- **a)Proportional Prioritization**中,根据 $|\delta|$决定采样概率:
|
||
|
||
$$p_i=\left|\delta_i\right|+\epsilon$$
|
||
其中 $\delta$表示TD-eroor,$\epsilon$是一个大于0的常数,为了保证无论TD-error取值如何,采样概率$p_i$仍大于0,即仍有概率会被采样到。
|
||
- **b)Rank-based Prioritization**中,根据 $|\delta|$ 的 **排名(Rank)** 来决定采样概率:
|
||
|
||
$$p_i=\frac{1}{\operatorname{rank}(i)}$$
|
||
|
||
作者在文中对两种方法进行了比较:
|
||
|
||
**a)从理论层次分析:**
|
||
**proportional prioritization**优势在于可以直接获得 $|\delta|$ 的信息,也就是它的信息增益多一些;而**rank-based prioritization**则没有 $|\delta|$ 的信息,但其对异常点不敏感,因为异常点的TD-error过大或过小对rank值没有太大影响,也正因为此,**rank-based prioritization**具有更好的鲁棒性。
|
||
|
||
**b)从实验层次分析:**
|
||
结果如下图所示,可以看出这两种方法的表现大致相同。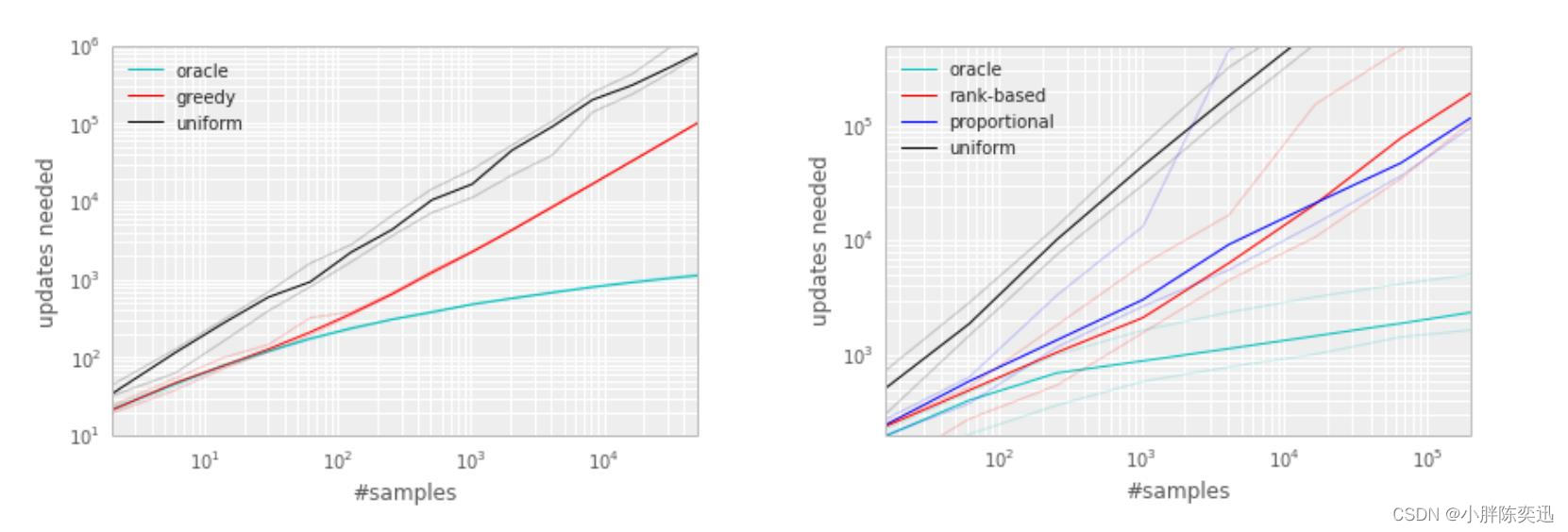
|
||
### 2 SumTree
|
||
Proportional Prioritization的实现较为复杂,可借助SumTree数据结构完成。SumTree是一种树形结构,每片树叶存储每个样本的优先级P,每个树枝节点只有两个分叉,节点的值是两个分叉的和,所以SumTree的顶端就是所有p的和。结构如下图([引自jaromiru.com](https://jaromiru.com/2016/11/07/lets-make-a-dqn-double-learning-and-prioritized-experience-replay/))所示, 顶层的节点是全部p的和。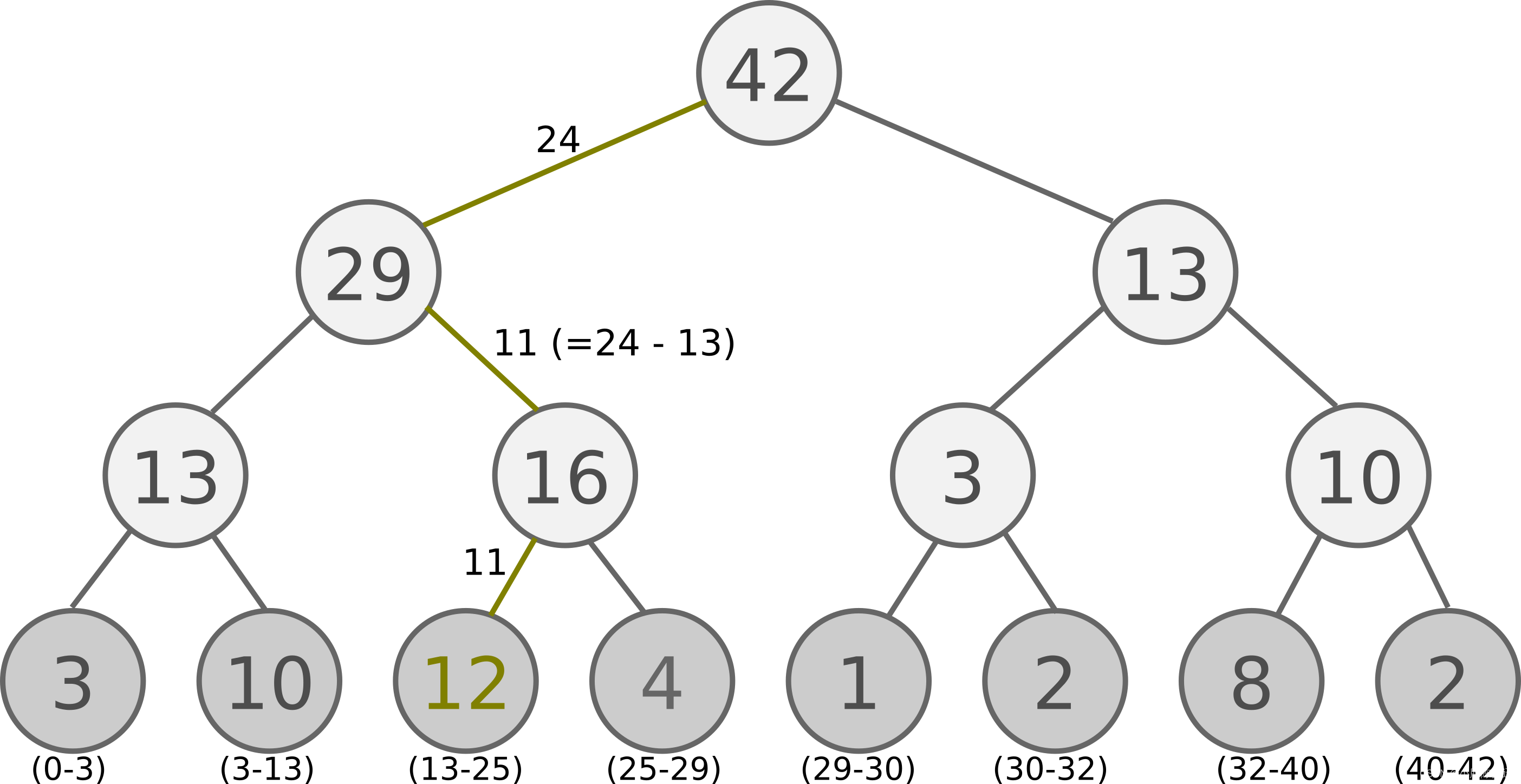
|
||
抽样时, 我们会将 p 的总和除以 batch size, 分成 batch size 多个区间,即$n={ sum(p) }/{batchsize}$.。如果将所有节点的优先级加起来是42, 我们如果抽6个样本, 这时的区间拥有的 priority 可能是这样:[0-7], [7-14], [14-21], [21-28], [28-35], [35-42]
|
||
|
||
然后在每个区间里随机选取一个数. 比如在第区间 [21-28] 里选到了24, 就按照这个 24 从最顶上的42开始向下搜索. 首先看到最顶上 42 下面有两个 child nodes, 拿着手中的24对比左边的 child 29, 如果左边的 child 比自己手中的值大, 那我们就走左边这条路, 接着再对比 29 下面的左边那个点 13, 这时, 手中的 24 比 13 大, 那我们就走右边的路, 并且将手中的值根据 13 修改一下, 变成 24-13 = 11. 接着拿着 11 和 13 左下角的 12 比, 结果 12 比 11 大, 那我们就选 12 当做这次选到的 priority, 并且也选择 12 对应的数据。
|
||
|
||
以上面的树结构为例,根节点是42,如果要采样一个样本,我们可以在[0,42]之间做均匀采样,采样到哪个区间,就是哪个样本。比如我们采样到了26, 在(25-29)这个区间,那么就是第四个叶子节点被采样到。而注意到第三个叶子节点优先级最高,是12,它的区间13-25也是最长的,所以它会比其他节点更容易被采样到。
|
||
|
||
如果要采样两个样本,我们可以在[0,21],[21,42]两个区间做均匀采样,方法和上面采样一个样本类似。
|
||
### 3 消除偏差(Annealing the Bias)
|
||
使用优先经验回放还存在一个问题是改变了状态的分布,DQN中引入经验池是为了解决数据相关性,使数据(尽量)独立同分布。但是使用优先经验回放又改变了状态的分布,这样势必会引入偏差bias,对此,文中使用重要性采样结合退火因子来消除引入的偏差。
|
||
|
||
在DQN中,梯度的计算如下所示:
|
||
$$
|
||
\nabla_{\theta_i} L\left(\theta_i\right)=\mathbb{E}_{s, a, r, s^{\prime}}\left[\left(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_i\right)-Q\left(s, a ; \theta_i\right)\right) \nabla_{\theta_i} Q\left(s, a ; \theta_i\right)\right](1)
|
||
$$
|
||
在随机梯度下降(SGD)中可表示为:
|
||
$$
|
||
\nabla_\theta L(\theta)=\delta \nabla_\theta Q(s, a)
|
||
$$
|
||
而重要性采样,就是给这个梯度加上一个权重$w$
|
||
$$
|
||
\nabla_\theta L(\theta)=w \delta \nabla_\theta Q(s, a)
|
||
$$
|
||
重要性采样权重$w_i$在文中定义为:
|
||
$$
|
||
w_i=\left(\frac{1}{N} \cdot \frac{1}{P(i)}\right)^\beta
|
||
$$
|
||
$N$ 表示Buffer里的样本数,而 $\beta$ 是一个超参数,用来决定多大程度想抵消 Prioritized Experience Replay对收敛结果的影响。如果 $\beta=0$,表示完全不使用重要性采样 ;$\beta=1$时表示完全抵消掉影响,由于 $(s, a)$ 不再是均匀分布随机选出来的了,而是以 $P(i)$ 的概率选出来,因此,如果 $\beta=1$ , 那么 $w$ 和 $P(i)$ 就正好抵消了,于是Prioritized Experience Replay的作用也就被抵消了,即$\beta=1$等同于DQN中的 Experience Replay。
|
||
|
||
为了稳定性,我们需要对权重 $w$ 归一化,但是不用真正意义上的归一化,只要除上 $\max _i w_i$ 即可,即:
|
||
|
||
$$
|
||
w_j=(N * P(j))^{-\beta} / \max _i\left(w_i\right)
|
||
$$
|
||
|
||
归一化后的 $w_i$ 在编写代码时可推导转化为:
|
||
|
||
$$
|
||
w_j=\frac{(N * P(j))^{-\beta}}{\max _i\left(w_i\right)}=\frac{(N * P(j))^{-\beta}}{\max _i\left((N * P(i))^{-\beta}\right)}=\frac{(P(j))^{-\beta}}{\max _i\left((P(i))^{-\beta}\right)}=\left(\frac{P_j}{\min _i P(i)}\right)^{-\beta}
|
||
$$
|
||
|
||
## 五、PER代码
|
||
### 1 Prioritized Replay DQN 算法流程
|
||
**算法输入**:迭代轮数 $T$ ,状态特征维度 $n$ ,动作集 $A$ ,步长 $\alpha$ ,采样权重系数 $\beta$ ,衰减因子 $\gamma$ ,探索率 $\epsilon$ ,当前 $Q$ 网络 $Q$ ,目标 $\mathrm{Q}$ 网络 $Q^{\prime}$ ,批量梯度下降的样本数 $m$ ,目标 $\mathrm{Q}$ 网络参数更新频率 $C$ ,SumTree的叶子节点数 $S$ 。
|
||
|
||
**输出**: Q网络参数。
|
||
|
||
1. 随机初始化所有的状态和动作对应的价值 $Q$. 随机初始化当前 $\mathrm{Q}$ 网络的所有参数 $w$, 初始化目标Q网络 $Q^{\prime}$ 的参数 $w^{\prime}=w$ 。初始化经验回放SumTree 的默认数据结构,所有SumTree的 $S$ 个叶子节点的优先级 $p_j$ 为 1 。
|
||
|
||
2. for i from 1 to $T$ ,进行迭代。
|
||
|
||
a) 初始化S为当前状态序列的第一个状态,得到其特征向量 $\phi(S)$
|
||
|
||
b) 在 $\mathrm{Q}$ 网络中使用 $\phi(S)$ 作为输入,得到 $\mathrm{Q}$ 网络的所有动作对应的 $\mathrm{Q}$ 值输出。用 $\epsilon$ 一贪婪法在当前 $\mathrm{Q}$ 值输出中选择对应的动作 $A$
|
||
|
||
c) 在状态 $S$ 执行当前动作 $A$, 得到新状态 $S^{\prime}$ 对应的特征向量 $\phi\left(S^{\prime}\right)$ 和奖励 $R$, 是否终止状态is_end
|
||
|
||
d) 将 $\left\{\phi(S), A, R, \phi\left(S^{\prime}\right), i s_{-} e n d\right\}$ 这个五元组存入SumTree
|
||
|
||
e) $S=S^{\prime}$
|
||
|
||
f) 从SumTree中采样 $m$ 个样本 $\left\{\phi\left(S_j\right), A_j, R_j, \phi\left(S_j^{\prime}\right), i s_{-} e n d_j\right\}, j=1,2 .,,, m$,每个样本被采样的概率基于 $P(j)=\frac{p_j}{\sum_i\left(p_i\right)}$ ,损失函数权重 $w_j=(N * P(j))^{-\beta} / \max _i\left(w_i\right)$ ,计算当前目标Q值 $y_j$ :
|
||
|
||
$$
|
||
y_j= \begin{cases}R_j & \text { is end }_j \text { is true } \\ R_j+\gamma Q^{\prime}\left(\phi\left(S_j^{\prime}\right), \arg \max _{a^{\prime}} Q\left(\phi\left(S_j^{\prime}\right), a, w\right), w^{\prime}\right) & \text { is end }_j \text { is false }\end{cases}
|
||
$$
|
||
|
||
g)使用均方差损失函数 $\frac{1}{m} \sum_{j=1}^m w_j\left(y_j-Q\left(\phi\left(S_j\right), A_j, w\right)\right)^2$ ,通过神经网络的梯度反向传播来更新Q网络的所有参数 $w$
|
||
|
||
h) 重新计算所有样本的TD误差 $\delta_j=y_j-Q\left(\phi\left(S_j\right), A_j, w\right)$,更新SumTree中所有节点的优先级 $p_j=\left|\delta_j\right|$
|
||
|
||
i) 如果 $\mathrm{i} \% \mathrm{C}=1$, 则更新目标 $\mathrm{Q}$ 网络参数 $w^{\prime}=w$
|
||
|
||
j) 如果 $S^{\prime}$ 是终止状态,当前轮迭代完毕,否则转到步骤b)
|
||
|
||
|
||
### 2 相关代码
|
||
该部分代码可直接在程序里调用,其中ReplayBuffer()这个类是传统的的经验回放;PrioritizedReplayBuffer(ReplayBuffer)这个类是优先经验回放。
|
||
|
||
```python
|
||
import numpy as np
|
||
import random
|
||
|
||
from segment_tree import SumSegmentTree, MinSegmentTree
|
||
|
||
|
||
class ReplayBuffer(object):
|
||
def __init__(self, size):
|
||
"""Create Replay buffer.
|
||
|
||
Parameters
|
||
----------
|
||
size: int
|
||
Max number of transitions to store in the buffer. When the buffer
|
||
overflows the old memories are dropped.
|
||
"""
|
||
self._storage = []
|
||
self._maxsize = size
|
||
self._next_idx = 0
|
||
|
||
def __len__(self):
|
||
return len(self._storage)
|
||
|
||
def add(self, obs_t, action, reward, obs_tp1, done):
|
||
data = (obs_t, action, reward, obs_tp1, done)
|
||
|
||
if self._next_idx >= len(self._storage):
|
||
self._storage.append(data)
|
||
else:
|
||
self._storage[self._next_idx] = data
|
||
self._next_idx = (self._next_idx + 1) % self._maxsize
|
||
|
||
def _encode_sample(self, idxes):
|
||
obses_t, actions, rewards, obses_tp1, dones = [], [], [], [], []
|
||
for i in idxes:
|
||
data = self._storage[i]
|
||
obs_t, action, reward, obs_tp1, done = data
|
||
obses_t.append(np.array(obs_t, copy=False))
|
||
actions.append(np.array(action, copy=False))
|
||
rewards.append(reward)
|
||
obses_tp1.append(np.array(obs_tp1, copy=False))
|
||
dones.append(done)
|
||
return np.array(obses_t), np.array(actions), np.array(rewards), np.array(obses_tp1), np.array(dones)
|
||
|
||
def sample(self, batch_size):
|
||
"""Sample a batch of experiences.
|
||
|
||
Parameters
|
||
----------
|
||
batch_size: int
|
||
How many transitions to sample.
|
||
|
||
Returns
|
||
-------
|
||
obs_batch: np.array
|
||
batch of observations
|
||
act_batch: np.array
|
||
batch of actions executed given obs_batch
|
||
rew_batch: np.array
|
||
rewards received as results of executing act_batch
|
||
next_obs_batch: np.array
|
||
next set of observations seen after executing act_batch
|
||
done_mask: np.array
|
||
done_mask[i] = 1 if executing act_batch[i] resulted in
|
||
the end of an episode and 0 otherwise.
|
||
"""
|
||
idxes = [random.randint(0, len(self._storage) - 1) for _ in range(batch_size)]
|
||
return self._encode_sample(idxes)
|
||
|
||
|
||
class PrioritizedReplayBuffer(ReplayBuffer):
|
||
def __init__(self, size, alpha):
|
||
"""Create Prioritized Replay buffer.
|
||
|
||
Parameters
|
||
----------
|
||
size: int
|
||
Max number of transitions to store in the buffer. When the buffer
|
||
overflows the old memories are dropped.
|
||
alpha: float
|
||
how much prioritization is used
|
||
(0 - no prioritization, 1 - full prioritization)
|
||
|
||
See Also
|
||
--------
|
||
ReplayBuffer.__init__
|
||
"""
|
||
super(PrioritizedReplayBuffer, self).__init__(size)
|
||
assert alpha >= 0
|
||
self._alpha = alpha
|
||
|
||
it_capacity = 1
|
||
while it_capacity < size:
|
||
it_capacity *= 2
|
||
|
||
self._it_sum = SumSegmentTree(it_capacity)
|
||
self._it_min = MinSegmentTree(it_capacity)
|
||
self._max_priority = 1.0
|
||
|
||
def add(self, *args, **kwargs):
|
||
"""See ReplayBuffer.store_effect"""
|
||
idx = self._next_idx
|
||
super().add(*args, **kwargs)
|
||
self._it_sum[idx] = self._max_priority ** self._alpha
|
||
self._it_min[idx] = self._max_priority ** self._alpha
|
||
|
||
def _sample_proportional(self, batch_size):
|
||
res = []
|
||
p_total = self._it_sum.sum(0, len(self._storage) - 1)
|
||
every_range_len = p_total / batch_size
|
||
for i in range(batch_size):
|
||
mass = random.random() * every_range_len + i * every_range_len
|
||
idx = self._it_sum.find_prefixsum_idx(mass)
|
||
res.append(idx)
|
||
return res
|
||
|
||
def sample(self, batch_size, beta):
|
||
"""Sample a batch of experiences.
|
||
|
||
compared to ReplayBuffer.sample
|
||
it also returns importance weights and idxes
|
||
of sampled experiences.
|
||
|
||
|
||
Parameters
|
||
----------
|
||
batch_size: int
|
||
How many transitions to sample.
|
||
beta: float
|
||
To what degree to use importance weights
|
||
(0 - no corrections, 1 - full correction)
|
||
|
||
Returns
|
||
-------
|
||
obs_batch: np.array
|
||
batch of observations
|
||
act_batch: np.array
|
||
batch of actions executed given obs_batch
|
||
rew_batch: np.array
|
||
rewards received as results of executing act_batch
|
||
next_obs_batch: np.array
|
||
next set of observations seen after executing act_batch
|
||
done_mask: np.array
|
||
done_mask[i] = 1 if executing act_batch[i] resulted in
|
||
the end of an episode and 0 otherwise.
|
||
weights: np.array
|
||
Array of shape (batch_size,) and dtype np.float32
|
||
denoting importance weight of each sampled transition
|
||
idxes: np.array
|
||
Array of shape (batch_size,) and dtype np.int32
|
||
idexes in buffer of sampled experiences
|
||
"""
|
||
assert beta > 0
|
||
|
||
idxes = self._sample_proportional(batch_size)
|
||
|
||
weights = []
|
||
p_min = self._it_min.min() / self._it_sum.sum()
|
||
max_weight = (p_min * len(self._storage)) ** (-beta)
|
||
|
||
for idx in idxes:
|
||
p_sample = self._it_sum[idx] / self._it_sum.sum()
|
||
weight = (p_sample * len(self._storage)) ** (-beta)
|
||
weights.append(weight / max_weight)
|
||
weights = np.array(weights)
|
||
encoded_sample = self._encode_sample(idxes)
|
||
return tuple(list(encoded_sample) + [weights, idxes])
|
||
|
||
def update_priorities(self, idxes, priorities):
|
||
"""Update priorities of sampled transitions.
|
||
|
||
sets priority of transition at index idxes[i] in buffer
|
||
to priorities[i].
|
||
|
||
Parameters
|
||
----------
|
||
idxes: [int]
|
||
List of idxes of sampled transitions
|
||
priorities: [float]
|
||
List of updated priorities corresponding to
|
||
transitions at the sampled idxes denoted by
|
||
variable `idxes`.
|
||
"""
|
||
assert len(idxes) == len(priorities)
|
||
for idx, priority in zip(idxes, priorities):
|
||
assert priority > 0
|
||
assert 0 <= idx < len(self._storage)
|
||
self._it_sum[idx] = priority ** self._alpha
|
||
self._it_min[idx] = priority ** self._alpha
|
||
|
||
self._max_priority = max(self._max_priority, priority)
|
||
|
||
```
|
||
以上代码调用的数据结构SumTree,代码如下:
|
||
|
||
```python
|
||
import operator
|
||
|
||
|
||
class SegmentTree(object):
|
||
def __init__(self, capacity, operation, neutral_element):
|
||
"""Build a Segment Tree data structure.
|
||
|
||
https://en.wikipedia.org/wiki/Segment_tree
|
||
|
||
Can be used as regular array, but with two
|
||
important differences:
|
||
|
||
a) setting item's value is slightly slower.
|
||
It is O(lg capacity) instead of O(1).
|
||
b) user has access to an efficient ( O(log segment size) )
|
||
`reduce` operation which reduces `operation` over
|
||
a contiguous subsequence of items in the array.
|
||
|
||
Paramters
|
||
---------
|
||
capacity: int
|
||
Total size of the array - must be a power of two.
|
||
operation: lambda obj, obj -> obj
|
||
and operation for combining elements (eg. sum, max)
|
||
must form a mathematical group together with the set of
|
||
possible values for array elements (i.e. be associative)
|
||
neutral_element: obj
|
||
neutral element for the operation above. eg. float('-inf')
|
||
for max and 0 for sum.
|
||
"""
|
||
assert capacity > 0 and capacity & (capacity - 1) == 0, "capacity must be positive and a power of 2."
|
||
self._capacity = capacity
|
||
self._value = [neutral_element for _ in range(2 * capacity)]
|
||
self._operation = operation
|
||
|
||
def _reduce_helper(self, start, end, node, node_start, node_end):
|
||
if start == node_start and end == node_end:
|
||
return self._value[node]
|
||
mid = (node_start + node_end) // 2
|
||
if end <= mid:
|
||
return self._reduce_helper(start, end, 2 * node, node_start, mid)
|
||
else:
|
||
if mid + 1 <= start:
|
||
return self._reduce_helper(start, end, 2 * node + 1, mid + 1, node_end)
|
||
else:
|
||
return self._operation(
|
||
self._reduce_helper(start, mid, 2 * node, node_start, mid),
|
||
self._reduce_helper(mid + 1, end, 2 * node + 1, mid + 1, node_end)
|
||
)
|
||
|
||
def reduce(self, start=0, end=None):
|
||
"""Returns result of applying `self.operation`
|
||
to a contiguous subsequence of the array.
|
||
|
||
self.operation(arr[start], operation(arr[start+1], operation(... arr[end])))
|
||
|
||
Parameters
|
||
----------
|
||
start: int
|
||
beginning of the subsequence
|
||
end: int
|
||
end of the subsequences
|
||
|
||
Returns
|
||
-------
|
||
reduced: obj
|
||
result of reducing self.operation over the specified range of array elements.
|
||
"""
|
||
if end is None:
|
||
end = self._capacity
|
||
if end < 0:
|
||
end += self._capacity
|
||
end -= 1
|
||
return self._reduce_helper(start, end, 1, 0, self._capacity - 1)
|
||
|
||
def __setitem__(self, idx, val):
|
||
# index of the leaf
|
||
idx += self._capacity
|
||
self._value[idx] = val
|
||
idx //= 2
|
||
while idx >= 1:
|
||
self._value[idx] = self._operation(
|
||
self._value[2 * idx],
|
||
self._value[2 * idx + 1]
|
||
)
|
||
idx //= 2
|
||
|
||
def __getitem__(self, idx):
|
||
assert 0 <= idx < self._capacity
|
||
return self._value[self._capacity + idx]
|
||
|
||
|
||
class SumSegmentTree(SegmentTree):
|
||
def __init__(self, capacity):
|
||
super(SumSegmentTree, self).__init__(
|
||
capacity=capacity,
|
||
operation=operator.add,
|
||
neutral_element=0.0
|
||
)
|
||
|
||
def sum(self, start=0, end=None):
|
||
"""Returns arr[start] + ... + arr[end]"""
|
||
return super(SumSegmentTree, self).reduce(start, end)
|
||
|
||
def find_prefixsum_idx(self, prefixsum):
|
||
"""Find the highest index `i` in the array such that
|
||
sum(arr[0] + arr[1] + ... + arr[i - i]) <= prefixsum
|
||
|
||
if array values are probabilities, this function
|
||
allows to sample indexes according to the discrete
|
||
probability efficiently.
|
||
|
||
Parameters
|
||
----------
|
||
perfixsum: float
|
||
upperbound on the sum of array prefix
|
||
|
||
Returns
|
||
-------
|
||
idx: int
|
||
highest index satisfying the prefixsum constraint
|
||
"""
|
||
assert 0 <= prefixsum <= self.sum() + 1e-5
|
||
idx = 1
|
||
while idx < self._capacity: # while non-leaf
|
||
if self._value[2 * idx] > prefixsum:
|
||
idx = 2 * idx
|
||
else:
|
||
prefixsum -= self._value[2 * idx]
|
||
idx = 2 * idx + 1
|
||
return idx - self._capacity
|
||
|
||
|
||
class MinSegmentTree(SegmentTree):
|
||
def __init__(self, capacity):
|
||
super(MinSegmentTree, self).__init__(
|
||
capacity=capacity,
|
||
operation=min,
|
||
neutral_element=float('inf')
|
||
)
|
||
|
||
def min(self, start=0, end=None):
|
||
"""Returns min(arr[start], ..., arr[end])"""
|
||
|
||
return super(MinSegmentTree, self).reduce(start, end)
|
||
|
||
```
|
||
## 六、总结与展望
|
||
虽然PER在采用**相同的交互次数**时会获得更高的性能,更加适合**稀疏奖励**或者**高奖励难以获得**的复杂环境,但其花费同样的时间,性能不一定更高,即花的时间要多三四倍。(参考文献6)针对PER耗时问题提出自己的实验和结论,其将总采样消耗的时间划分为三个部分(**采样时间、PER更新时间、算法更新时间**)进行实验,发现添加了原始PER的网络耗时反而更高。
|
||
|
||
> The first one is the sample, which needs to search on the sum-tree. When the capacity of EM goes larger, the sampling time, whose time complexity is O(logN), becomes a bottleneck.
|
||
The second one is PER update, which is the same time complexity as sampling.
|
||
The last one is the DDQN or DDPG update, which is executed on GPU.
|
||
We measure the time cost to correct all priorities of EM(capacity is 106). All data must be predicted by DDQN on GPU, it needs 150+ s. We can see that the update cost is very high.
|
||
|
||
同时笔者本人及导师在实验时也发现了同样的问题,PER对于目前稀疏奖励环境,理论上应该是有成效,但由于现阶段大家为了更快探索,更快收敛,不仅在环境感知层面做了不少trick,奖励函数也设计得越来越丰富,PER耗时长的缺点被无限放大,故而大家在选择经验回放池的时候尽可能考虑自己的实际情况,不要拿着Rainbow算法就开始魔改,效果可能会适得其反。
|
||
## 参考文献
|
||
1.[https://arxiv.org/pdf/1511.05952.pdf](https://arxiv.org/pdf/1511.05952.pdf)
|
||
|
||
2.[https://zhuanlan.zhihu.com/p/310630316](https://zhuanlan.zhihu.com/p/310630316)
|
||
|
||
3.[https://zhuanlan.zhihu.com/p/160186240](https://zhuanlan.zhihu.com/p/160186240)
|
||
|
||
4.[https://zhuanlan.zhihu.com/p/137880325](https://zhuanlan.zhihu.com/p/137880325)
|
||
|
||
5.[https://jaromiru.com/2016/11/07/lets-make-a-dqn-double-learning-and-prioritized-experience-replay/](https://jaromiru.com/2016/11/07/lets-make-a-dqn-double-learning-and-prioritized-experience-replay/)
|
||
|
||
6.[https://www.mdpi.com/2076-3417/10/19/6925/pdf](https://www.mdpi.com/2076-3417/10/19/6925/pdf)
|
||
|
||
7.[蘑菇书EasyRL](https://gitcode.net/mirrors/datawhalechina/easy-rl?utm_source=csdn_github_accelerator)
|
||
|
||
## 个人简介
|
||
|
||
李成阳
|
||
|
||
|
||
|