7.9 KiB
针对连续动作的 DQN
方案 1 & 方案 2
跟基于策略梯度的方法比起来,DQN 是比较稳的。策略梯度是没有太多游戏是玩得起来的,策略梯度比较不稳,在没有 近端策略优化 之前,我们很难用策略梯度做什么事情。DQN 相对而言是比较稳的。最早 DeepMind 的论文拿深度强化学习来玩雅达利的游戏,用的就是 DQN。DQN 比较容易训练的一个理由是:在 DQN 里面,你只要能够估计出Q函数,就保证你一定可以找到一个比较好的策略。也就是你只要能够估计出Q函数,就保证你可以改进策略。而估计Q函数这件事情,是比较容易的,因为它就是一个回归问题。在回归问题里面, 你可以轻易地知道模型学习得是不是越来越好,只要看那个回归的损失有没有下降,你就知道说模型学习得好不好,所以估计Q函数相较于学习一个策略是比较容易的。你只要估计Q函数,就可以保证说现在一定会得到比较好的策略。所以一般而言 DQN 比较容易操作。
DQN 其实存在一些问题,最大的问题是它不太容易处理连续动作。很多时候动作是连续的,比如我们玩雅达利的游戏,智能体只需要决定比如说上下左右,这种动作是离散的。那很多时候动作是连续的。举例来说假设智能体要做的事情是开自驾车,它要决定说它方向盘要左转几度, 右转几度,这是连续的。假设智能体是一个机器人,它身上有 50 个 关节,它的每一个动作就对应到它身上的这 50 个关节的角度。而那些角度也是连续的。所以很多时候动作并不是一个离散的东西,它是一个向量。在这个向量里面,它的每一个维度都有一个对应的值,都是实数,它是连续的。假设动作是连续的,做 DQN 就会有困难。因为在做 DQN 里面一个很重要的一步是你要能够解这个优化问题。估计出 Q函数Q(s,a) 以后,必须要找到一个 $a$,它可以让 Q(s,a) 最大,如下式所示。
a=\arg \max _{a} Q(s, a)
假设$a$是离散的,即$a$的可能性都是有限的。举例来说,雅达利的小游戏里面,a 就是上下左右跟开火,它是有限的,我们可以把每一个可能的动作都带到 Q 里面算它的 Q 值。但假如$a$是连续的,你无法穷举所有可能的连续动作,试试看哪一个连续动作可以让 Q 的值最大。
怎么解这个问题呢?就有各种不同的方案。
第一个方案是假设你不知道怎么解这个问题,因为$a$是没有办法穷举的,怎么办?我们可以采样出 N 个可能的 $a$:\left\{a_{1}, a_{2}, \cdots, a_{N}\right\} ,一个一个带到 Q函数里面,看谁最大。这个方法其实也不会太不高效, 因为你在运算的时候会使用 GPU,一次会把 N 个连续动作都丢到 Q函数里面,一次得到 N 个 Q 值,然后看谁最大。当然这不是一个非常精确的做法,因为你没有办法做太多的采样, 所以你估计出来的 Q 值,最后决定的动作可能不是非常的精确,这是第一个方案。
第二个方案是什么呢?既然要解的是一个优化问题(optimization problem),其实是要最大化目标函数(objective function),要最大化一个东西, 就可以用梯度上升。我们就把$a$当作是参数,然后要找一组$a$去最大化Q函数,就用梯度上升去更新 a 的值,最后看看能不能找到一个$a$去最大化Q函数,也就是目标函数。当然这样子你会遇到全局最大值(global maximum)的问题, 就不见得能够真的找到最优的结果,而且这个运算量显然很大, 因为你要迭代地更新 $a$。我们训练一个网络就很花时间了。如果你用梯度上升的方法来处理连续的问题, 等于是你每次要决定采取哪一个动作的时候,都还要做一次训练网络的过程,显然运算量是很大的。这是第二个方案。
方案 3:设计网络
第三个方案是特别设计一个网络的架构,特别设计Q函数,使得解 arg max 的问题变得非常容易。也就是这边的Q函数不是一个一般的Q函数,特别设计一下它的样子,让你要找让这个Q函数最大的 a 的时候非常容易。
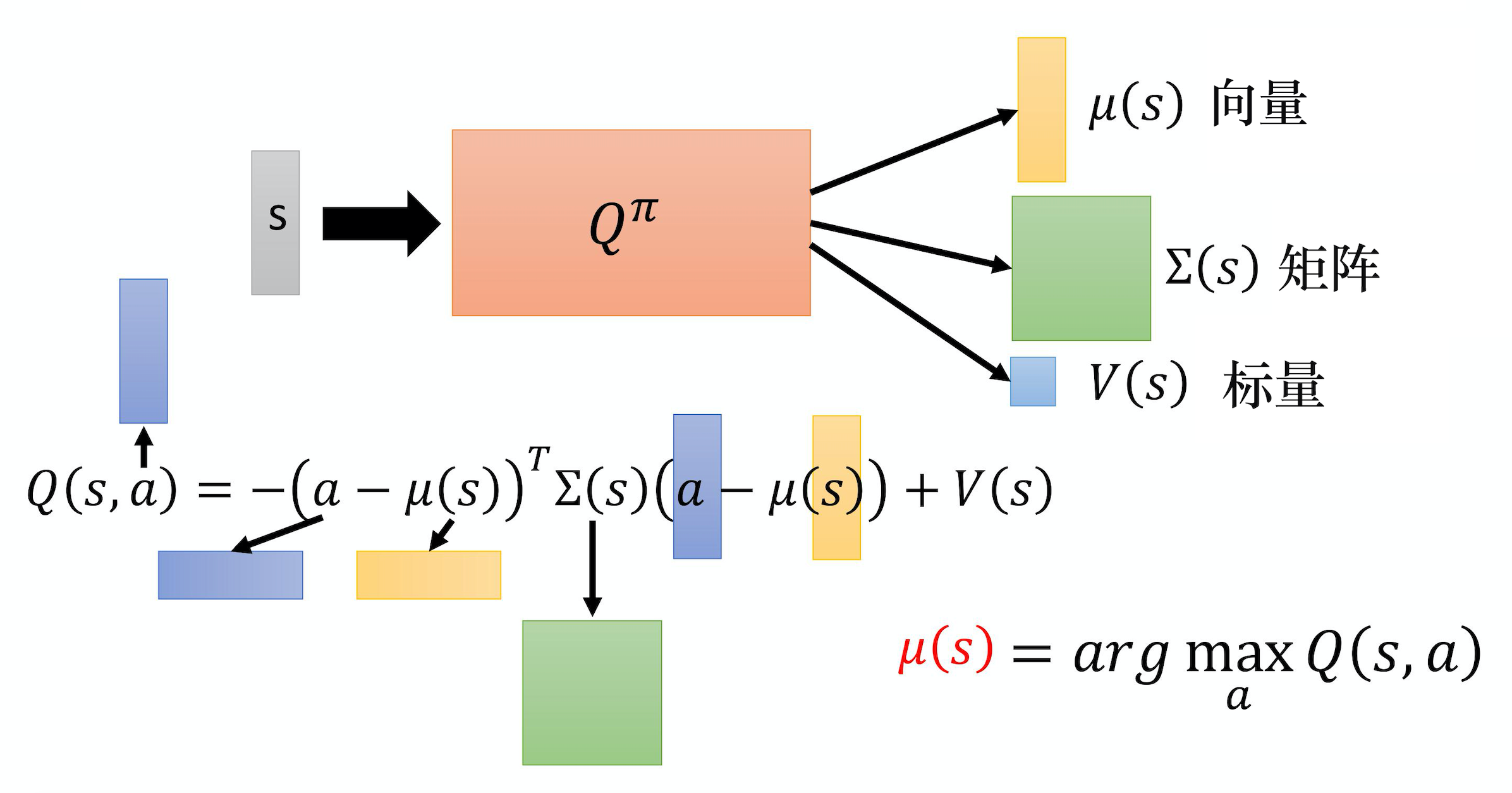
下图是一个例子,这边有Q函数,这个Q函数的做法是这样。
通常输入状态 s 就是一个图像,可以用一个向量或一个矩阵来表示。
输入 $s$,Q函数会输出 3 个东西。它会输出 $\mu(s)$,这是一个向量。它会输出 \Sigma(s) ,这是一个矩阵。它会输出 $V(s)$,这是一个标量。
输出这 3 个东西以后,我们知道Q函数其实是吃一个$s$跟 $a$,然后决定一个值。Q函数意思是说在某一个状态,采取某一个动作的时候,你期望的奖励有多大。到目前为止这个Q函数只吃 $s$,它还没有吃$a$进来,a 在哪里呢?当这个Q函数吐出 $\mu$、 \Sigma 跟 V 的时候,我们才把$a$引入,用$a$跟 \mu(s)、\Sigma(s)、V 互相作用一下,你才算出最终的 Q 值。
$a$怎么和这 3 个东西互相作用呢?实际上 $Q(s,a)$,Q函数的运作方式是先输入 $s$,让你得到 \mu,\Sigma 跟 $V$。然后再输入 $a$,然后接下来把$a$跟 \mu 相减。注意一下$a$现在是连续的动作,所以它也是一个向量。假设你现在是要操作机器人的话,这个向量的每一个维度,可能就对应到机器人的某一个关节,它的数值就是关节的角度,所以$a$是一个向量。把向量 a 减掉向量 $\mu$,取转置,所以它是一个横的向量。\Sigma 是一个矩阵。然后$a$减掉 \mu(s) ,a 和 \mu(s) 都是向量,减掉以后还是一个竖的向量。所以 -(a-\mu(s))^{T} \Sigma(s)(a-\mu(s))+V(s) 是一个标量,这个数值就是 Q 值 $Q(s,a)$。
假设 Q(s,a) 定义成这个样子,我们要怎么找到一个$a$去最大化这个 Q 值呢?这个方案非常简单。因为 (a-\mu(s))^{T} \Sigma(s)(a-\mu(s)) 一定是正的,它前面乘上一个负号,所以第一项就假设我们不看这个负号的话,第一项的值越小,最终的 Q 值就越大。因为我们是把 V(s) 减掉第一项,所以第一项的值越小,最后的 Q 值就越大。怎么让第一项的值最小呢?你直接把$a$代入 \mu 的值,让它变成 0,就会让第一项的值最小。
\Sigma 一定是正定的。因为这个东西就像是高斯分布(Gaussian distribution),所以 \mu 就是高斯分布的均值,\Sigma 就是高斯分布的方差。但方差是一个正定(positive definite)的矩阵,怎么样让这个 \Sigma 一定是正定的矩阵呢?其实在 Q^{\pi} 里面,它不是直接输出 $\Sigma$,如果直接输出 一个 $\Sigma$, 它不一定是正定的矩阵。它其实是输出 一个矩阵,然后再把那个矩阵跟另外一个矩阵做转置相乘, 然后可以确保 \Sigma 是正定的。这边要强调的点就是说,实际上它不是直接输出一个矩阵。你再去那个论文里面查看一下它的技巧,它可以保证说 \Sigma 是正定的。
你把$a$代入 \mu(s) 以后,你可以让 Q 的值最大。所以假设要你 arg max Q 函数,如下式所示。
\mu(s)=\arg \max _{a} Q(s, a)
虽然一般而言,若 Q 是一个一般的函数, 你很难算,但是我们这边设计了 Q 这个函数,a 只要设 $\mu(s)$,我们就得到最大值。你在解这个 arg max 的问题的时候就变得非常容易。所以 DQN 也可以用在连续的情况,只是有一些局限,就是函数不能够随便乱设,它必须有一些限制。
方案 4:不使用DQN
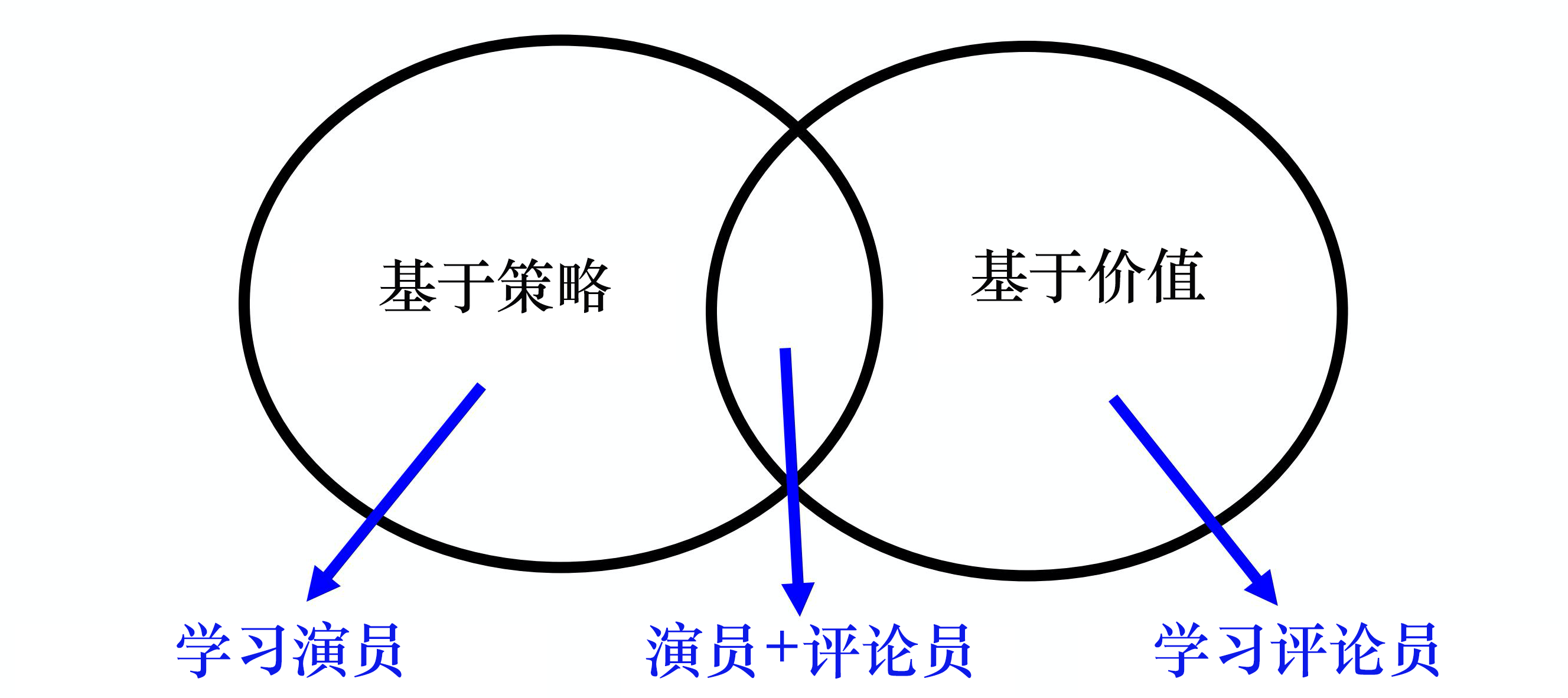
第 4 招就是不要用 DQN。用 DQN 处理连续动作还是比较麻烦。 基于策略的方法 PPO 和基于价值的方法 DQN,这两者其实是可以结合在一起的,如下图所示,也就是演员-评论员的方法。