Merge branch 'master' of github.com:datawhalechina/easy-rl
This commit is contained in:
qiwang067
@@ -80,7 +80,11 @@ PDF版本是全书初稿，人民邮电出版社的编辑老师们对初稿进
|
||||
| [第十三章 AlphaStar 论文解读](https://datawhalechina.github.io/easy-rl/#/chapter13/chapter13) | | |
|
||||
## 算法实战
|
||||
|
||||
[点击](https://github.com/johnjim0816/rl-tutorials)或者跳转```projects```文件夹下进入算法实战
|
||||
[点击](https://github.com/johnjim0816/rl-tutorials)或者网页点击```projects```文件夹进入算法实战
|
||||
|
||||
## 经典强化学习论文解读
|
||||
|
||||
[点击](https://github.com/datawhalechina/easy-rl/tree/master/papers)或者网页点击```papers```文件夹进入经典强化学习论文解读
|
||||
|
||||
## 贡献者
|
||||
|
||||
|
||||
@@ -77,19 +77,4 @@ for i_episode in range(1, cfg.max_episodes+1): # cfg.max_episodes为最大训练
|
||||
2. 由于本次环境为惯性系统，建议增加Ornstein-Uhlenbeck噪声提高探索率，可参考[知乎文章](https://zhuanlan.zhihu.com/p/96720878)
|
||||
3. 推荐多次试验保存rewards，然后使用searborn绘制，可参考[CSDN](https://blog.csdn.net/JohnJim0/article/details/106715402)
|
||||
|
||||
### 代码清单
|
||||
|
||||
**main.py**：保存强化学习基本接口，以及相应的超参数，可使用argparse
|
||||
|
||||
**model.py**：保存神经网络，比如全链接网络
|
||||
|
||||
**ddpg.py**: 保存算法模型，主要包含select_action和update两个函数
|
||||
|
||||
**memory.py**：保存Replay Buffer
|
||||
|
||||
**plot.py**：保存相关绘制函数
|
||||
|
||||
**noise.py**：保存噪声相关
|
||||
|
||||
[参考代码](https://github.com/datawhalechina/easy-rl/tree/master/codes/DDPG)
|
||||
|
||||
|
||||
@@ -64,20 +64,6 @@ for i_ep in range(cfg.train_eps): # train_eps: 训练的最大episodes数
|
||||
|
||||
|
||||
|
||||
## 主要代码清单
|
||||
|
||||
**main.py** 或 **task_train.py**：保存强化学习基本接口，以及相应的超参数
|
||||
|
||||
**agent.py**: 保存算法模型，主要包含choose_action(预测动作)和update两个函数，有时会多一个predict_action函数，此时choose_action使用了epsilon-greedy策略便于训练的探索，而测试时用predict_action单纯贪心地选择网络的值输出动作
|
||||
|
||||
**model.py**：保存神经网络，比如全连接网络等等，对于一些算法，分为Actor和Critic两个类
|
||||
|
||||
**memory.py**：保存replay buffer，根据算法的不同，replay buffer功能有所不同，因此会改写
|
||||
|
||||
**plot.py**：保存相关绘制函数
|
||||
|
||||
[参考代码](https://github.com/datawhalechina/easy-rl/tree/master/projects/codes/QLearning)
|
||||
|
||||
## 备注
|
||||
|
||||
* 注意 $\varepsilon$-greedy 策略的使用，以及相应的参数$\varepsilon$如何衰减
|
||||
|
||||
@@ -73,17 +73,3 @@ for i_episode in range(1, cfg.max_episodes+1): # cfg.max_episodes为最大训练
|
||||
也可以[tensorboard](https://pytorch.org/docs/stable/tensorboard.html)查看结果，如下：
|
||||
|
||||
|
||||
|
||||
### 代码清单
|
||||
|
||||
**main.py**：保存强化学习基本接口，以及相应的超参数，可使用argparse
|
||||
|
||||
**model.py**：保存神经网络，比如全链接网络
|
||||
|
||||
**dqn.py**: 保存算法模型，主要包含select_action和update两个函数
|
||||
|
||||
**memory.py**：保存Replay Buffer
|
||||
|
||||
**plot.py**：保存相关绘制函数，可选
|
||||
|
||||
[参考代码](https://github.com/datawhalechina/easy-rl/tree/master/codes/DQN)
|
||||
@@ -0,0 +1,238 @@
|
||||
# Deep Recurrent Q-Learning for Partially Observable MDPs（部分可观测马尔可夫决策过程的深度循环Q学习）
|
||||
作者：Matthew Hausknecht，Peter Stone <br>
|
||||
单位：Department of Computer Science The University of Texas at Austin <br>
|
||||
论文发表会议：National conference on artificial intelligence <br>
|
||||
论文发表时间：Submitted on 23 Jul 2015, last revised 11 Jan 2017 <br>
|
||||
论文查看网址：https://arxiv.org/abs/1507.06527
|
||||
|
||||
论文贡献：提出一种基于DQN的神经网络模型（DRQN），将包含卷积神经网络（CNN）的DQN模型和LSTM结合，使强化学习智能体拥有记忆力的特性。
|
||||
|
||||
## 一. 写作动机
|
||||
<font size="4">**Why:**</font> <br>
|
||||
在<font color="#660000"> *Playing Atari with Deep Reinforcement Learning(Mnih et al., 2013)* </font>中，DQN是使用智能体（Agent）遇到的包含当前状态的最后4个状态的组成（最后4个画面）作为**输入**。**目的**是获得画面中物体/角色的<font color="#0000dd">**方向**、**速度**</font>等信息。但换句话说，倘若遇到需要记忆特征超过四个画面的时间跨度任务时，对于DQN来说，则会由马尔可夫决策过程（MDP）变成部分可观测的马尔可夫决策过程（POMDP）。
|
||||
|
||||
<font size="4">**What:**</font> <br>
|
||||
部分可观测的马尔可夫决策过程（Partially-Observable Markov Decision Process, POMDP）是指：当前观测（Observation，obs）的不完整且带有噪音，不包含环境运作的所有状态。导致无法作为环境（Environment，env）的完整描述信息（智能体得到观测跟环境的状态不等价）。
|
||||
|
||||
<font size="4">**How:**</font> <br>
|
||||
论文作者提出，为避免因部分可观测的马尔可夫决策过程（POMDP）导致DQN在任务环境学习的过程中出现性能下降，引入**Deep Recurrent Q-Network (DRQN)**，是基于LSTM（Long Short-Term Memory，LSTM）和DQN的组合。并**证明使用DRQN能有效处理部分可观测的马尔可夫决策过程（POMDP）**，当评估智能体时，输入智能体的观测（obs）发生变化（遮盖、画面闪烁）时，因参数化价值函数（Value function）包含循环神经网络层（LSTM）能够使学习到的 策略$\pi_{\theta }$ 具有鲁棒性，不会发生策略崩塌。
|
||||
|
||||
## 二. 背景介绍
|
||||
### 1. Deep Q-Learning（深度Q学习）
|
||||
使用深度Q学习方法，是通过参数为$\theta$的深度神经网络来近似价值函数（Value Function）$V(s)$或动作价值函数（Action-Value Function）$Q(s,a)$来隐式的学习最优策略$\pi ^*$，输入环境的观测（obs），输出对观测（obs）估计的V值或Q值。
|
||||
|
||||
深度Q学习适用场景：连续状态空间（State space）离散动作空间（Action Space）任务。
|
||||
|
||||
价值函数的作用为：评估在当前状态-动作下，未来回报（Return）的期望。
|
||||
|
||||
使用深度神经网络作为强化学习的参数化值函数近似器的优点： <br>
|
||||
（1）具有深度学习自动提取特征的能力。 <br>
|
||||
（2）参数化模型将现有可见的观测（obs）泛化到没有见过的观测（obs）：$|\theta|\ll|S\times A|$ <br>
|
||||
（3）参数化模型可通过求导数的形式来更新神经网络模型参数。
|
||||
|
||||
参数化价值函数为：
|
||||
|
||||
$$V_\theta (s)\cong V^\pi (s) \\ Q_\theta (s,a)\cong Q^\pi (s,a)$$
|
||||
|
||||
深度Q学习保持学习稳定的技巧（Trick）： <br>
|
||||
（1）经验回放（Experience Replay）：针对数据层面的相关性和数据分布变化做改进，使得数据尽可能满足独立同分布（i.d.d）属性。 <br>
|
||||
（2）目标网络（Target Network）：解决在时序差分（Timing Difference，TD）学习时，TD target和当前Q网络高度相关的问题。
|
||||
|
||||
深度Q学习的损失函数（Loss Function）为：
|
||||
|
||||
$$\mathcal{L}_{i}\left(\theta_{i}\right)=\mathbb{E}_{\left(s, a, r, s^{\prime}\right) \sim \mathcal{D}}\left[\left(y_{i}-Q\left(s, a ; \theta_{i}\right)\right)^{2}\right] \\
|
||||
y_{i}=r+\gamma \max _{a^{\prime}} \hat{Q}\left(s^{\prime}, a^{\prime} ; \theta^{-}\right)
|
||||
$$
|
||||
深度Q学习的最优动作$a^*$为当前状态（state）下价值函数输出Q值最大对应的动作：
|
||||
$$
|
||||
a=arg\;\underset{a}{max} Q(s,a)
|
||||
$$
|
||||
### 2. Partial Observability（部分可观测）
|
||||
马尔可夫决策过程（MDP）五元组（S，A，P，$\gamma$，R）： <br>
|
||||
（1）S是状态的集合 <br>
|
||||
（2）A是动作的集合 <br>
|
||||
（3）$P(s'|s,a)$是环境的状态转移概率 <br>
|
||||
（4）$\gamma \in [0,1]$是对未来累积奖励（回报 Return）的折扣因子 <br>
|
||||
（5）R是奖励函数，R:S × A
|
||||
|
||||
部分可观测的马尔可夫决策过程（POMDP）七元组（S，A，P，$\gamma$，R，Ω，O）： <br>
|
||||
（1）Ω是观测$(obs,o)$的集合， $o\in \Omega$ <br>
|
||||
（2）O是观测函数，$O(s',a,o)= P(o | s',a)$
|
||||
|
||||
因为观测（obs）是对状态的部分描述，所以可能会遗漏一些信息。
|
||||
$$Q(o, a \mid \theta) \neq Q(s, a \mid \theta)$$
|
||||
|
||||
论文作者通过实验证明，使用DRQN可以缩小价值函数对于观测（obs）的Q值与对状态（State）的Q值之间的差距。即智能体学习到的策略能在具有POMDP性质的任务环境中具有鲁棒性。
|
||||
|
||||
## 三. 模型架构
|
||||
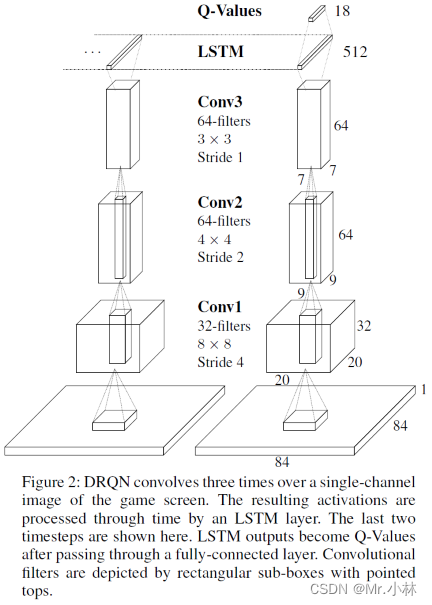 <br>
|
||||
**模型输入**：Atari 游戏的84*84像素的单通道图像 <br>
|
||||
**模型输出**：游戏对应18个离散动作的Q值
|
||||
|
||||
模型架构解释： <br>
|
||||
①首先使用3层卷积神经网络（Convolutional Neural Networks，CNN）提取图像特征。 <br>
|
||||
②其次传入LSTM，获得游戏画面之间的序列特征。 <br>
|
||||
③最后使用全连接层（Fully Connected Layers，FC）变成Q值。
|
||||
|
||||
## 四. 智能体更新方法
|
||||
**Bootstrapped Random Updates**：从经验池（Replay Memory）中随机选择一个回合的轨迹$\tau$ ，并从该回合的经验片段中随机选择开始点沿时间步骤顺序更新模型。（以时序差分Timing Difference的方式更新）
|
||||
|
||||
$$\tau =\left \{ s_0, a_0, s_1, r_1, a_1, \cdots ,s_{t-1}, r_{t-1}, a_{t-1}, s_t, r_t\right \} $$
|
||||
|
||||
例如：选择从轨迹$\tau$的$s_2$进行顺序更新，直到轨迹$\tau$的终止状态$s_t$停止。
|
||||
|
||||
设计缺陷：使用随机更新方式符合DQN中随机采样经验的更新策略。但在本论文的价值函数设计中包含LSTM层。导致在每次训练更新开始时，**LSTM**会因为 **隐含状态$h_{t-1}$** 的输入为零，导致LSTM难以学习比时间序列反向传播到达的时间步骤更长的时间范围。
|
||||
|
||||
**LSTM**结构图：
|
||||
|
||||
|
||||
|
||||
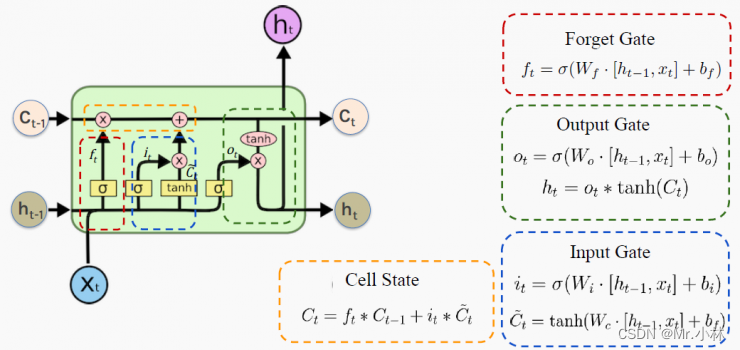
遗忘门（Forget Gate）：控制哪些数据保留，哪些数据要遗忘。 <br>
|
||||
输入门（Input Gate）：控制网络输入数据流入记忆单元的多少。 <br>
|
||||
输出门（Output Gate）：扛着记忆但与对当前输出数据的影响，即记忆单元中的哪一部分会在时间步t输出。 <br>
|
||||
细胞状态（Cell State）：将旧的细胞状态更新为当前细胞状态，由遗忘门和输入门共同控制。
|
||||
|
||||
本文使用的智能体的更新方式均为**随机更新策略**。
|
||||
|
||||
## 五. 任务环境
|
||||
本文选择9个Atari 2600游戏任务环境进行评估基于DRQN神经网络模型的智能体(Agent)性能。
|
||||
|
||||
游戏环境示意图为：
|
||||
|
||||
|
||||
|
||||
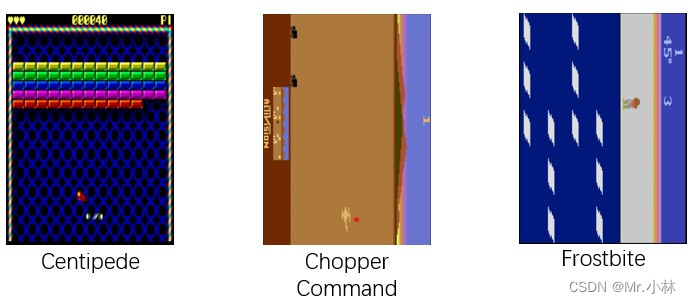
|游戏环境 | 介绍 |
|
||||
|--|--|
|
||||
|Asteroids |具有自然闪烁的NPC，使其成为潜在的循环学习候选 |
|
||||
| Ms Pacman | 通关类游戏，有闪烁的幽灵和强力药丸 |
|
||||
|Frostbite|平台类游戏|
|
||||
| Beam Rider | 射击类游戏 |
|
||||
| Centipede | 射击类游戏 |
|
||||
| Chopper Command | 射击类游戏 |
|
||||
|Ice Hockey|体育比赛类|
|
||||
|Double Dunk|体育比赛类|
|
||||
|Bowling|体育比赛类|
|
||||
|
||||
|
||||
- [Atari 2600在线游戏网页](https://www.free80sarcade.com/all2600games.php)
|
||||
|
||||
## 六. 损失函数与奖励函数
|
||||
**损失函数**（Loss Function）：论文作者主要提出基于DRQN的神经网络模型，没有对DQN的强化学习算法进行更改，仍然采用DQN的损失函数进行神经网络模型拟合（动作价值函数，Action-Value Function）。
|
||||
$$\mathcal{L}_{i}\left(\theta_{i}\right)=\mathbb{E}_{\left(s, a, r, s^{\prime}\right) \sim \mathcal{D}}\left[\left(y_{i}-Q\left(s, a ; \theta_{i}\right)\right)^{2}\right] \\
|
||||
y_{i}=r+\gamma \max _{a^{\prime}} \hat{Q}\left(s^{\prime}, a^{\prime} ; \theta^{-}\right)
|
||||
$$
|
||||
|
||||
**奖励函数**（Reward Function）：论文使用的任务环境为Atari 2600游戏环境，根据不同的游戏任务，环境都自带奖励函数，不需要额外定义。
|
||||
|
||||
## 七. 实验证明
|
||||
### 1. Flickering Pong POMDP（闪烁的Pong，部分可观测马尔可夫决策过程）
|
||||
DQN通过输入包含当前观测（obs）的最后四个画面来实现将部分可观测的马尔可夫决策过程（POMDP）转换成为马尔可夫决策过程（MDP）。
|
||||
|
||||
**实验目的**：而为了验证DRQN在具有POMDP性质的游戏环境中对连续的模糊输入具有鲁棒性。引入<font color="##00dd00"> **Flickering Pong POMDP** </font>对Pong游戏的修改。
|
||||
|
||||
|
||||
|
||||
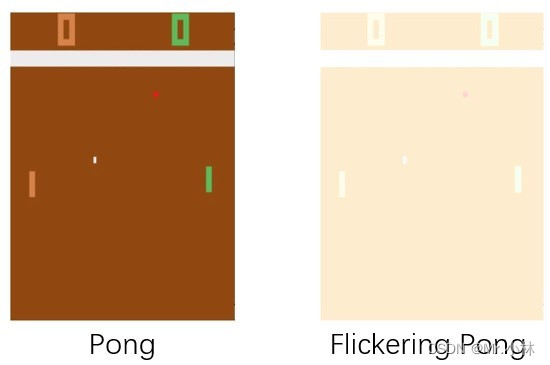
**实验设计**：在每个时间步长，游戏画面完全显示或完全模糊的概率 **$p=0.5$**。使用这种方式使 Flickering Pong 游戏环境 有一半的概率，画面被模糊化，使智能体得到观测（obs）具有POMDP性质。
|
||||
为了验证 ：
|
||||
①DQN神经网络模型中卷积层（CNN）能够具有在模糊观测画面中检测物体移动 **速度、方向** 的能力，在Flickering Pong游戏环境中输入包含当前观测画面的最后10个画面到模型中，并以可视化方式确认。
|
||||
②DRQN神经网络模型中LSTM层具有在模糊观测画面中检测物体历史特征，在Flickering Pong游戏环境中输入当前观测画面到模型中，并以可视化方式确认。
|
||||
|
||||
**实验baseline**：DQN神经网络模型（输入包含当前观测画面的**最后10个画面**）。
|
||||
|
||||
|
||||
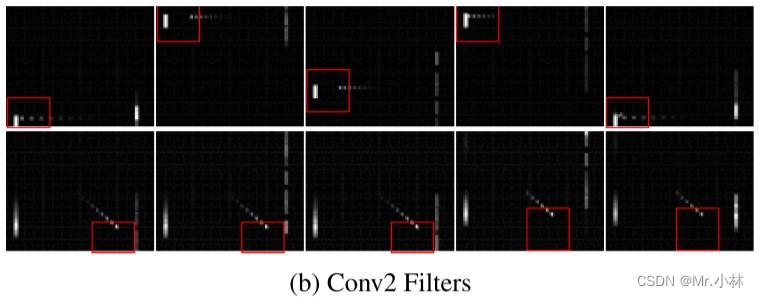
现象：在第一层卷积层中，滤波器主要检测到 Flickering Pong游戏环境 中的**球拍**。
|
||||
|
||||
|
||||
|
||||
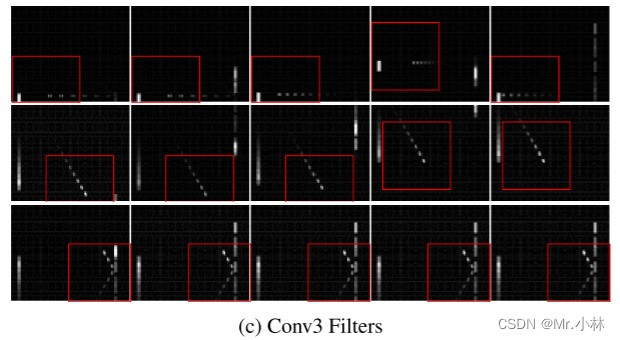
现象：在第二层卷积层中，滤波器开始检测到 Flickering Pong游戏环境 中的**球拍**以及**球**的运动方向，有的状态下滤波器也能同时检测到**球拍、球**。
|
||||
|
||||
|
||||
|
||||
现象：在第三层卷积层中，滤波器都能检测到**球拍**和**球**的相互作用，有偏转、球的速度和移动方向。
|
||||
|
||||
**实验**：为了验证DRQN神经网络模型中LSTM层能够检测到画面与画面间的序列特征，在每个时间步内仅输入当前观测（obs）到的**1个画面**到DRQN模型中。
|
||||
|
||||
|
||||
现象：LSTM层各单元能够透过具有闪烁的单个观测画面，检测到Flickering Pong游戏环境中的高级事件，例如**球从墙上反弹**等。
|
||||
|
||||
**实验结论**：通过 **输入10个连续观测画面到含有卷积层的DQN** 以及 **输入1个观测画面到含有LSTM层的DRQN** 进行对比，结果显示都能检测到游戏画面的历史特征。基于此，当任务环境具有POMDP性质时，上述两种方法都可供选择。证明**使用LSTM神经网络层，能够在具有时间序列特征的单个观测画面中整合序列特征**。
|
||||
|
||||
### 2. Evaluation on Standard Atari Games （标准的Atari游戏评估）
|
||||
**实验目的**：为了对比论文作者提出的DRQN神经网络模型和基于卷积神经网络（CNN）的DQN神经网络模型在标准的Atari 2600游戏任务环境中的表现，使用9个不同的 Atari 2600 游戏环境进行综合评估。
|
||||
|
||||
**实验设计**：为了让任务符合MDP性质，设置输入为包含当前观测画面的最后4个画面。并使用 **独立 t 检验** 计算得分的统计显著性，显著性水平$P=0.05$
|
||||
|
||||
**实验baseline**：基于卷积神经网络（CNN）的DQN神经网络模型在9个标准的Atari 2600游戏任务环境中的表现。
|
||||
|
||||
|
||||
|
||||
**实验结论1**：在9个不同的游戏任务环境中，基于DRQN神经网络模型的智能体得分在5个环境上的表现优于基于DQN神经网络模型的智能体。
|
||||
|
||||
|
||||
|
||||
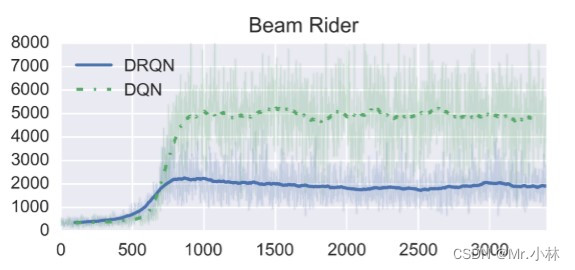
**实验结论2**：DRQN在Beam Rider游戏中表现相比DQN明显更差。
|
||||
|
||||
<font color="#dd00dd">*个人分析*</font> ：可能是Beam Rider游戏中的**决策依据**并不需要时间跨度太久远的观测画面特征，主要依于当前即时观测画面的特征。加入的LSTM层反而导入过多不必要的特征造成智能体决策上的干扰。
|
||||
|
||||
|
||||
|
||||
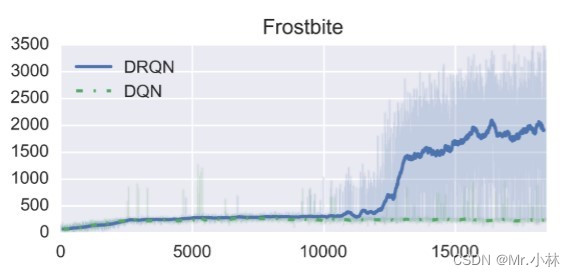
**实验结论3**：DRQN在 Frostbite游戏 中表现最好。游戏的任务是要求玩家跳过所有四排移动的冰山并返回屏幕顶部。多次穿越冰山后，已经收集到足够的冰块，可以在屏幕右上角建造一个冰屋。随后玩家可以进入冰屋进入下一关。
|
||||
|
||||
<font color="#dd00dd">*个人分析*</font>： Frostbite游戏任务 具有长时间跨度决策性质，因此DRQN的LSTM层能够学习到具有长时间跨度的特征，智能体决策上的依据能够超越输入模型的4个观测画面所具有的特征。
|
||||
|
||||
### 3. MDP to POMDP Generalization（MDP到POMDP的泛化性）
|
||||
**实验目的**：为了评估使用基于DRQN模型的智能体在标准的MDP（输入为包含当前观测画面的最后4个画面）上训练得到的策略$\pi$，在推广到POMDP性质的相同游戏任务环境时，智能体的策略$\pi$能否保持有效性？
|
||||
|
||||
**实验设计**：选择用实验2的9个Atari 2600游戏任务环境进行闪烁（Flickering）设置，在每个时间步长，游戏画面完全显示的概率$p$按照0.1~0.9的概率依次使用训练好的智能体进行实验。
|
||||
|
||||
**实验baseline**：基于卷积神经网络（CNN）的DQN神经网络模型在POMDP性质的Atari 2600 游戏任务环境中的百分比原始分数（Percentage Original Score）。
|
||||
|
||||
|
||||
|
||||
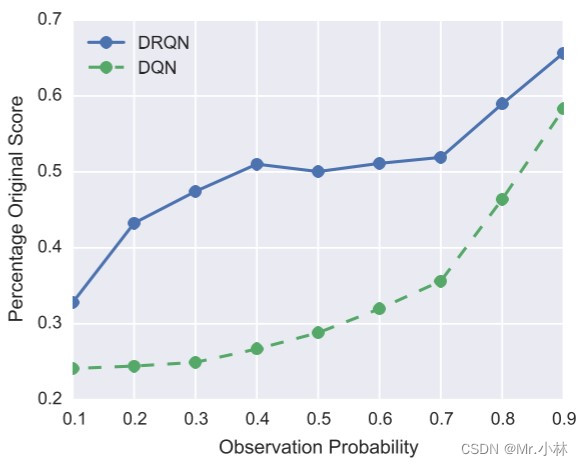
**实验结论**：在标准的MDP训练的基于DRQN模型的智能体和基于DQN模型的智能体，分别在闪烁（Flickering）设置的游戏环境中进行评估，通过折线图观察到，基于DRQN模型的智能体性能下降的幅度相比基于DQN模型的智能体更小。
|
||||
$$Percentage\,Original\,Score=\frac{ {\textstyle \sum_{i=1}^{9}}POMDP\,Score }{ {\textstyle \sum_{i=1}^{9}}MDP\,Score } \\
|
||||
i\ is\ the\ number\ of\ game\ environments$$
|
||||
|
||||
## 八. 相关工作
|
||||
### 1. LSTM在解决具有POMDP性质的任务上相比于RNN的优越性
|
||||
在<font color="#660000"> *Reinforcement learning with long shortterm memory(Bakker et al., 2001)* </font>这篇论文中，在具有POMDP性质的Corridor和Cartpole环境上，使用LSTM神经网络作为强化学习中的 优势函数（Advantage Function）近似，相比于使用RNN神经网络能够更好的完成任务。虽然Corridor和Cartpole环境的状态空间特征数量以及动作空间，相比于Atari 2600 游戏环境都很少！
|
||||
|
||||
### 2. LSTM在解决具有POMDP性质的任务框架
|
||||
在<font color="#660000"> *Solving deep memory POMDPs with recurrent policy gradients(Wierstra et al., 2007)* </font>这篇论文首先使用策略梯度（Policy Gradient）结合LSTM神经网络解决具有POMDP性质的问题。但模型在特征提取上属于手工设计的特征，并没有结合深度神经网络模型做到自动提取特征。
|
||||
|
||||
## 九. 结论
|
||||
1. 基于DRQN模型的智能体在 POMDP性质的 Atari 2600 游戏环境下处理观测（obs）时，能够利用单个观测画面的输入，达到与基于DQN模型的智能体在输入连续10个观测画面得到的历史特征相同。即使用基于DRQN模型能够降低计算复杂度。
|
||||
2. 根据 标准的 Atari 2600 游戏环境的任务属性不同，在需要接收长时间跨度特征的任务中（例如 Frostbite 游戏），基于DRQN模型的智能体的表现会远超于基于DQN模型的智能体。
|
||||
3. 基于DRQN模型的智能体在相同的 Atari 2600 游戏环境下遇到出现POMDP的情况下，其泛化性会比基于DRQN模型的智能体好。
|
||||
|
||||
## 十. 贡献
|
||||
本文通过实验证明，加入 **LSTM神经网络** 的DRQN模型的智能体，面对具有POMDP性质的问题上，其性能表现优于DQN。但在实践过程中，仍需以任务的实际情况而定。通用性不高，并无法带来系统性的提升。
|
||||
|
||||
## 十一. 下一步的工作
|
||||
### 1. 强化学习算法层面
|
||||
在连续状态空间、离散动作空间的任务中，有结合**Double DQN**和**Dueling DQN**的**D3QN算法**。可以在本论文提出的DRQN神经网络模型架构上，使用D3QN强化学习算法来进行实验，观察智能体在本次论文的实验中表现不好的任务环境（例如 Beam Rider 游戏）是否能够得到性能上的提高，并达到系统性的提升。
|
||||
|
||||
### 2. 任务环境层面
|
||||
在强化学习机器控制领域上的任务情境中，智能体不仅需要对环境输出的观测（obs）学习时间序列特征，还需要将智能体本身输出的动作（Action）纳入成为观测的一部分进行学习。期待之后智能体训练好的 **策略$\pi$** 既能够对环境输出的观测进行考量，也能将历史动作纳入考虑的范围，以输出连贯合理的决策动作。
|
||||
|
||||
|
||||
### 3. 深度神经网络模型层面
|
||||
随着自注意力机制为核心的Transformer神经网络模型的出现，Transformer抛弃传统的CNN和RNN，只使用注意力机制（Attention）。同时Vision Transformer的出现打破了NLP领域和CV领域的边界，以Transformer为代表的决策模型成为当前RL领域的新范式。
|
||||
那么是否在同样是以图像作为观测的 Atari 2600 游戏任务环境上，以DQN算法为基础，使用 **基于Vision Transformer模型** 拟合价值函数，来隐式的学习策略$\pi$，以期望在智能体能够达到更好的性能！
|
||||
|
||||
|
||||
## 参考文献
|
||||
1. Volodymyr Mnih, J. et al. 2013. Playing Atari with Deep Reinforcement Learning.
|
||||
2. Wierstra, D.; Foerster, A.; Peters, J.; and Schmidthuber, J. 2007. Solving deep memory POMDPs with recurrent policy gradients.
|
||||
3. Bakker, B. 2001. Reinforcement learning with long shortterm memory. In NIPS, 1475–1482. MIT Press.
|
||||
4. [推荐中的序列化建模：Session-based neural recommendation](https://zhuanlan.zhihu.com/p/30720579)
|
||||
5. [论文十问-快速理解论文主旨的框架](https://www.cnblogs.com/xuyaowen/p/raad-paper.html)
|
||||
6. [RLChina 2022 强化学习暑期课](http://rlchina.org/topic/491)
|
||||
7. [蘑菇书EasyRL](https://github.com/datawhalechina/easy-rl)
|
||||
|
||||
====================================<br>
|
||||
作者：林俊杰<br>
|
||||
研究单位：台湾成功大学制造资讯与系统研究所<br>
|
||||
研究方向：强化学习、深度学习<br>
|
||||
联系邮箱：554317150@qq.com
|
||||
|
||||
224
papers/DQN/Deep Reinforcement Learning with Double Q-learning.md
Normal file
224
papers/DQN/Deep Reinforcement Learning with Double Q-learning.md
Normal file
@@ -0,0 +1,224 @@
|
||||
# Deep Reinforcement Learning with Double Q-Learning 论文剖析
|
||||
|
||||
Hado van Hasselt 、Arthur Guez 、 David Silver from Google DeepMind
|
||||
|
||||
## 〇. 文章信息
|
||||
|
||||
**Deep Reinforcement Learning with Double Q-learning**
|
||||
|
||||
作者：Hado van Hasselt 、Arthur Guez 、 David Silver from Google DeepMind ,2015
|
||||
|
||||
https://arxiv.org/abs/1509.06461
|
||||
|
||||
|
||||
|
||||
## 一. 写作动机
|
||||
|
||||
高估问题（overestimation）一直是强化学习中存在的问题，但是一直以来其来源有多种说法，一是归因于不灵活的函数近似（Thrun和Schwartz, 1993），一是来自噪声（van Hasselt, 2010, 2011）。通过实验也表明，高估问题的普遍性相较之前认识的要普遍的多，需要找到方法缓解其影响。
|
||||
|
||||
本文的写作动机就是探索高估的产生，验证高估问题对于Q-Learning是否不利，并寻找缓解高估问题的方法。
|
||||
|
||||
|
||||
|
||||
## 二 . Q-Learning算法的进化历史
|
||||
|
||||
本文中，作者总结了DQN的发展：
|
||||
|
||||
### 1. Q-Learning——解决时序决策问题的方法
|
||||
|
||||
Q-Learning是一种**时序差分方法**，很好的被用在时序决策问题中(Watkins, 1989)，其通过估计最优动作价值函数$$ Q_{\pi}(s,a)=\mathbb{E}[R_1+\gamma R_2+...|S_0=s, A_0=a,\pi],$$ 并对每个状态选择最优的动作价值函数所对应的动作，从而间接生成最优策略。
|
||||
|
||||
具体请参考Q-Learning文章，此处给出迭代公式方便后续说明。
|
||||
|
||||
$$ Q(S_t,A_t)=Q(S_t,A_t)+ \alpha (Y_t^Q-Q(S_t,A_t)) \tag{1} $$
|
||||
|
||||
### 2. 价值函数拟合的Q-Learning
|
||||
|
||||
因为状态过多或者连续，无法遍历所有状态，需要使用参数化函数$ Q(s,a;\theta _t)$对现有值进行拟合，并对未知状态的价值函数进行预测，通过公式
|
||||
|
||||
$$\theta_{t-1}=\theta_t +\alpha(Y_t^Q-Q(S_t,A_t;\theta_t))\nabla Q(S_t, A_t,;\theta _t) \tag{2} $$
|
||||
|
||||
完成参数更新，其中$Y_t^Q =R_{t+1}+\gamma \substack{max\\a}Q(S_{t+1},a;\theta _t)$是TD-target, 主要思想就是使用类似梯度下降的方法，使得拟合出的参数化函数更加接近目标，也就是说更加符合真实值。
|
||||
|
||||
解决了传统Q-Learning中的无法解决的**未知状态**问题，即欠鲁棒的问题。
|
||||
|
||||
### 3.Deep Q Networks（DQN）
|
||||
|
||||
（Mnih et al. ,2015)）——神经网络+Q-Learning
|
||||
|
||||
说到函数拟合就不得不提到神经网络，它具有极强的**函数拟合**能力，DQN应运而生。
|
||||
|
||||
DQN针对传统Q-Learning有以下三点改进，提高了算法的性能：
|
||||
|
||||
1. #### 使用神经网络来代替参数化函数,增强了函数拟合能力
|
||||
|
||||
2. #### 使用目标网络
|
||||
|
||||
使用一个异步更新的目标网络,网络参数用$\theta^-$表示（每$\tau$次将Q-net的参数$\theta$赋值给目标网络）用来进行目标的计算。
|
||||
|
||||
$$Y_t^Q = R_{t+1}+\gamma\substack{max\\a}Q(S_t=s, A_t=a;\theta^-_t) \tag{3} $$
|
||||
|
||||
|
||||
|
||||
3. #### 使用**经验回放**(Lin, 1992)：储存经验并重复使用，增加了利用率，减少采样成本
|
||||
|
||||
4. #### Double DQN
|
||||
|
||||
本文的重点，下一章介绍
|
||||
|
||||
|
||||
|
||||
## 三 . Double DQN
|
||||
|
||||
### 1. 具体操作
|
||||
|
||||
更换计算目标的方式，公式为：
|
||||
|
||||
$$Y_t^Q = R_{t+1}+\gamma Q(S_t=s, A_t=\substack{argmax\\{a \in \mathbb{A}}}Q(s,a|\theta_t^-);\theta_t) \tag{4} $$
|
||||
|
||||
### 2. 思想来源：解耦选取与计算
|
||||
|
||||
在传统DQN中,TD-target的计算可以分为两个步骤：**最优动作的选取** 与 **最优动作价值函数的计算** 。该公式可以变形为以下分解形式:
|
||||
|
||||
$$ a^*=\substack{argmax\\{a \in \mathbb{A}}}Q(s,a|\theta_t)\\Y_t^Q=r+\gamma Q(S_t=s, A_t=a^*;\theta_t)$$
|
||||
|
||||
计算目标的任务就转换到了目标网络上：
|
||||
|
||||
$$
|
||||
a^*=\substack{argmax\\{a \in \mathbb{A}}}Q(s,a|\theta_t^-)\\Y_t^Q=r+\gamma Q(S_t=s, A_t=a^*;\theta_t^-)
|
||||
$$
|
||||
使用上面提到的Double Q-Learning，则变为以下形式：
|
||||
|
||||
$$ a^*=\substack{argmax\\{a \in \mathbb{A}}}Q(s,a|\theta_t^-)\\Y_t^Q=r+\gamma Q(S_t=s, A_t=a^*;\theta_t)$$
|
||||
|
||||
***其实Q-Learning也有Double的形式，分别训练两个模型$\theta$,$\theta'$ 操作一样，只是这里Double DQN巧妙地使用了目标网络$\theta^-$ 作为第二个网络***
|
||||
|
||||
为了方便观看，使用表格形式展示
|
||||
|
||||
| | DQN | DQN+target network | Double DQN |
|
||||
| :--------------------: | :--------------: | :----------------: | :----------------: |
|
||||
| 最优动作的选取 | 策略网络$\theta$ | 目标网络$\theta^-$ | 目标网络$\theta^-$ |
|
||||
| 最优动作价值函数的计算 | 策略网络$\theta$ | 目标网络$\theta^-$ | 策略网络$\theta$ |
|
||||
|
||||
由此可以看出如何解耦，在传统的DQN+目标网络的方法上，最优动作的选取 与 最优动作价值函数的计算 两步是耦合的，但是Double DQN解耦二者，达到了缓解高估的效果。至于为什么要这么做，就需要清晰的了解高估问题是如何产生的，作者在下一部分明确的证明了高估现象的发生与高估的上下限，并使用实验验证了理论。
|
||||
|
||||
|
||||
|
||||
## 四. 高估问题
|
||||
|
||||
本文另一贡献就是系统的分析了高估问题产生的原因和如何影响了Q-Learning。
|
||||
|
||||
### 1. 理论推导
|
||||
|
||||
#### (1) 为什么会产生高估？
|
||||
|
||||
简单来说，因为神经网络等估计方法存在误差，导致估计出的在某一固定状态$s$下，不同动作的动作价值函数$Q(A_t=a_i, S_t=s)$相对真实值$Q_*(A_t=a_i, S_t=s)$估计误差。假设估计噪声为高斯，无偏均值为0，误差可正可负，到此并无大碍，但是接下来的更新时的操作计算TD-target的时候，如公式$(3)$，使用了max操作，这导致在这一步的误差始终为正的，造成正的偏差，这就是导致高估的原因。
|
||||
|
||||
举个形象生动的例子：每天食堂拿盒饭，每盒的量500g大致相等，但是有的稍多为530g，有的稍少为470g。你每天随机选择一盒作为午餐，一个月下来你的体重没有变化，因为吃到的盒饭期望是每盒的平均值500g。但是第二个月你通过灵敏的视觉，每天都挑最多的那一盒，一个月下来胖了三斤，因为这时候吃到盒饭的期望为最大值530g。
|
||||
|
||||
选择最多的盒饭的过程就是max操作，你吃进去的饭通过公式$(1)$消化（更新），更新了你的体重，也就是动作价值函数的估值。
|
||||
|
||||
#### (2) 高估指标的理论推导
|
||||
|
||||
Thrun and Schwartz (1993)首先发现了高估的现象，表明如果动作值包含均匀分布在区间$[-\epsilon,\epsilon]$中的随机误差，则每个目标被高估到上限 $\gamma \in \frac{m-1}{m+1}$ ，其中 m 是动作的数量。
|
||||
|
||||
由贝尔曼最优方程可以得出最优动作价值函数与最优状态价值函数之间的关系：
|
||||
|
||||
$$Q_*(s,a)=V_*(s) \tag{5} $$
|
||||
|
||||
因为环境固定，奖励固定时，状态价值函数为常量，假设：任意动作价值函数的无偏估计值为$Q_t(s,a)$，则有等式$(6)$成立
|
||||
|
||||
$$ \sum_a (Q_t(s,a)-V_*(s))=0 \tag{6} $$
|
||||
|
||||
即使定义估计是无偏的，平均误差为零，但不是每个估计的误差均为零，也会有以下情况的产生：
|
||||
|
||||
$$\frac{1}{m} \sum_a(Q_t(s,a)-V_*(s))^2=C (m>1为动作个数，C>0为实数) \tag{7} $$
|
||||
|
||||
在这种假设下，使用$(3)$中的max操作，利用$(2)$进行价值函数的更新时，$max_aQ_t(s,a) \geq V_*(s)+ \sqrt{\frac{C}{m-1}}$ ,得到了高估的下限。
|
||||
|
||||
文中特意提到，Double Q-Learning的高估下限为0。
|
||||
|
||||
证明可以参考原文附录，很详细，在此不赘述。
|
||||
|
||||
#### (3) 为什么Double DQN可以解决高估？
|
||||
|
||||
接着盒饭说。此时你感觉自己有点胖，命令你的室友替你拿盒饭，无论你的室友怎样拿，肯定不会比你自己拿的时候（挑最重的拿）多，即$Q(s,a_*;\theta^-) \leq \substack{max\\a}Q(s,a)$，也就减少了目标的高估影响，从而减少了对动作价值函数的估计。
|
||||
|
||||
|
||||
|
||||
### 2. 实验
|
||||
|
||||
本文共做两次实验验证以上理论推导
|
||||
|
||||
#### 实验一：验证Q-Learning与Double Q-Learning在价值函数估计上的性能比较
|
||||
|
||||
|
||||
|
||||
作者实验证明，上图中横坐标为动作数，纵坐标为估计的Q值与最优值的误差（重复100次取平均），橙色为Q-learning，蓝色为Double Q-learning，可以看出随着动作数增加，Q-learning误差逐渐增大，而Double Q-learning基本无偏。
|
||||
|
||||
|
||||
|
||||
#### 实验二：通过参数拟合对比试验验证高估来源，并验证Double Q-Learning能有效缓解高估问题
|
||||
|
||||
|
||||
|
||||
证明了Double Q-learning能够减少过拟合后，作者做了三组实验**模仿参数拟合**，以验证高估产生。
|
||||
|
||||
图表中横坐标为状态，共有13个状态，纵坐标为Q值的大小。共有十个动作。
|
||||
|
||||
- 左列中，紫色的线代表每个状态真实的最优Q值，绿线为动作价值函数的真实值，绿点为真实的不包含噪声的采样点。动作仅仅在13个状态中的11上采样，在未采样点上观察情况。第一行和第二行实验使用6阶多项式去拟合，第三行实验使用9阶多项式。可以看出左图第二行在采样点上的逼近也不精确，是由于多项式阶数低不够灵活；左图第三行可以看出，虽然在采样点上逼近都很好，但在未采样的的地方误差很大，过拟合。
|
||||
- 中列三行图，每幅图中10条绿线是10个动作分别对应的动作值函数，虚线是每个状态下最大动作值。可以看出**最大动作值基本都比左边图中的真实最优Q值大**，当我们使用这些动作价值函数的估计进行Q-Learning的更新时，**使用公式$(2)$ 中$max_aQ_t(s,a) $, 高估现象产生**。
|
||||
- 右列三行图，橙线是中间图中黑色虚线与左边图中紫线作差的结果，即高估，蓝线是使用了Double Q-Learning的估计效果，蓝线的平均值更接近0，这表明**Double Q-Learning确实可以减少Q-Learning在函数逼近中的高估问题**。
|
||||
|
||||
通过实验，发现不够灵活的函数逼近对Q值的估计不精确，但是**足够灵活的函数逼近在未知状态中会产生更大误差**，**导致更高的高估**，DQN就是一种非常灵活的函数逼近，使用了神经网络来逼近价值函数。而高估最终会阻止学习到最优策略，作者后面也通过Atari上的实验证明了这点，且通过Double Q-Learning减少高估最终策略也会得到改善。
|
||||
|
||||
### 3.高估如何影响DQN？
|
||||
|
||||
选择是相对的，均匀的高估不会对动作的选择造成影响。
|
||||
|
||||
真正造成影响的是：高估是非均匀的，回到吃盒饭的例子。你和我有一样的体质（吃-涨的比例相同），我比你稍微重，我们每次都只拿最多的盒饭530g，一个月涨的体重都一样，一个月之后还是我比你稍微重。但是你吃的是A种盒饭，我吃的是B种盒饭，这就会导致非均匀高估，导致你可能长胖更快一点，一个月之后甚至超过我，**导致次最优解**。
|
||||
|
||||
重要的事情说三遍：**均匀高估无影响，真正产生影响的是非均匀高估**，此后将高估一词指代非均匀高估。
|
||||
|
||||
## 五. 基于Atari2006的实验
|
||||
|
||||
### 1. 训练细节
|
||||
|
||||
网络架构是一个卷积神经网络（Fukushima, 1988; LeCun et al., 1998），具有 3 个卷积层和一个全连接隐藏层（总共大约 150 万个参数）。网络将最后四帧作为输入，输出每个动作的动作值。在每场游戏中，网络都在单个 GPU 上训练 200M 帧，或大约 1 周。
|
||||
|
||||
### 2.实验结果
|
||||
|
||||
|
||||
|
||||
作者在6款游戏上重复进行实验，得出以下结果
|
||||
|
||||
- 1， 2行展示了六款游戏的真实价值与估计价值，蓝色为DoubleDQN,红色为DQN。肉眼可见，DoubleDQN的价值拟合更趋近于真实值，相比DQN高估现象减弱明显。并且其中两家款游戏的高估十分严重。
|
||||
- 选择高估现象作为严重的两款游戏（中下），展示其训练期间的得分情况：当高估开始时分数下降，证明了高估现象可以影响算法性能。使用 Double DQN 学习更加稳定。
|
||||
|
||||
最后，为了证明算法的稳定性，采用了不同的时间点开始切入学习（让人先玩一段时间，智能体再接手），发现DDQN的结果更加稳定，并且DDQN的解并没有利用到环境的相关特性。
|
||||
|
||||
##### 注：更多的实验结果篇幅原因这里不再做更多实验展示
|
||||
|
||||
|
||||
|
||||
## 六.本文的贡献
|
||||
|
||||
这篇论文有五个贡献。
|
||||
|
||||
- 首先，展示了为什么 Q-Learning存在高估的问题。
|
||||
- 其次，通过分析 Atari 游戏的价值估计，发现这些高估在实践中比之前认为的更为普遍和严重。
|
||||
- 第三，证明可以使用Double Q-Learning 学习有效地减少高估，从而使学习更加稳定和可靠。
|
||||
- 第四，提出了一种Double DQN具体实现，它使用 DQN 算法的现有架构和深度神经网络，无需额外的网络或参数。
|
||||
- 最后，展示了 Double DQN 找到了更好的策略，在 Atari 2600 域上获得了当时最优的结果。
|
||||
|
||||
## 七.作者介绍
|
||||
|
||||
于天琪，男，20多岁，单身，就读于哈尔滨工程大学陈赓实验班\
|
||||
知乎主页：https://www.zhihu.com/people/Yutianqi \
|
||||
qq:2206422122 \
|
||||
欢迎交流，互相学习
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
176
papers/DQN/Dueling Network Architectures for Deep Reinforceme.md
Normal file
176
papers/DQN/Dueling Network Architectures for Deep Reinforceme.md
Normal file
@@ -0,0 +1,176 @@
|
||||
# Dueling Network Architectures for Deep Reinforcement Learning
|
||||
|
||||
## 〇. 文章信息
|
||||
|
||||
**Dueling Network Architectures for Deep Reinforcement Learning**
|
||||
|
||||
Ziyu Wang、Tom Schaul、Matteo Hessel、Hado van Hasselt、Marc Lanctot、Nando de Freitas
|
||||
|
||||
Google DeepMind
|
||||
|
||||
[https://arxiv.org/abs/1511.06581](https://arxiv.org/abs/1511.06581 "https://arxiv.org/abs/1511.06581")
|
||||
|
||||
## **一、写作动机**
|
||||
|
||||
Dueling DQN出现以前，基于深度学习RL的大多数方法都是用标准的神经网络结构，如MLP、LSTM等。此类工作的重点是改进控制和RL算法，或将现有的神经网络架构推广到RL中。
|
||||
|
||||
本文旨在提出一种适用于Model-free的RL算法的神经网络结构，该结构具有很好地灵活性和互补性。
|
||||
|
||||
## **二、** 预备知识
|
||||
|
||||
 若 $s_t$是智能体感知到的由 $M$个图像帧组成的视频，则有：
|
||||
|
||||
$$
|
||||
s_t = (x_{t−M+1},\cdots,x_t)\in S
|
||||
$$
|
||||
|
||||
与之对应的，$a_t$是智能体备选动作的离散集，则 $a_t \in A={1,2,3,\cdots,|A|}$； 游戏模拟器产生的奖励信号则为 $r_t$。智能体的目标是最大化折扣汇报 $R_t$( $R_t= \sum _{r=t}^\infty \gamma^{r-t}r_t$)，在这个公式中， $\gamma\in[0,1]$是折扣因子，它权衡了即时和未来奖励的重要性。
|
||||
|
||||
对于根据随机策略 $\pi$ 行动的智能体，其状态-动作对$(s, a)$ 和状态 $s$ 的值定义如下：
|
||||
|
||||
$Q^{\pi}(s,a) = E[R_{t}|s_{t}=s,a_{t}=a,\pi]$（动作价值函数）
|
||||
|
||||
$V^{\pi}(s) = E_{a \sim \pi(s)}[Q^{\pi}(s,a)]$（状态价值函数）
|
||||
|
||||
  $Q^{\star}(s, a) = \mathop{max}\limits_{\pi} Q^\pi(s, a)$（最优动作价值函数）
|
||||
|
||||
$V^{\star}(s)=\mathop{max}\limits_{\pi}V^{\pi}(s)$（最优状态价值函数）
|
||||
|
||||
  $A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s,a)$（优势函数）
|
||||
|
||||
**Theorem 1：**$V^{\star}(s) = \mathop{max}\limits_{a} Q^{\star}(s, a)$ （最优价值优势函数等于最优动作价值函数关于动作 $a$的最大值）
|
||||
$$
|
||||
A^{\star}(s, a)=Q^{\star}(s, a)-V^{\star}(s).（同时对左右两边关于动作a求最大值）
|
||||
$$
|
||||
|
||||
$$
|
||||
\mathop{max}\limits_{a}A^{\star}(s, a)=\mathop{max}\limits_{a}Q^{\star}(s, a)-V^{\star}(s)
|
||||
$$
|
||||
|
||||
$$
|
||||
\mathop{max}\limits_{a}A^{\star}(s, a) = \mathop{max}\limits_{a}Q^{\star}(s, a) - \mathop{max}\limits_{a}Q^{\star}(s, a) =0
|
||||
$$
|
||||
|
||||
另外有：
|
||||
|
||||
$$
|
||||
A^{\star}(s, a)=Q^{\star}(s, a)-V^{\star}(s) \Rightarrow Q^{\star}(s, a)=A^{\star}(s, a)+V^{\star}(s)
|
||||
$$
|
||||
|
||||
$$
|
||||
Q^{\star}(s, a)=A^{\star}(s, a)+V^{\star}(s) \Rightarrow Q^{\star}(s, a)=A^{\star}(s, a)+V^{\star}(s)-0
|
||||
$$
|
||||
|
||||
$$
|
||||
A^{\star}(s, a)+V^{\star}(s)+0 = A^{\star}(s, a)+V^{\star}(s)-\mathop{max}\limits_{a}A^{\star}(s, a)
|
||||
$$
|
||||
|
||||
**Theorem 2：** $Q^{\star}(s, a)=A^{\star}(s, a)+V^{\star}(s)-\mathop{max}\limits_{a}A^{\star}(s, a)$
|
||||
|
||||
### 2.1 Deep Q-networks
|
||||
|
||||
$Q(s, a; θ)$是神经网络对 $Q^{\star}(s, a)$的近似，神经网络的输入为状态 $s$，通过神经网络将输入映射到一个输出向量中，输出向量为 $s$状态下对每一个动作$a$的打分。
|
||||
|
||||
迭代$i$处的损失函数:
|
||||
|
||||
$$
|
||||
L_i(\theta_i)=E_{s,a,r,s'}[(y_i^{DQN}-Q(s,a;\theta_i))^2]
|
||||
$$
|
||||
|
||||
其中，$y^{DDQN}{i}=r+\gamma Q(s'+ \mathop{max}\limits_{a'}Q(s',a';\theta^{-}))$。
|
||||
|
||||
另外，还可以从梯度下降和经验回放的角度对训练的方式进行修改。
|
||||
|
||||
* 梯度下降
|
||||
|
||||
$$
|
||||
\nabla_{\theta_i} L_i(\theta_i)=E_{s,a,r,s'}[(y_i^{DQN}-Q(s,a;\theta_i))\nabla_{\theta_i}Q(s,a;\theta_i)]
|
||||
$$
|
||||
|
||||
* 经验回放
|
||||
|
||||
$$
|
||||
L_i(\theta_i) = E_{s,a,r,s'} \sim u(D)[y_i^{DQN}-Q(s,a;\theta_i))^2]
|
||||
$$
|
||||
|
||||
在学习过程中，智能体积累了一个数据集 $D_t = {e_1, e_2, . . . , e_t}$，其中经验$e_t = (s_t, a_t, r_t, s_{t+1})$ 来自许多回合。
|
||||
|
||||
### 2.2 Double Deep Q-networks
|
||||
|
||||
$$
|
||||
y^{DDQN}_{i}=r+\gamma Q(s'+ argmax_{a'}Q(s',a';\theta_{i};\theta^{-}))
|
||||
$$
|
||||
|
||||
DDQN与DQN基本一致，只是改变了 $y^{DDQN}_{i}$的表达式。
|
||||
|
||||
## **三、Dueling Network**的架构
|
||||
|
||||
与DQN不同，Dueling Network近似的是 $A^{\star}(s, a)$和 $V^{\star}(s)$，分别为 $A(s,a;\theta,\alpha)$和 $V(s;\theta,\beta)$。这也就意味着，Dueling Network可以使用同一个卷积网络的参数来提取特征，但输出则使用不同的结构。
|
||||
|
||||
|
||||
|
||||
具体地说，根据**Theorem 2**，有：
|
||||
|
||||
$$
|
||||
Q(s, a; \theta, \alpha, \beta) = V (s; \theta, \beta) + A(s, a; \theta, \alpha)-\mathop{max}\limits_{a}A(s, a; \theta, \alpha)
|
||||
$$
|
||||
|
||||
由于Dueling Network只是改变了网络的架构，所以训练网络的方法与DQN和DDQN一致，所有基于DQN的训练改进都可以用在Dueling Network上面。
|
||||
|
||||
### 3.1 $\mathop{max}\limits_{a}A(s, a; θ, α)$ 的作用
|
||||
|
||||
因为 $Q^{\star}(s, a)=A^{\star}(s, a)+V^{\star}(s)$，所以利用这种方式得到的 $Q^{\star}(s, a)$不唯一。
|
||||
|
||||
若同时给$A^\star$增一个数字，给$V^\star$减少相同的数字，则会得到与之前相同的$Q^{\star}(s, a)$。而增加 $\mathop{max}\limits_{a}A(s, a; θ, α)$一项后就不会出现这种情况。
|
||||
|
||||
### 3.2 实际使用中的 $\mathop{max}\limits_{a}A(s, a; θ, α)$
|
||||
|
||||
在实际的使用中，往往 $Q(s, a; \theta, \alpha, \beta)$中的第三项不使用$\mathop{max}\limits_{a}A(s, a; \theta, \alpha)$，而使用平均值，即：
|
||||
|
||||
$$
|
||||
Q(s, a; \theta, \alpha, \beta) = V (s; \theta, \beta) + ( A(s, a; \theta, \alpha) − \frac{1} {|A|} \sum_ {a'} A(s, a'; \theta, \alpha) )
|
||||
$$
|
||||
|
||||
## **四、** 实验
|
||||
|
||||
### 4.1 策略评估
|
||||
|
||||
为了评估学习到的 $Q$ 值，论文选择了一个简单的环境，其中可以为所有 $(s, a) ∈ S × A$ 分别计算准确的 $Q_\pi(s,a)$值。
|
||||
|
||||
这个环境，称之为走廊，由三个相连的走廊组成。走廊环境示意图如（a）所示，智能体从环境的左下角开始，必须移动到右上角才能获得最大的奖励。共有 5 种动作可用：上、下、左、右和无操作。两个垂直部分都有 10 个状态，而水平部分有 50 个状态。
|
||||
|
||||
论文在走廊环境的三种变体上分别使用 5、10 和 20 个动作将单流 Q 架构与Dueling Network架构进行了比较（10 和 20 动作变体是通过在原始环境中添加无操作而形成的）。
|
||||
|
||||
单流架构是一个三层 MLP，每个隐藏层有 50 个单元。Dueling Network架构也由三层组成。然而，在 50 个单元的第一个隐藏层之后，网络分支成两个流，每个流都是具有 25 个隐藏单元的两层 MLP。
|
||||
|
||||
|
||||
|
||||
结果表明，通过 5 个动作，两种架构以大致相同的速度收敛。然而，当我们增加动作数量时，Dueling Network架构比传统的 Q 网络表现更好。在Dueling Network中，流 $V (s; θ, β)$ 学习到一个通用值，该值在状态 $s$ 处的许多相似动作之间共享，从而导致更快的收敛。
|
||||
|
||||
### 4.2 General Atari Game-Playing
|
||||
|
||||
论文在由 57 个 Atari 游戏组成的 Arcade Learning Environment上对提出的方法进行了综合评估。
|
||||
|
||||
论文的网络架构具有与 DQN 相同的低级卷积结构。有 3 个卷积层，后面是 2 个全连接层。第一个卷积层有 32 个步长为 4 的 8×8 滤波器，第二个是 64 个步长为 2 的 4×4 滤波器，第三个也是最后一个卷积层由 64 个步长为 1 的 3×3 滤波器组成。由于A和V流都将梯度传播到反向传播中的最后一个卷积层，论文将进入最后一个卷积层的组合梯度重新缩放 1/√2。这种简单的启发式方法温和地增加了稳定性。此外，我们对梯度进行裁剪，使其范数小于或等于 10。
|
||||
|
||||
**评估函数：**
|
||||
|
||||
$$
|
||||
30 no-op=\frac{Score_{Agent} − Score_{Baseline}} {max\{Score_{Human}, Score_{Baseline}\} − Score_{Random}}
|
||||
$$
|
||||
|
||||
**结果：**
|
||||
|
||||
|
||||
|
||||
Single Clip 的性能优于 Single。我们验证了这种增益主要是由梯度裁剪带来的。出于这个原因，我们在所有新方法中都加入了梯度裁剪。Duel Clip 在 75.4% 的游戏中（57 场中有 43 场）的表现优于 Single Clip。与单一基线相比，它在 80.7%（57 场比赛中的 46 场）的比赛中也获得了更高的分数。在所有有 18 个动作的游戏中，Duel Clip 有 86.6% 的几率更好（30 个中有 26 个）。这与上一节的研究结果一致。总体而言，Duel智能体 (Duel Clip) 在 57 场比赛中的 42 场比赛中达到了人类水平的表现。
|
||||
|
||||
## 五、贡献
|
||||
|
||||
1. 能够使Q网络更好地收敛。因为针对动作价值Q ，传统的DQN算法直接进行Q值估计，而Dueling DQN则是将其拆分为两项：V和A，即状态价值函数V和优势函数 A，这样的好处就是能够在Q值相近的时候，通过拆解出来的A找到那个最优的动作。
|
||||
|
||||
2. 鲁棒性更好。在给定状态的 Q 值之间的差异通常非常小的情况下，这种尺度差异可能导致更新中的少量噪声可能导致动作的重新排序，从而使策略突然切换。但是因为有具有优势函数A，所以Dueling Network架构对这种效果具有鲁棒性。
|
||||
|
||||
## 六、个人介绍
|
||||
|
||||
程岳，研究生，重庆邮电大学，目前研究方向为模糊时间序列分析、多源异构数据融合，大数据分析与智能决策重庆市重点实验室。
|
||||
Binary file not shown.
Binary file not shown.
Binary file not shown.
Binary file not shown.
BIN
papers/DQN/PDF/Prioritized Experience Replay.pdf
Normal file
BIN
papers/DQN/PDF/Prioritized Experience Replay.pdf
Normal file
Binary file not shown.
Binary file not shown.
64
papers/DQN/Playing Atari with Deep Reinforcement Learning.md
Normal file
64
papers/DQN/Playing Atari with Deep Reinforcement Learning.md
Normal file
@@ -0,0 +1,64 @@
|
||||
## Playing Atari with Deep Reinforcement Learning
|
||||
|
||||
作者： Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Alex Graves, Ioannis Antonoglou, Daan Wierstra, Martin Riedmiller
|
||||
|
||||
单位：Deepmind
|
||||
|
||||
论文链接：https://arxiv.org/abs/1312.5602
|
||||
|
||||
**亮点：作者提出了用深度学习模型来拟合价值函数，结合Q-Learning进行训练的深度强化学习算法DQN，并且在Atari 2600上进行了验证。**
|
||||
|
||||
### **Motivation (Why):**
|
||||
|
||||
传统RL依赖手工特征和线性的价值函数，性能受限。DL的技术进步，可以在原始数据中提取高维信息，不需要再手工提取特征。如果把DL和RL结合起来，RL算法性能可以显著提升，但是这有以下两个问题要克服：
|
||||
|
||||
1. DL算法需要大量有标签的数据，而RL算法的训练只能返回一个标量的奖励，并且是稀疏、充满噪声和延迟的。
|
||||
2. DL需要数据是独立同分布的，而RL算法的数据既不是独立的，分布也不是固定的。RL算法中的状态之间往往是高度相关的，而且RL的数据分布也会随着算法开始学习新的行为而改变。
|
||||
|
||||
### **Main Idea (What):**
|
||||
|
||||
作者通过使用一个CNN网络和Q-Learning算法结合的DQN算法来解决上述问题。具体来说，动机中的DL算法需要大量有标签数据的问题是由Q-Learning训练中的Fixed Q-target思路解决的，而RL算法中数据不是独立同分布的问题是通过经验回放来缓解（alleviate）的。
|
||||
|
||||
### **Main Contribution (How):**
|
||||
|
||||
与之前TD-Gammon直接在On-policy的策略中学习不同，DQN采取了Off-policy的形式，将采样数据存在一个固定大小的名为经验回放池的集合中，训练中将集合划分成多个Mini-batch，采用SGD优化器更新权重。对于在Q-learning中使用经验回放策略来缓解非独立同分布的问题，本文提出的算法如下图所示：
|
||||
|
||||
|
||||
|
||||
以上是DQN完整的算法，算法根据 $\epsilon$ -贪婪策略在状态 $s_t$ 选择并执行一个行动 $a_t$， 观测系统给出的奖励 $r_t$ 以及采取动作后的游戏画面 $x_{t+1}$, 由于使用任意长度的历史作为神经网络的输入是很困难的，因此作者通过序列转换函数 $\phi()$，将序列 $s_{t+1} = s_t,a_t,x_t+1$ 转化成 状态向量 $s_{t+1}$, 使Q函数可以在固定长度的历史上工作。此外，作者利用一种被称为经验重放的技术， 将算法在不同回合中各时间步长采集的经验数据 $e_t = (s_t, a_t, r_t, s_{t+1})$ 汇总存放在一个经验重放存储器 $D=e_1，...，e_N$ 中。在算法内循环中需要对模型进行更新的时候，我们从存储样本的经验重放存储器中随机抽取样本，对模型参数进行更新。
|
||||
|
||||
**本文提出方法的优点：**
|
||||
|
||||
1. Q函数的输入是状态，不是状态-动作对，可以有效减少模型计算量。前者只需要一次计算，将不同动作作为输出层的神经元，选取值最大的那个动作，后者则需要对每个动作都进行一次计算。
|
||||
2. 权重更新是SGD的形式，不是OGD的。可以提高样本利用率，并且对不同状态下不同行为对应Q函数的分布进行平均和平滑处理，避免算法不收敛。
|
||||
|
||||
**待改进的地方：**
|
||||
|
||||
经验回放部分只储存最近的经验，并且取样的时候是随机取样的，并不区分比较重要的样本，还因为内存问题不停地覆盖先前的经验。可以用更复杂的取样策略，来区分出哪些样本更重要并加以利用。
|
||||
|
||||
**结果：**
|
||||
|
||||
|
||||
|
||||
DQN在7个Atari 2600游戏上的得分有6个超过了最好方法，有3个游戏超过了人类专家，但在Q*bert、Seaquest、Space Invaders等游戏上与人类相差甚远，作者评价它们更具挑战性，需要要求网络找到可以延伸到更长时间尺度的策略。
|
||||
|
||||
|
||||
|
||||
**个人思考**
|
||||
|
||||
1. 作者在这7个游戏上用的是同一种网络和算法以及同样的超参数。
|
||||
2. 可能是为了突出这是第一篇DL和RL的文章，作者在文中不停地强调DQN用的就是游戏的原始图像，没有做任何人工提取特征的工作，并且除迫不得已的原因外（游戏设置问题）在训练和测试都没有对超参数进行改动。
|
||||
3. 作者前文中也提到了非线性价值函数往往缺少收敛性的保证，这也导致了之前的大量研究都是用收敛性的更好的线性价值函数。但在DQN的实验中仍没有做收敛性的理论分析，只是说在大量的实验中我们没有遇到这个问题。
|
||||
|
||||
|
||||
|
||||
### 个人简介
|
||||
|
||||
吴文昊，西安交通大学硕士在读
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
534
papers/DQN/Prioritized Experience Replay.md
Normal file
534
papers/DQN/Prioritized Experience Replay.md
Normal file
@@ -0,0 +1,534 @@
|
||||
# JoyRL论文阅读《Prioritized Experience Replay》 + Python代码
|
||||
作者：Tom Schaul, John Quan, Ioannis Antonoglou and David Silver
|
||||
|
||||
实验室：Google DeepMind
|
||||
|
||||
邮箱：{schaul,johnquan,ioannisa,davidsilver}@google.com
|
||||
|
||||
论文地址：[https://arxiv.org/abs/1511.05952](https://arxiv.org/abs/1511.05952) Published as a conference paper at ICLR 2016
|
||||
|
||||
- **<u>*标题有问题*</u>**
|
||||
|
||||
|
||||
## 一、提出背景
|
||||
**深度强化学习算法**，结合了深度学习强大的环境感知能力和强化学习的决策能力，近年来被广泛应用于游戏、无人自主导航、多智能体协作以及推荐系统等各类人工智能新兴领域。强化学习作为机器学习的一个重要分支，其本质是智能体以“**试错**”的方式在与环境中学习策略，与常见的监督学习和非监督学习不同，强化学习强调智能体与环境之间的交互，在交互过程中通过不断学习来改变策略得到最大回报，以得到最优策略。
|
||||
|
||||
强化学习由于其算法特性，并没有现成的数据集，而仅靠单步获得的数据对未知的复杂环境信息进行感知决策并不高效可靠。DQN算法结合神经网络的同时，结合了**经验回放机制**，针对Q-learning的局限性，打消了采样数据相关性，使得数据分布变得更稳定。
|
||||
|
||||
但随着DQN算法的应用，研究人员发现，基于经验回放机制的DQN算法，仅采用**均匀采样**和**批次更新**，导致部分数量少但价值高的经验没有被高效的利用。针对上述情况，Deep Mind团队提出了**Prioritized Experience Replay（优先经验回放）机制**，本文将对该论文展开详细介绍。
|
||||
|
||||
## 二、摘要和结论
|
||||
### 1 摘要
|
||||
经验重放（Experience replay）使在线强化学习（Online reinforcement learning）智能体可以记住和重用过去的经验。先前的经验重放是从存储器中统一采样，只是以与最初经验的相同频率进行重采样，而不管其重要性如何。该论文开发了一个优先考虑经验的框架，以便更频繁地重播重要的数据，从而更有效地学习。文章中将优先经验回放机制与DQN网络结合，在49场比赛中有41场具有统一重播的DQN表现优于DQN。
|
||||
|
||||
### 2 结论
|
||||
文章为经验回放机制及其几个变体，设计了可以扩展到大型重放内存的实现，发现优先级重放可以将学习速度提高2倍，并在Atari Baseline上带来了最新的性能。
|
||||
|
||||
## 三、基本理论
|
||||
### 1 经验回放（Experience Replay）：
|
||||
- 创建一个经验池（Experience Replay Buffer），每一次Agent选择一个动作与环境交互就会储存一组数据$e_t = (s_t, a_t, r_t, s_{t+1})$到经验池中。
|
||||
|
||||
- 维护这个经验池（队列），当储存的数据组数到达一定的阈值，数据到就会从队列中被提取出来。
|
||||
|
||||
- 采用均匀采样的方式进行数据提取。
|
||||
|
||||
上述方法解决了经验数据的相关性（Correlated data）和非平稳分布（Non-stationary distribution）问题。它的做法是从以往的状态转移（经验）中**均匀采样**进行训练。优点是数据利用率高，一个样本被多次使用，且连续样本的相关性会使参数更新的方差（Variance）比较大，以此减少这种相关性。
|
||||
|
||||
然而，采用均匀采样方式存在的问题，作者举了例子如图所示：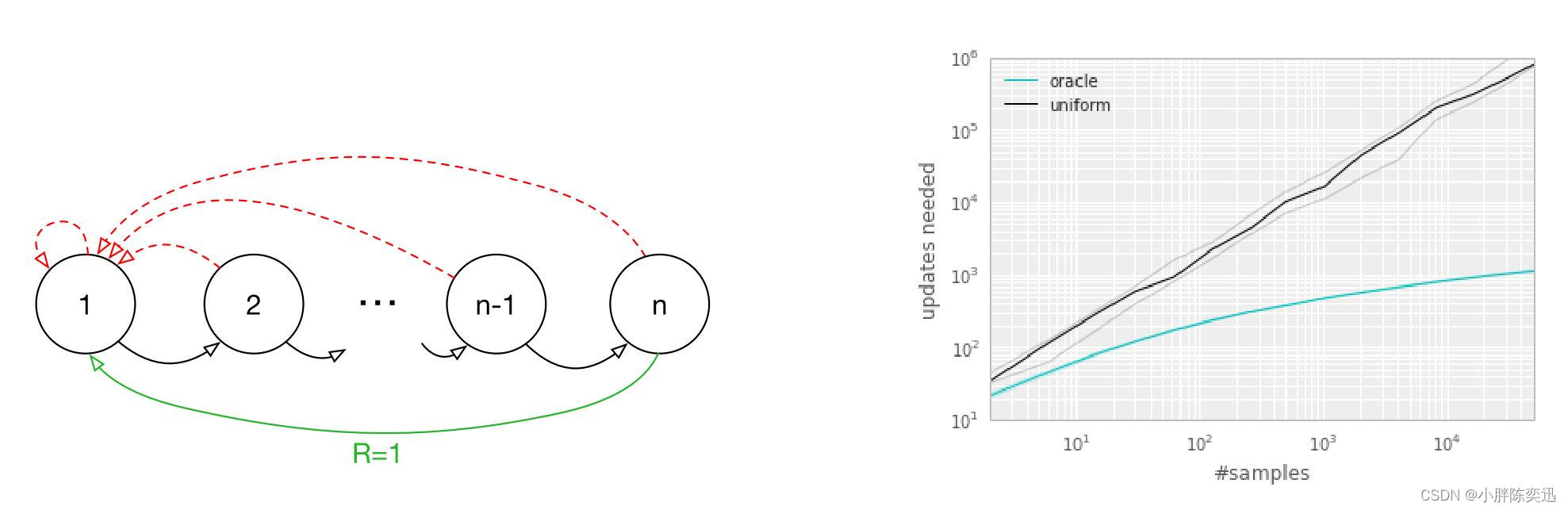
|
||||
左图表示一个（稀疏奖励）环境有初始状态为1，有n个状态，两个可选动作，仅当选择绿色线条动作的时候可以得到 reward=1 的奖励；右图为实验结果，黑色曲线代表均匀采样的结果，蓝色曲线为研究人员提出的一个名为“oracle”的最优次序，即每次采样的transition均采用“最好”的结果，实验结果可看出每次采用最优次序的方法在稀疏奖励（Reward sparse）环境能够明显优于均匀采样。
|
||||
|
||||
那么如何在实际应用当中找到这个“最优”次序，即如何在采样前提前设计好一个次序，使得每次采样的数据都尽可能让agent高效学习呢？
|
||||
### 2 优先经验回放（Prioritized Experience Replay，PER）
|
||||
针对经验回放机制存在的问题，DeepMind团队提出了两方面的思考：要存储哪些经验（**which experiences to store**），以及要重放哪些经验（**which experiences to replay，and how to do so**）。论文中仅针对后者，即怎么样选取要采样的数据以及实验的方法做了详尽的说明和研究。
|
||||
|
||||
PER机制将TD-error（时序误差）作为衡量标准评估被采样数据的优先级。TD-error指在时序差分中**当前Q值**和它**目标Q值**的差值,误差越大即表示该数据对网络参数的更新越有帮助。贪婪（选取最大值）的采样TD-error大的数据训练，理论上会加速收敛，但随之而来也会面临以下问题：
|
||||
|
||||
- TD-error可看做对参数更新的信息增益，信息增益较大仅表示对于当前的价值网络参数而言增益较大，但却不能代表对于后续的价值网络没有较大的增益。若只贪婪的考虑信息增益来采样，当前TD-error较小的数据优先级会越来越低，后面会越来越难采样到该组数据。
|
||||
|
||||
- 贪婪的选择使得神经网络总是更新某一部分样本，即“经验的一个子集”，很可能导致陷入局部最优，亦或是过估计的发生。
|
||||
|
||||
针对上述PER存在的问题，作者在文中提出了一种随机抽样的方法，该方法介于纯贪婪和均匀随机之间，确保transition基于优先级的被采样概率是单调的，同时即使对于最低优先级的transition也保证非零的概率，随机抽样的方法将在***<u>1.3展开</u>***介绍。
|
||||
|
||||
## 四、相关改进工作
|
||||
### 1 随机优先级（Stochastic Prioritization）
|
||||
论文将采样transition $i$的概率定义为：
|
||||
$$P(i)=\frac{p_i^\alpha}{\sum_k p_k^\alpha}$$
|
||||
其中$p_i>0$表示transition $i$的优先级。指数$α$表示决定使用多少优先级，可看做一个trade-off因子，用来权衡uniform和greedy的程度，当$α=0$时表示均匀采样，$α=1$是表示贪婪（选取最大值）采样。
|
||||
|
||||
在DQN中：$\delta=y -Q(s, a)$, $\delta$表示TD-error，即每一步当前Q值与目标值$y$之间的差值，在更新过程中也是为了让$\delta^2$的期望尽可能的小。
|
||||
|
||||
文中将随机优先经验回放划分为以下两个类型：
|
||||
|
||||
a）直接的，基于比例的：**Proportional Prioritization**
|
||||
|
||||
b）间接的，基于排名的：**Rank-based Prioritization**
|
||||
|
||||
- **a）Proportional Prioritization**中，根据 $|\delta|$决定采样概率：
|
||||
|
||||
$$p_i=\left|\delta_i\right|+\epsilon$$
|
||||
其中 $\delta$表示TD-eroor，$\epsilon$是一个大于0的常数，为了保证无论TD-error取值如何，采样概率$p_i$仍大于0，即仍有概率会被采样到。
|
||||
- **b）Rank-based Prioritization**中，根据 $|\delta|$ 的 **排名（Rank）** 来决定采样概率：
|
||||
|
||||
$$p_i=\frac{1}{\operatorname{rank}(i)}$$
|
||||
|
||||
作者在文中对两种方法进行了比较：
|
||||
|
||||
**a）从理论层次分析：**
|
||||
**proportional prioritization**优势在于可以直接获得 $|\delta|$ 的信息，也就是它的信息增益多一些；而**rank-based prioritization**则没有 $|\delta|$ 的信息，但其对异常点不敏感，因为异常点的TD-error过大或过小对rank值没有太大影响，也正因为此，**rank-based prioritization**具有更好的鲁棒性。
|
||||
|
||||
**b）从实验层次分析：**
|
||||
结果如下图所示，可以看出这两种方法的表现大致相同。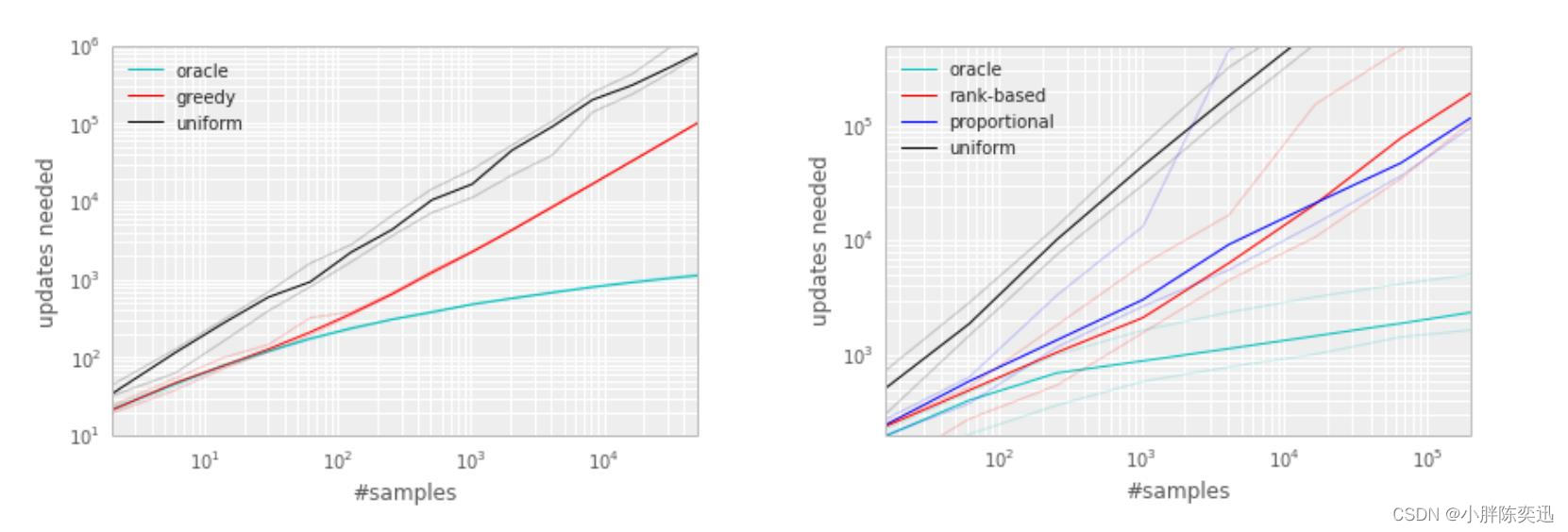
|
||||
### 2 SumTree
|
||||
Proportional Prioritization的实现较为复杂，可借助SumTree数据结构完成。SumTree是一种树形结构，每片树叶存储每个样本的优先级P，每个树枝节点只有两个分叉，节点的值是两个分叉的和，所以SumTree的顶端就是所有p的和。结构如下图([引自jaromiru.com](https://jaromiru.com/2016/11/07/lets-make-a-dqn-double-learning-and-prioritized-experience-replay/))所示, 顶层的节点是全部p的和。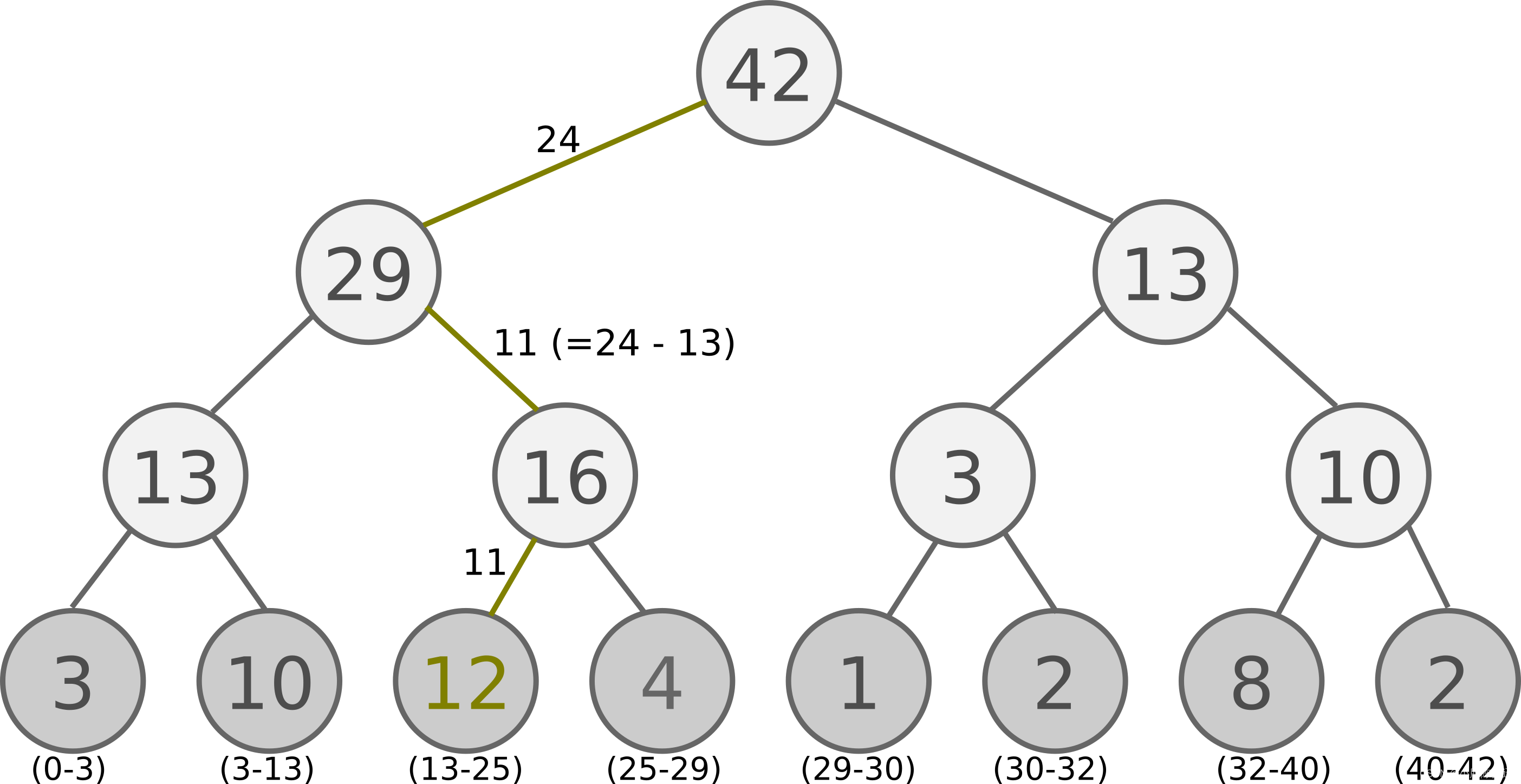
|
||||
抽样时, 我们会将 p 的总和除以 batch size, 分成 batch size 多个区间，即$n={ sum(p) }/{batchsize}$.。如果将所有节点的优先级加起来是42, 我们如果抽6个样本, 这时的区间拥有的 priority 可能是这样:[0-7], [7-14], [14-21], [21-28], [28-35], [35-42]
|
||||
|
||||
然后在每个区间里随机选取一个数. 比如在第区间 [21-28] 里选到了24, 就按照这个 24 从最顶上的42开始向下搜索. 首先看到最顶上 42 下面有两个 child nodes, 拿着手中的24对比左边的 child 29, 如果左边的 child 比自己手中的值大, 那我们就走左边这条路, 接着再对比 29 下面的左边那个点 13, 这时, 手中的 24 比 13 大, 那我们就走右边的路, 并且将手中的值根据 13 修改一下, 变成 24-13 = 11. 接着拿着 11 和 13 左下角的 12 比, 结果 12 比 11 大, 那我们就选 12 当做这次选到的 priority, 并且也选择 12 对应的数据。
|
||||
|
||||
以上面的树结构为例，根节点是42，如果要采样一个样本，我们可以在[0,42]之间做均匀采样，采样到哪个区间，就是哪个样本。比如我们采样到了26， 在（25-29）这个区间，那么就是第四个叶子节点被采样到。而注意到第三个叶子节点优先级最高，是12，它的区间13-25也是最长的，所以它会比其他节点更容易被采样到。
|
||||
|
||||
如果要采样两个样本，我们可以在[0,21],[21,42]两个区间做均匀采样，方法和上面采样一个样本类似。
|
||||
### 3 消除偏差（Annealing the Bias）
|
||||
使用优先经验回放还存在一个问题是改变了状态的分布，DQN中引入经验池是为了解决数据相关性，使数据（尽量）独立同分布。但是使用优先经验回放又改变了状态的分布，这样势必会引入偏差bias，对此，文中使用重要性采样结合退火因子来消除引入的偏差。
|
||||
|
||||
在DQN中，梯度的计算如下所示：
|
||||
$$
|
||||
\nabla_{\theta_i} L\left(\theta_i\right)=\mathbb{E}_{s, a, r, s^{\prime}}\left[\left(r+\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime} ; \theta_i\right)-Q\left(s, a ; \theta_i\right)\right) \nabla_{\theta_i} Q\left(s, a ; \theta_i\right)\right]（1）
|
||||
$$
|
||||
在随机梯度下降（SGD）中可表示为：
|
||||
$$
|
||||
\nabla_\theta L(\theta)=\delta \nabla_\theta Q(s, a)
|
||||
$$
|
||||
而重要性采样，就是给这个梯度加上一个权重$w$
|
||||
$$
|
||||
\nabla_\theta L(\theta)=w \delta \nabla_\theta Q(s, a)
|
||||
$$
|
||||
重要性采样权重$w_i$在文中定义为：
|
||||
$$
|
||||
w_i=\left(\frac{1}{N} \cdot \frac{1}{P(i)}\right)^\beta
|
||||
$$
|
||||
$N$ 表示Buffer里的样本数，而 $\beta$ 是一个超参数，用来决定多大程度想抵消 Prioritized Experience Replay对收敛结果的影响。如果 $\beta=0$，表示完全不使用重要性采样 ；$\beta=1$时表示完全抵消掉影响，由于 $(s, a)$ 不再是均匀分布随机选出来的了，而是以 $P(i)$ 的概率选出来，因此，如果 $\beta=1$ ， 那么 $w$ 和 $P(i)$ 就正好抵消了，于是Prioritized Experience Replay的作用也就被抵消了，即$\beta=1$等同于DQN中的 Experience Replay。
|
||||
|
||||
为了稳定性，我们需要对权重 $w$ 归一化，但是不用真正意义上的归一化，只要除上 $\max _i w_i$ 即可，即：
|
||||
|
||||
$$
|
||||
w_j=(N * P(j))^{-\beta} / \max _i\left(w_i\right)
|
||||
$$
|
||||
|
||||
归一化后的 $w_i$ 在编写代码时可推导转化为：
|
||||
|
||||
$$
|
||||
w_j=\frac{(N * P(j))^{-\beta}}{\max _i\left(w_i\right)}=\frac{(N * P(j))^{-\beta}}{\max _i\left((N * P(i))^{-\beta}\right)}=\frac{(P(j))^{-\beta}}{\max _i\left((P(i))^{-\beta}\right)}=\left(\frac{P_j}{\min _i P(i)}\right)^{-\beta}
|
||||
$$
|
||||
|
||||
## 五、PER代码
|
||||
### 1 Prioritized Replay DQN 算法流程
|
||||
**算法输入**：迭代轮数 $T$ ，状态特征维度 $n$ ，动作集 $A$ ，步长 $\alpha$ ，采样权重系数 $\beta$ ，衰减因子 $\gamma$ ，探索率 $\epsilon$ ，当前 $Q$ 网络 $Q$ ，目标 $\mathrm{Q}$ 网络 $Q^{\prime}$ ，批量梯度下降的样本数 $m$ ，目标 $\mathrm{Q}$ 网络参数更新频率 $C$ ，SumTree的叶子节点数 $S$ 。
|
||||
|
||||
**输出**: Q网络参数。
|
||||
|
||||
1. 随机初始化所有的状态和动作对应的价值 $Q$. 随机初始化当前 $\mathrm{Q}$ 网络的所有参数 $w$, 初始化目标Q网络 $Q^{\prime}$ 的参数 $w^{\prime}=w$ 。初始化经验回放SumTree 的默认数据结构，所有SumTree的 $S$ 个叶子节点的优先级 $p_j$ 为 1 。
|
||||
|
||||
2. for i from 1 to $T$ ，进行迭代。
|
||||
|
||||
a) 初始化S为当前状态序列的第一个状态，得到其特征向量 $\phi(S)$
|
||||
|
||||
b) 在 $\mathrm{Q}$ 网络中使用 $\phi(S)$ 作为输入，得到 $\mathrm{Q}$ 网络的所有动作对应的 $\mathrm{Q}$ 值输出。用 $\epsilon$ 一贪婪法在当前 $\mathrm{Q}$ 值输出中选择对应的动作 $A$
|
||||
|
||||
c) 在状态 $S$ 执行当前动作 $A$, 得到新状态 $S^{\prime}$ 对应的特征向量 $\phi\left(S^{\prime}\right)$ 和奖励 $R$, 是否终止状态is_end
|
||||
|
||||
d) 将 $\left\{\phi(S), A, R, \phi\left(S^{\prime}\right), i s_{-} e n d\right\}$ 这个五元组存入SumTree
|
||||
|
||||
e) $S=S^{\prime}$
|
||||
|
||||
f) 从SumTree中采样 $m$ 个样本 $\left\{\phi\left(S_j\right), A_j, R_j, \phi\left(S_j^{\prime}\right), i s_{-} e n d_j\right\}, j=1,2 .,,, m$，每个样本被采样的概率基于 $P(j)=\frac{p_j}{\sum_i\left(p_i\right)}$ ，损失函数权重 $w_j=(N * P(j))^{-\beta} / \max _i\left(w_i\right)$ ，计算当前目标Q值 $y_j$ :
|
||||
|
||||
$$
|
||||
y_j= \begin{cases}R_j & \text { is end }_j \text { is true } \\ R_j+\gamma Q^{\prime}\left(\phi\left(S_j^{\prime}\right), \arg \max _{a^{\prime}} Q\left(\phi\left(S_j^{\prime}\right), a, w\right), w^{\prime}\right) & \text { is end }_j \text { is false }\end{cases}
|
||||
$$
|
||||
|
||||
g)使用均方差损失函数 $\frac{1}{m} \sum_{j=1}^m w_j\left(y_j-Q\left(\phi\left(S_j\right), A_j, w\right)\right)^2$ ，通过神经网络的梯度反向传播来更新Q网络的所有参数 $w$
|
||||
|
||||
h) 重新计算所有样本的TD误差 $\delta_j=y_j-Q\left(\phi\left(S_j\right), A_j, w\right)$，更新SumTree中所有节点的优先级 $p_j=\left|\delta_j\right|$
|
||||
|
||||
i) 如果 $\mathrm{i} \% \mathrm{C}=1$, 则更新目标 $\mathrm{Q}$ 网络参数 $w^{\prime}=w$
|
||||
|
||||
j) 如果 $S^{\prime}$ 是终止状态，当前轮迭代完毕，否则转到步骤b)
|
||||
|
||||
|
||||
### 2 相关代码
|
||||
该部分代码可直接在程序里调用，其中ReplayBuffer（）这个类是传统的的经验回放；PrioritizedReplayBuffer(ReplayBuffer)这个类是优先经验回放。
|
||||
|
||||
```python
|
||||
import numpy as np
|
||||
import random
|
||||
|
||||
from segment_tree import SumSegmentTree, MinSegmentTree
|
||||
|
||||
|
||||
class ReplayBuffer(object):
|
||||
def __init__(self, size):
|
||||
"""Create Replay buffer.
|
||||
|
||||
Parameters
|
||||
----------
|
||||
size: int
|
||||
Max number of transitions to store in the buffer. When the buffer
|
||||
overflows the old memories are dropped.
|
||||
"""
|
||||
self._storage = []
|
||||
self._maxsize = size
|
||||
self._next_idx = 0
|
||||
|
||||
def __len__(self):
|
||||
return len(self._storage)
|
||||
|
||||
def add(self, obs_t, action, reward, obs_tp1, done):
|
||||
data = (obs_t, action, reward, obs_tp1, done)
|
||||
|
||||
if self._next_idx >= len(self._storage):
|
||||
self._storage.append(data)
|
||||
else:
|
||||
self._storage[self._next_idx] = data
|
||||
self._next_idx = (self._next_idx + 1) % self._maxsize
|
||||
|
||||
def _encode_sample(self, idxes):
|
||||
obses_t, actions, rewards, obses_tp1, dones = [], [], [], [], []
|
||||
for i in idxes:
|
||||
data = self._storage[i]
|
||||
obs_t, action, reward, obs_tp1, done = data
|
||||
obses_t.append(np.array(obs_t, copy=False))
|
||||
actions.append(np.array(action, copy=False))
|
||||
rewards.append(reward)
|
||||
obses_tp1.append(np.array(obs_tp1, copy=False))
|
||||
dones.append(done)
|
||||
return np.array(obses_t), np.array(actions), np.array(rewards), np.array(obses_tp1), np.array(dones)
|
||||
|
||||
def sample(self, batch_size):
|
||||
"""Sample a batch of experiences.
|
||||
|
||||
Parameters
|
||||
----------
|
||||
batch_size: int
|
||||
How many transitions to sample.
|
||||
|
||||
Returns
|
||||
-------
|
||||
obs_batch: np.array
|
||||
batch of observations
|
||||
act_batch: np.array
|
||||
batch of actions executed given obs_batch
|
||||
rew_batch: np.array
|
||||
rewards received as results of executing act_batch
|
||||
next_obs_batch: np.array
|
||||
next set of observations seen after executing act_batch
|
||||
done_mask: np.array
|
||||
done_mask[i] = 1 if executing act_batch[i] resulted in
|
||||
the end of an episode and 0 otherwise.
|
||||
"""
|
||||
idxes = [random.randint(0, len(self._storage) - 1) for _ in range(batch_size)]
|
||||
return self._encode_sample(idxes)
|
||||
|
||||
|
||||
class PrioritizedReplayBuffer(ReplayBuffer):
|
||||
def __init__(self, size, alpha):
|
||||
"""Create Prioritized Replay buffer.
|
||||
|
||||
Parameters
|
||||
----------
|
||||
size: int
|
||||
Max number of transitions to store in the buffer. When the buffer
|
||||
overflows the old memories are dropped.
|
||||
alpha: float
|
||||
how much prioritization is used
|
||||
(0 - no prioritization, 1 - full prioritization)
|
||||
|
||||
See Also
|
||||
--------
|
||||
ReplayBuffer.__init__
|
||||
"""
|
||||
super(PrioritizedReplayBuffer, self).__init__(size)
|
||||
assert alpha >= 0
|
||||
self._alpha = alpha
|
||||
|
||||
it_capacity = 1
|
||||
while it_capacity < size:
|
||||
it_capacity *= 2
|
||||
|
||||
self._it_sum = SumSegmentTree(it_capacity)
|
||||
self._it_min = MinSegmentTree(it_capacity)
|
||||
self._max_priority = 1.0
|
||||
|
||||
def add(self, *args, **kwargs):
|
||||
"""See ReplayBuffer.store_effect"""
|
||||
idx = self._next_idx
|
||||
super().add(*args, **kwargs)
|
||||
self._it_sum[idx] = self._max_priority ** self._alpha
|
||||
self._it_min[idx] = self._max_priority ** self._alpha
|
||||
|
||||
def _sample_proportional(self, batch_size):
|
||||
res = []
|
||||
p_total = self._it_sum.sum(0, len(self._storage) - 1)
|
||||
every_range_len = p_total / batch_size
|
||||
for i in range(batch_size):
|
||||
mass = random.random() * every_range_len + i * every_range_len
|
||||
idx = self._it_sum.find_prefixsum_idx(mass)
|
||||
res.append(idx)
|
||||
return res
|
||||
|
||||
def sample(self, batch_size, beta):
|
||||
"""Sample a batch of experiences.
|
||||
|
||||
compared to ReplayBuffer.sample
|
||||
it also returns importance weights and idxes
|
||||
of sampled experiences.
|
||||
|
||||
|
||||
Parameters
|
||||
----------
|
||||
batch_size: int
|
||||
How many transitions to sample.
|
||||
beta: float
|
||||
To what degree to use importance weights
|
||||
(0 - no corrections, 1 - full correction)
|
||||
|
||||
Returns
|
||||
-------
|
||||
obs_batch: np.array
|
||||
batch of observations
|
||||
act_batch: np.array
|
||||
batch of actions executed given obs_batch
|
||||
rew_batch: np.array
|
||||
rewards received as results of executing act_batch
|
||||
next_obs_batch: np.array
|
||||
next set of observations seen after executing act_batch
|
||||
done_mask: np.array
|
||||
done_mask[i] = 1 if executing act_batch[i] resulted in
|
||||
the end of an episode and 0 otherwise.
|
||||
weights: np.array
|
||||
Array of shape (batch_size,) and dtype np.float32
|
||||
denoting importance weight of each sampled transition
|
||||
idxes: np.array
|
||||
Array of shape (batch_size,) and dtype np.int32
|
||||
idexes in buffer of sampled experiences
|
||||
"""
|
||||
assert beta > 0
|
||||
|
||||
idxes = self._sample_proportional(batch_size)
|
||||
|
||||
weights = []
|
||||
p_min = self._it_min.min() / self._it_sum.sum()
|
||||
max_weight = (p_min * len(self._storage)) ** (-beta)
|
||||
|
||||
for idx in idxes:
|
||||
p_sample = self._it_sum[idx] / self._it_sum.sum()
|
||||
weight = (p_sample * len(self._storage)) ** (-beta)
|
||||
weights.append(weight / max_weight)
|
||||
weights = np.array(weights)
|
||||
encoded_sample = self._encode_sample(idxes)
|
||||
return tuple(list(encoded_sample) + [weights, idxes])
|
||||
|
||||
def update_priorities(self, idxes, priorities):
|
||||
"""Update priorities of sampled transitions.
|
||||
|
||||
sets priority of transition at index idxes[i] in buffer
|
||||
to priorities[i].
|
||||
|
||||
Parameters
|
||||
----------
|
||||
idxes: [int]
|
||||
List of idxes of sampled transitions
|
||||
priorities: [float]
|
||||
List of updated priorities corresponding to
|
||||
transitions at the sampled idxes denoted by
|
||||
variable `idxes`.
|
||||
"""
|
||||
assert len(idxes) == len(priorities)
|
||||
for idx, priority in zip(idxes, priorities):
|
||||
assert priority > 0
|
||||
assert 0 <= idx < len(self._storage)
|
||||
self._it_sum[idx] = priority ** self._alpha
|
||||
self._it_min[idx] = priority ** self._alpha
|
||||
|
||||
self._max_priority = max(self._max_priority, priority)
|
||||
|
||||
```
|
||||
以上代码调用的数据结构SumTree，代码如下：
|
||||
|
||||
```python
|
||||
import operator
|
||||
|
||||
|
||||
class SegmentTree(object):
|
||||
def __init__(self, capacity, operation, neutral_element):
|
||||
"""Build a Segment Tree data structure.
|
||||
|
||||
https://en.wikipedia.org/wiki/Segment_tree
|
||||
|
||||
Can be used as regular array, but with two
|
||||
important differences:
|
||||
|
||||
a) setting item's value is slightly slower.
|
||||
It is O(lg capacity) instead of O(1).
|
||||
b) user has access to an efficient ( O(log segment size) )
|
||||
`reduce` operation which reduces `operation` over
|
||||
a contiguous subsequence of items in the array.
|
||||
|
||||
Paramters
|
||||
---------
|
||||
capacity: int
|
||||
Total size of the array - must be a power of two.
|
||||
operation: lambda obj, obj -> obj
|
||||
and operation for combining elements (eg. sum, max)
|
||||
must form a mathematical group together with the set of
|
||||
possible values for array elements (i.e. be associative)
|
||||
neutral_element: obj
|
||||
neutral element for the operation above. eg. float('-inf')
|
||||
for max and 0 for sum.
|
||||
"""
|
||||
assert capacity > 0 and capacity & (capacity - 1) == 0, "capacity must be positive and a power of 2."
|
||||
self._capacity = capacity
|
||||
self._value = [neutral_element for _ in range(2 * capacity)]
|
||||
self._operation = operation
|
||||
|
||||
def _reduce_helper(self, start, end, node, node_start, node_end):
|
||||
if start == node_start and end == node_end:
|
||||
return self._value[node]
|
||||
mid = (node_start + node_end) // 2
|
||||
if end <= mid:
|
||||
return self._reduce_helper(start, end, 2 * node, node_start, mid)
|
||||
else:
|
||||
if mid + 1 <= start:
|
||||
return self._reduce_helper(start, end, 2 * node + 1, mid + 1, node_end)
|
||||
else:
|
||||
return self._operation(
|
||||
self._reduce_helper(start, mid, 2 * node, node_start, mid),
|
||||
self._reduce_helper(mid + 1, end, 2 * node + 1, mid + 1, node_end)
|
||||
)
|
||||
|
||||
def reduce(self, start=0, end=None):
|
||||
"""Returns result of applying `self.operation`
|
||||
to a contiguous subsequence of the array.
|
||||
|
||||
self.operation(arr[start], operation(arr[start+1], operation(... arr[end])))
|
||||
|
||||
Parameters
|
||||
----------
|
||||
start: int
|
||||
beginning of the subsequence
|
||||
end: int
|
||||
end of the subsequences
|
||||
|
||||
Returns
|
||||
-------
|
||||
reduced: obj
|
||||
result of reducing self.operation over the specified range of array elements.
|
||||
"""
|
||||
if end is None:
|
||||
end = self._capacity
|
||||
if end < 0:
|
||||
end += self._capacity
|
||||
end -= 1
|
||||
return self._reduce_helper(start, end, 1, 0, self._capacity - 1)
|
||||
|
||||
def __setitem__(self, idx, val):
|
||||
# index of the leaf
|
||||
idx += self._capacity
|
||||
self._value[idx] = val
|
||||
idx //= 2
|
||||
while idx >= 1:
|
||||
self._value[idx] = self._operation(
|
||||
self._value[2 * idx],
|
||||
self._value[2 * idx + 1]
|
||||
)
|
||||
idx //= 2
|
||||
|
||||
def __getitem__(self, idx):
|
||||
assert 0 <= idx < self._capacity
|
||||
return self._value[self._capacity + idx]
|
||||
|
||||
|
||||
class SumSegmentTree(SegmentTree):
|
||||
def __init__(self, capacity):
|
||||
super(SumSegmentTree, self).__init__(
|
||||
capacity=capacity,
|
||||
operation=operator.add,
|
||||
neutral_element=0.0
|
||||
)
|
||||
|
||||
def sum(self, start=0, end=None):
|
||||
"""Returns arr[start] + ... + arr[end]"""
|
||||
return super(SumSegmentTree, self).reduce(start, end)
|
||||
|
||||
def find_prefixsum_idx(self, prefixsum):
|
||||
"""Find the highest index `i` in the array such that
|
||||
sum(arr[0] + arr[1] + ... + arr[i - i]) <= prefixsum
|
||||
|
||||
if array values are probabilities, this function
|
||||
allows to sample indexes according to the discrete
|
||||
probability efficiently.
|
||||
|
||||
Parameters
|
||||
----------
|
||||
perfixsum: float
|
||||
upperbound on the sum of array prefix
|
||||
|
||||
Returns
|
||||
-------
|
||||
idx: int
|
||||
highest index satisfying the prefixsum constraint
|
||||
"""
|
||||
assert 0 <= prefixsum <= self.sum() + 1e-5
|
||||
idx = 1
|
||||
while idx < self._capacity: # while non-leaf
|
||||
if self._value[2 * idx] > prefixsum:
|
||||
idx = 2 * idx
|
||||
else:
|
||||
prefixsum -= self._value[2 * idx]
|
||||
idx = 2 * idx + 1
|
||||
return idx - self._capacity
|
||||
|
||||
|
||||
class MinSegmentTree(SegmentTree):
|
||||
def __init__(self, capacity):
|
||||
super(MinSegmentTree, self).__init__(
|
||||
capacity=capacity,
|
||||
operation=min,
|
||||
neutral_element=float('inf')
|
||||
)
|
||||
|
||||
def min(self, start=0, end=None):
|
||||
"""Returns min(arr[start], ..., arr[end])"""
|
||||
|
||||
return super(MinSegmentTree, self).reduce(start, end)
|
||||
|
||||
```
|
||||
## 六、总结与展望
|
||||
虽然PER在采用**相同的交互次数**时会获得更高的性能，更加适合**稀疏奖励**或者**高奖励难以获得**的复杂环境，但其花费同样的时间，性能不一定更高，即花的时间要多三四倍。（参考文献6）针对PER耗时问题提出自己的实验和结论，其将总采样消耗的时间划分为三个部分（**采样时间、PER更新时间、算法更新时间**）进行实验，发现添加了原始PER的网络耗时反而更高。
|
||||
|
||||
> The first one is the sample, which needs to search on the sum-tree. When the capacity of EM goes larger, the sampling time, whose time complexity is O(logN), becomes a bottleneck.
|
||||
The second one is PER update, which is the same time complexity as sampling.
|
||||
The last one is the DDQN or DDPG update, which is executed on GPU.
|
||||
We measure the time cost to correct all priorities of EM(capacity is 106). All data must be predicted by DDQN on GPU, it needs 150+ s. We can see that the update cost is very high.
|
||||
|
||||
同时笔者本人及导师在实验时也发现了同样的问题，PER对于目前稀疏奖励环境，理论上应该是有成效，但由于现阶段大家为了更快探索，更快收敛，不仅在环境感知层面做了不少trick，奖励函数也设计得越来越丰富，PER耗时长的缺点被无限放大，故而大家在选择经验回放池的时候尽可能考虑自己的实际情况，不要拿着Rainbow算法就开始魔改，效果可能会适得其反。
|
||||
## 参考文献
|
||||
1.[https://arxiv.org/pdf/1511.05952.pdf](https://arxiv.org/pdf/1511.05952.pdf)
|
||||
|
||||
2.[https://zhuanlan.zhihu.com/p/310630316](https://zhuanlan.zhihu.com/p/310630316)
|
||||
|
||||
3.[https://zhuanlan.zhihu.com/p/160186240](https://zhuanlan.zhihu.com/p/160186240)
|
||||
|
||||
4.[https://zhuanlan.zhihu.com/p/137880325](https://zhuanlan.zhihu.com/p/137880325)
|
||||
|
||||
5.[https://jaromiru.com/2016/11/07/lets-make-a-dqn-double-learning-and-prioritized-experience-replay/](https://jaromiru.com/2016/11/07/lets-make-a-dqn-double-learning-and-prioritized-experience-replay/)
|
||||
|
||||
6.[https://www.mdpi.com/2076-3417/10/19/6925/pdf](https://www.mdpi.com/2076-3417/10/19/6925/pdf)
|
||||
|
||||
7.[蘑菇书EasyRL](https://gitcode.net/mirrors/datawhalechina/easy-rl?utm_source=csdn_github_accelerator)
|
||||
|
||||
## 个人简介
|
||||
|
||||
李成阳
|
||||
|
||||
|
||||
|
||||
@@ -0,0 +1,306 @@
|
||||
## JOYRL论文阅读<Rainbow: Combining Improvements in Deep Reinforcement Learning>
|
||||
|
||||
作者：Hessel, M., Modayil, J., Van Hasselt, H., Schaul, T., Ostrovski, G., Dabney, W., ... & Silver, D.
|
||||
|
||||
实验室：Google DeepMind
|
||||
|
||||
论文地址：https://arxiv.org/pdf/1710.02298
|
||||
|
||||
发表： In *Thirty-second AAAI conference on artificial intelligence*.
|
||||
|
||||
## 1 摘要
|
||||
|
||||
### 1.1 摘要--背景及问题
|
||||
|
||||
从DQN<sup><a href="#ref1">1</a></sup>推导过程中发现依旧存在很多问题，常见的改进措施Double DQN<sup><a href="#ref1">2</a></sup>、Dueling DQN<sup><a href="#ref1">3</a></sup>、Prioritized replay<sup><a href="#ref1">4</a></sup>、Multi-step<sup><a href="#ref1">5</a></sup>、Distributional RL<sup><a href="#ref1">6</a></sup>、Noisy Net<sup><a href="#ref1">7</a></sup>等方法，这些方法并不是完全独立，比如在Dueling中其实已经将Double DQN和Prioritized replay结合起来。
|
||||
|
||||
### 1.2 摘要--方法
|
||||
|
||||
本文希望将上述六种DQN方法结合经验融合在一起，来得到一个更好的网络。
|
||||
|
||||
### 1.3 摘要--贡献
|
||||
|
||||
1. 成为Atari 2600中SOTA(State-of-the-art)
|
||||
2. 我们还提供详细的消融研究的结果，该研究结果显示了每个组件对整体性能的贡献。
|
||||
|
||||
## 2 问题背景
|
||||
|
||||
### 2.1 RL problem & 记号
|
||||
|
||||
强化学习希望一个具有动作(Action)的智能体(Agent) 在与环境(Environment)交互的过程可以最大化奖励(Reward)，在这个过程中并不会直接监督式的学习。这里分享另外一种定义:
|
||||
|
||||
> 一、Mathematical formalism for learning- based decision making
|
||||
>
|
||||
> 二、Approach for learning decision-making and control from experience
|
||||
|
||||
**MDP (Markov Decision Process) $\{S,A,T,r,\gamma\}$ **
|
||||
|
||||
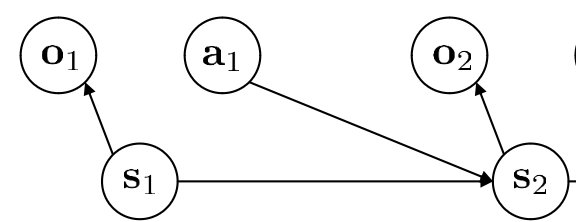
在不同的时间步下$t=0,1,2,..$，环境状态$S_t$提供给智能体一个观测信息$O_t$，通常我们会认为是完全观测(即$S_t=O_t$)，同时智能体根据观测信息做出动作$A_t$，之后环境给出下一个奖励$R_{t+1}$，奖励的折扣$\gamma_{t+1}$以及更新状态为$S_{t+1}$
|
||||
|
||||
|
||||
|
||||
在这个过程通常$S,A$是有限的情况，对于环境来说状态转移 (Stochastic transition function)、奖励方程包括
|
||||
|
||||
$$T(s,a,s')=P[S_{t+1=s'}|S_t=s,A_t=a]$$
|
||||
|
||||
$$r(s,a)=E[R_{t+1}|S_t=s,A_t=a]$$
|
||||
|
||||
对于智能体来说，根据状态$S_t$（或者完全观测下的观测$O_t$)得到得到动作$A_t$来自于策略$\pi$（Policy)，在序列决策中我们的目标是最大化某个状态采取某个动作的折扣奖励之和
|
||||
|
||||
$$P(A_t=a)=\pi_{\theta}[A_t=a|S_t=s]$$
|
||||
|
||||
$$max G_t=\Sigma_{k=0}^{\infty}r_t^{k}R_{t+k+1}$$
|
||||
|
||||
我们在利用算法进行梯度提升通常会经过三个步骤：
|
||||
|
||||
1. 生成样本
|
||||
2. 评估模型或者是计算回报
|
||||
3. 提升策略
|
||||
|
||||
### 2.2 Policy Gradient：直接提升策略
|
||||
|
||||
为了最大化策略的回报，我们可以直接对$G_t$最大化（即REINFRORCEMENT算法）
|
||||
|
||||
|
||||
|
||||
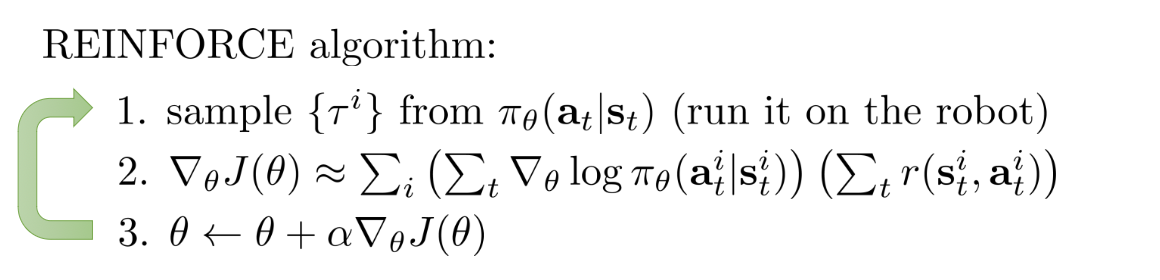
我们可以利用Baseline、N-steps、Discount、Importance sampling等技巧对算法进行改进。
|
||||
|
||||
### 2.3 **Actor-Crtic方法**：评估汇报(Estimate return)与提升策略分开
|
||||
|
||||
也可以引入新的状态价值函数$V^{\pi}(s)$来结合拟合的方式计算$G_t$之后最大化(A3C)，也可以直接利用 $V^{\pi}(s)$和动作状态价值函数$Q^{\pi}(s,a)$来进行基于价值函数的学习方法。
|
||||
|
||||
$$V^{\pi}(s)=E_{\pi}[G_t|S_t=s]$$
|
||||
|
||||
$$Q^{\pi}(s,a)=E_\pi[G_t|S_t=s,A_t=a]$$
|
||||
|
||||
|
||||
|
||||
我们可以利用回放池(Replay buffer)、神经网络来学习降低策略梯度中的方差。
|
||||
|
||||
### 2.4 Value-based method 抛弃策略
|
||||
|
||||
Policy iteration->Value iteration->Q learning
|
||||
|
||||
首先从策略迭代与价值迭代说起，[参考链接](https://hrl.boyuai.com/chapter/1/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%AE%97%E6%B3%95)可以看作是利用动态规划的方式反应强化学习的过程，两者的区别在于反应的是贝尔曼期望还是贝尔曼最优。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
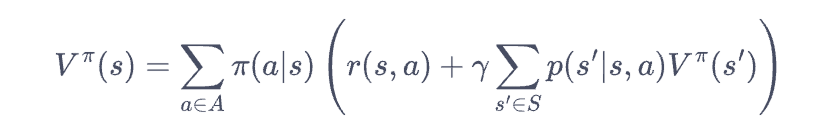
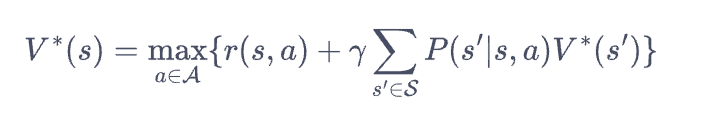
在基于价值学习算法的过程中，优点是我们只需要一个经验回放池，只需要$(s,a,s',r)$而不是需要完整的决策序列。我们通常会引入随机探索（Exploration）的概念，常见的包括$\epsilon-Greedy$的方法，在一定概率下选择非策略产生的动作。
|
||||
|
||||
|
||||
|
||||
在价值迭代的基础上，我们可以抛弃对$V(s)$的学习，而只是记录$Q(s,a)$; Q-iteration algorithm (或者$Q-learning$)的过程如下图所示
|
||||
|
||||
|
||||
|
||||
### 2.5 DQN推导
|
||||
|
||||
在上述我们认识对于MDP目标，从显式表达策略，到结合状态价值再到之后的完全使用价值函数来使用学习的方法，我们仍然没有解决的问题包括
|
||||
|
||||
1. 状态-动作空间的连续性
|
||||
2. 在状态空间和动作空间纬度大的时候无法准确刻画 状态-动作价值
|
||||
|
||||
随着神经网络的发展，我们希望利用网络拟合的方式来解决上述问题，同时每一步利用$\epsilon-Greedy$的方式来探索回放池中的经验，并利用梯度下降等方法最小化价值函数表达的回报
|
||||
|
||||
$$min (R_{t+1}+\gamma_{t+1}max_{a'}(S_{t+1},a')-q_{\theta}(S_t,A_t))^2$$
|
||||
|
||||
* 1 初始化大小为$N$的经验回放池 (PS：注意有大小限制)
|
||||
* 2 用相同随机的网络参数初始化 $Q_{\theta}(s,a)$ 与目标网络 $Q_{\theta'}(s,a)$
|
||||
* 3 FOR 回合 = 1，N DO：
|
||||
* 4 获取环境初始状态 $s_1$
|
||||
* 5 FOR 时间步 = 1，T DO：
|
||||
* 6 根据当前网络$a_t=max_a Q_{\theta}(s,a)$结合$\epsilon-Greedy$方法来得到$a_t$（PS：注意这一步动作的确定隐含之后DQN回报偏大的特点）
|
||||
* 7 执行动作$a_t$,获取$r_t$,环境状态变为$s_{t+1}$
|
||||
* 8 存储上述采样信息到经验回放池
|
||||
* 9 if 经验回放池数目足够：
|
||||
* 10 采样batchsize个样本$\{s_t^i,a_t^i,r_t^i,s_{t+1}^i\}$
|
||||
* 11 计算目标值$y^i_t=r^i_t+\gamma*max_aQ_{\hat \theta}(s^i_{t+1},a^i_t)$
|
||||
* 12 最小化损失函数$L=\frac{1}{N}(y_t^i-Q_{\theta}(s_t^i,a_t^i))^2$
|
||||
* 13 更新网络参数
|
||||
* 14 END FOR
|
||||
* 15 更新目标网络参数
|
||||
* 16 END FOR
|
||||
|
||||
|
||||
|
||||
其中非常有趣的技巧包括：
|
||||
|
||||
1. 经验回放(Experience replay)与随机探索；这一部分主要是为了提高样本采样效率，同时降低后续梯度下降中样本的相关性。
|
||||
2. 目标网络(Target network)；由于TD误差在策略改变过程中也会改变，因此造成神经网络拟合过程的不稳定性，因此构建新的目标网络，在每次迭代过程中暂时固定，在回合结合后更新参数，这样需要两层Q网络。
|
||||
|
||||
[相关代码实现](https://paperswithcode.com/paper/playing-atari-with-deep-reinforcement)
|
||||
|
||||
|
||||
|
||||
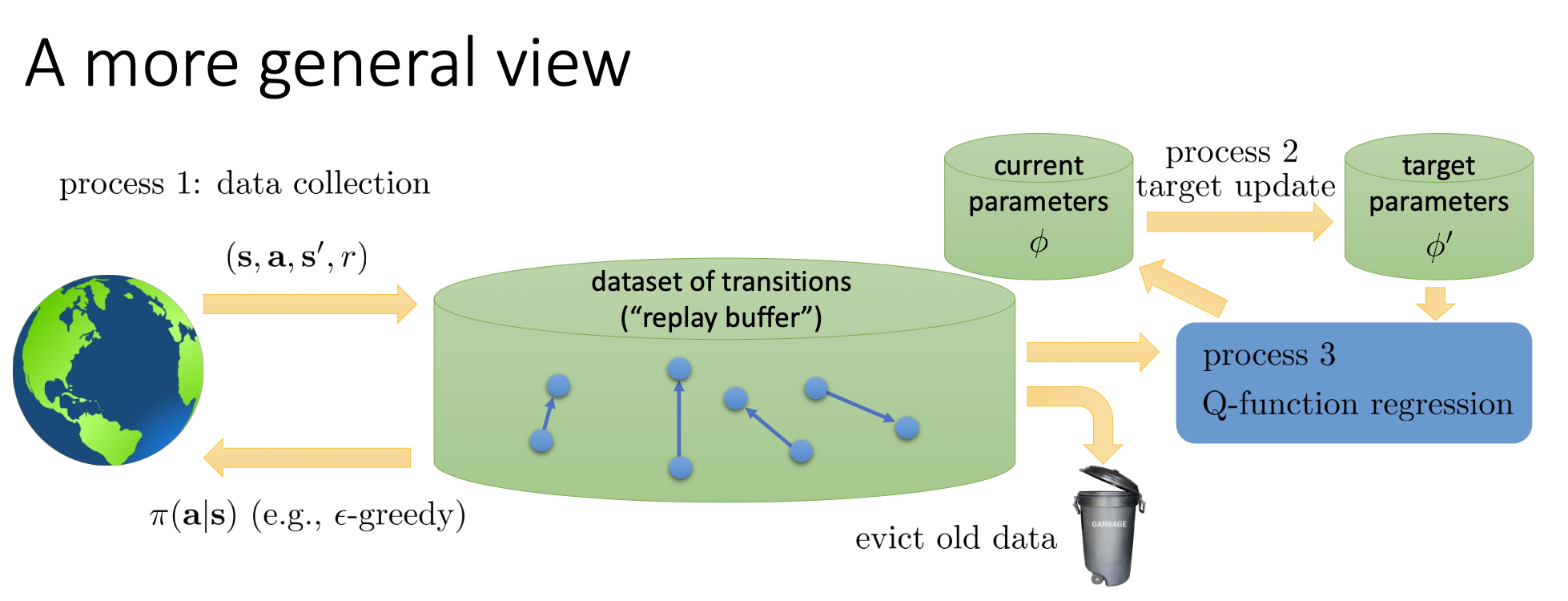
## 3 DQN改进
|
||||
|
||||
虽然DQN成功让强化学习在某些方面超过人类，但是依旧有这许多限制。
|
||||
|
||||
### 3.1 改进1：Double Q- Learning
|
||||
|
||||
在DQN中会有估计值过高的情况，证明如下：
|
||||
|
||||
$$target-value:y^i_t=r^i_t+\gamma max_{a_{t+1}^i}Q_{\hat \theta}(S^i_{t+1},a^i_{t+1})$$
|
||||
|
||||
$$max_{a_{t+1}^i}Q_{\hat \theta}(S^i_{t+1},a^i_{t+1})=Q_{\hat \theta}(s_{t+1}^i,argmax_{a_{t+1}^i}Q_{\hat \theta}(s_{t+1}^i,a_{t+1}^i))$$
|
||||
|
||||
根据期望公式
|
||||
|
||||
$$E[max(X1,X2)]>max(E(X1),E(X2))$$
|
||||
|
||||
|
||||
|
||||
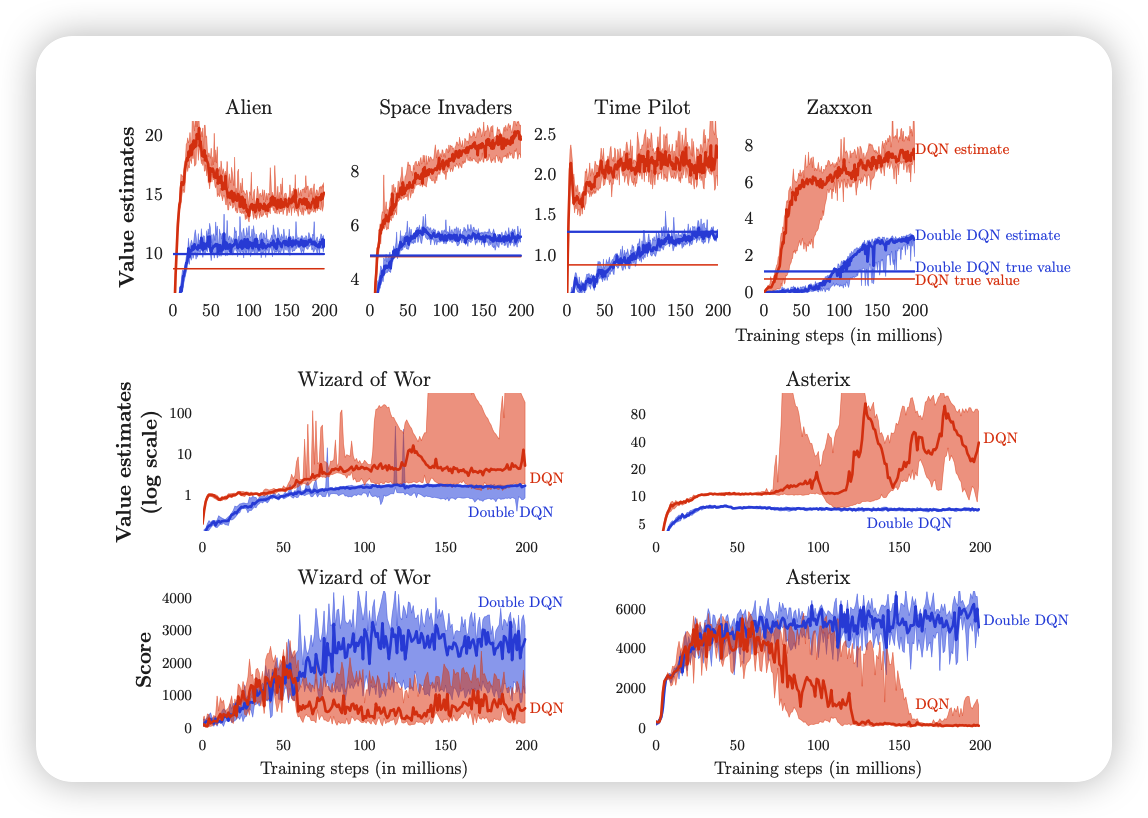
我们通过证明发现估计值较大的原因是因为我在模型选择行为和计算Q值使用同一个网络，如果降低行为选择和Q值计算的相关性就可以降低高估，因此直觉的我们可以设计两个网络
|
||||
|
||||
$$Q_{\theta_A}(s,a)=r+\gamma Q_{\theta_b}(s',a')$$
|
||||
|
||||
$$Q_{\theta_B}(s,a)=r+\gamma Q_{\theta_a}(s',a')$$
|
||||
|
||||
我们的确可以新加一个网络，但是会增加学习难度，需要重新设计架构。所以为什么不直接使用$Q_{\theta}(s,a)$作为行为的估计？
|
||||
|
||||
$$(target\_value\_double\_Q-learning):y^i_t=r^i_t+\gamma Q_{\hat \theta}(s^i_{t+1},argmax_{r^i_{t+1}Q_{\theta}}(s^i_{t+1},a^i_{t+1}))$$
|
||||
|
||||
### 3.2 改进2：Prioritized replay
|
||||
|
||||
在DQN学习中为高效利用$(s,a,r,s)$样本，我们会使用经验回放的方式来存储一定规模的样本，在梯度下降的时候通常是从经验回放中均匀采样（Uniformly sampling）来进行学习，但是我们依旧会存在两个问题：
|
||||
|
||||
1. 依旧没有完全解决数据之间独立同分布的假设
|
||||
2. 容易忘记一些罕见的、重要的经验数据
|
||||
|
||||
在该论文中作者首先制定指标“TD-error”作为衡量$(s_t^i,a_t^i,r_t^i,s^i_{t+1})$的信息量大小，作为采样的优先级，同时利用随机优先级采样、偏置和重要性采样等方式来避免贪心的问题。优先级的获取有3.2.1和3.2.2两种方式
|
||||
|
||||
$$(随机采样)P(i)=\frac{p_i^\alpha}{\Sigma_kP_k^\alpha}$$
|
||||
|
||||
### 3.2.1 比例优先级（Proportional prioritization）
|
||||
|
||||
$$P_i=|\sigma_i|+\epsilon$$
|
||||
|
||||
### 3.2.2 基于排名的优先级(Rank-based prioritization)
|
||||
|
||||
$$P_i=\frac{1}{rank(i)}$$；优点可以保证线性性质，对异常值不敏感。
|
||||
|
||||
上述两种是不同得到重要性的方式；在实现时候采用Sum-tree的数据结构降低算法复杂程度。在采样中考虑重要性采样(Importance sampling)，并由此来进行热偏置(Annealing the bias）来修正误差
|
||||
|
||||
$$w_j=(\frac{1}{N}*\frac{1}{P(i)})^\beta$$
|
||||
|
||||
|
||||
|
||||
### 3.3 改进3：Dueling networks
|
||||
|
||||
Dueling DQN是一种针对基于价值函数的强化学习的网络结构设计，其并不直接输出状态动作价值函数，而是输出状态价值函数与动作状态优势函数，因为通常会共用前几层的卷积参数，在后面则是状态价值函数与优势函数各自的参数。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
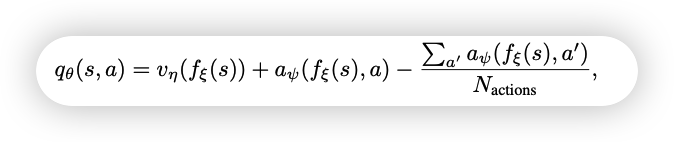
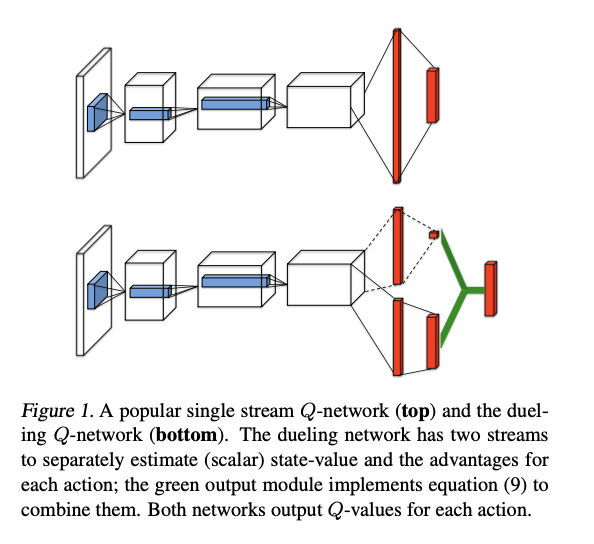
### 3.4 改进4：Multi-step learning
|
||||
|
||||
在对状态动作函数的优势估计时候，通常我们会分为蒙特卡洛方法与Bootstrap(或者是Actor- critic内的C)的方法
|
||||
|
||||
$$(MC-sampling)A_t=\Sigma_{k=0}^{\infty}\gamma_t^{k}（R_{t+k+1}-b)$$
|
||||
|
||||
$$(bootstrap-sampling)G_t=r_{t}+\gamma*V(s_{t+1})-V(s_t)$$
|
||||
|
||||
前者方法偏差低但是方差较大；后者方差低但是有偏。因此结合两者我们通常会有Multi-step target的方法。
|
||||
|
||||
|
||||
|
||||
同样的也可以用在DQN中对于状态动作价值函数的估计：
|
||||
|
||||
$$R_t^{n}=\Sigma_{k=0}^{n-1}\gamma_t^{k}R_{t+k+1}$$
|
||||
|
||||
更新之后的损失函数为
|
||||
|
||||
$$(R_t^{n}+\gamma_t^nmax_{a'}Q_{\hat \theta}(S_{t+n},a')-Q_\theta(S_t,A_t))^2$$
|
||||
|
||||
### 3.5 改进5：Distributional RL
|
||||
|
||||
在基于价值函数的学习中我们通常是返回一个期望或者最大值而丢失很多其他信息，因此Distributional RL尝试利用其分布而不是单个值来进行强化学习。首先本文尝试将价值函数范围$[V_{min},V_{max}]$划分为N个各自来估计价值函数，利用Boltzmann分布表示价值函数的分布，同时利用投影的操作
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
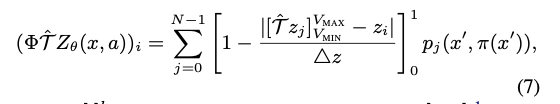
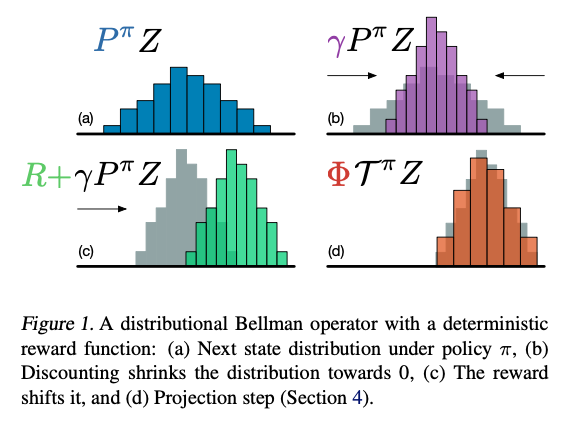
由此对于分布拟合可以划分为交叉熵的形式，算法流程
|
||||
|
||||
|
||||
|
||||
### 3.6 改进6：Noisy Nets
|
||||
|
||||
在Q- learning或者是DQN中，我们的轨迹并不是完全采样的，而是与我们的探索策略相关，最原本的是$\epsilon-Greedy$策略，这里提出一种NoisyNet来对参数增加噪声来增加模型的探索能力
|
||||
|
||||
$$y=(Wx+b)+(b_{noisy}\odot\epsilon^b+W_{noisy}\odot\epsilon^w)x$$
|
||||
|
||||
噪声的生成可以分为Independent Gaussian noise；Factorised Gaussian noise两种方式。
|
||||
|
||||
|
||||
|
||||
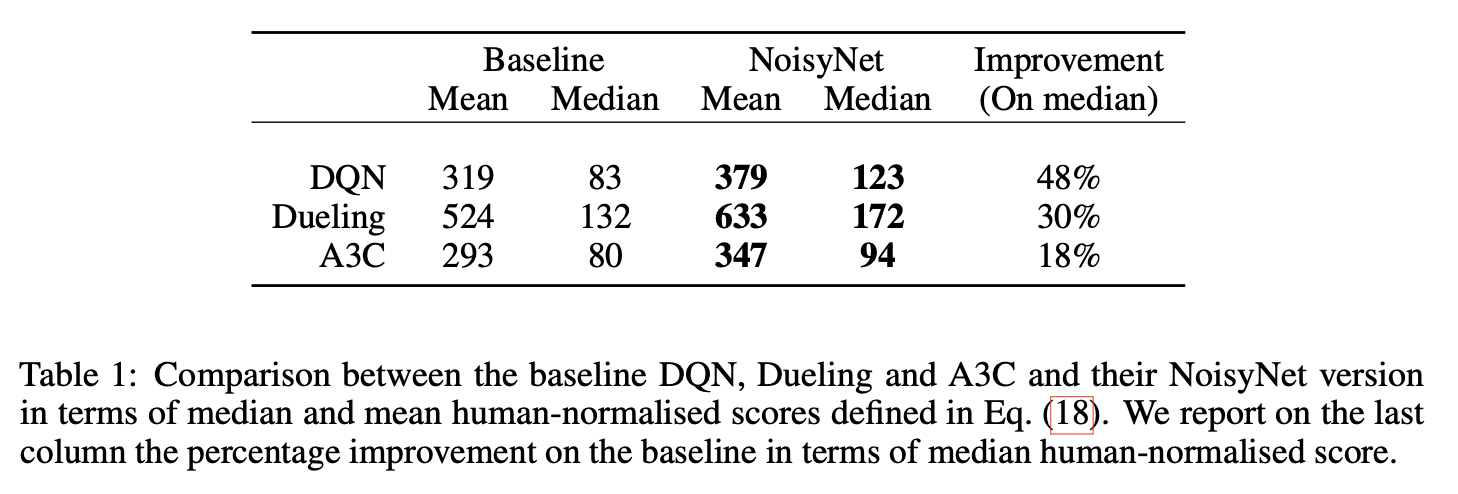
### 3.7 融合上述策略
|
||||
|
||||
首先将（改进5:Distributional RL）中的损失函数更换称为（改进4:Multi-step learning），并利用（改进1--Double Q- Learning）计算新的目标值
|
||||
|
||||
$$d_t^n=(R_t^n+r_t^nz,p_\hat\theta(S_{t+n},a^*_{t+n}))$$
|
||||
|
||||
损失函数为
|
||||
|
||||
$$D_{KL}(\Phi_zd_t^n||d_t)$$
|
||||
|
||||
同时在采样过程中我们通常会减少TD-error，而在本文中我们的损失函数为KL损失，因此我们的（改进2：Prioritized replay）中的优先级定义为
|
||||
|
||||
$$p_t\propto (D_{KL}(\Phi_zd_t^n||d_t))^w$$
|
||||
|
||||
同时改变（改进3: Dueling networks）由接受期望转向接受价值函数分布，最后更改所有的线性层更换为（改进6：Noisy Nets）
|
||||
|
||||
$$p_\theta(s,a)^i=\frac{exp(v^i_\eta(\phi)+a^i_\psi(\phi,a)-\hat a_\psi^i(s))}{\Sigma_j exp(v^j_\eta(\phi)+a^j_\psi(\phi,a)-\hat a_\psi^j(s)) }$$
|
||||
|
||||
## 4 实验
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
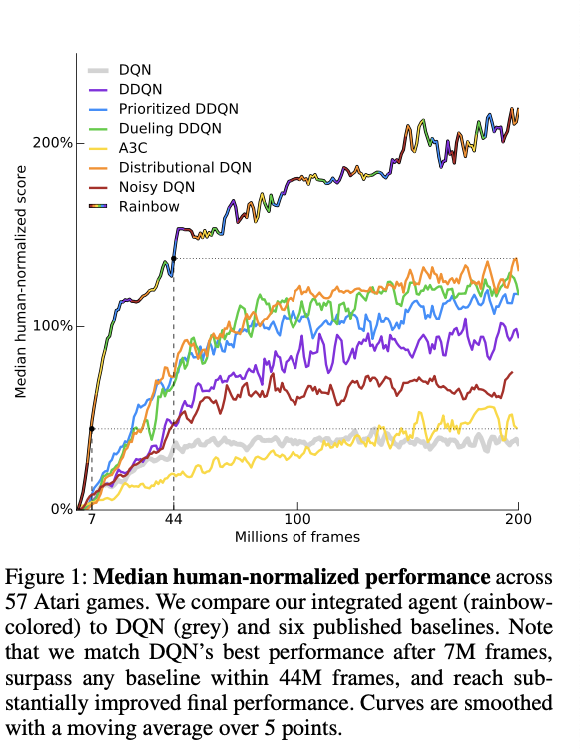
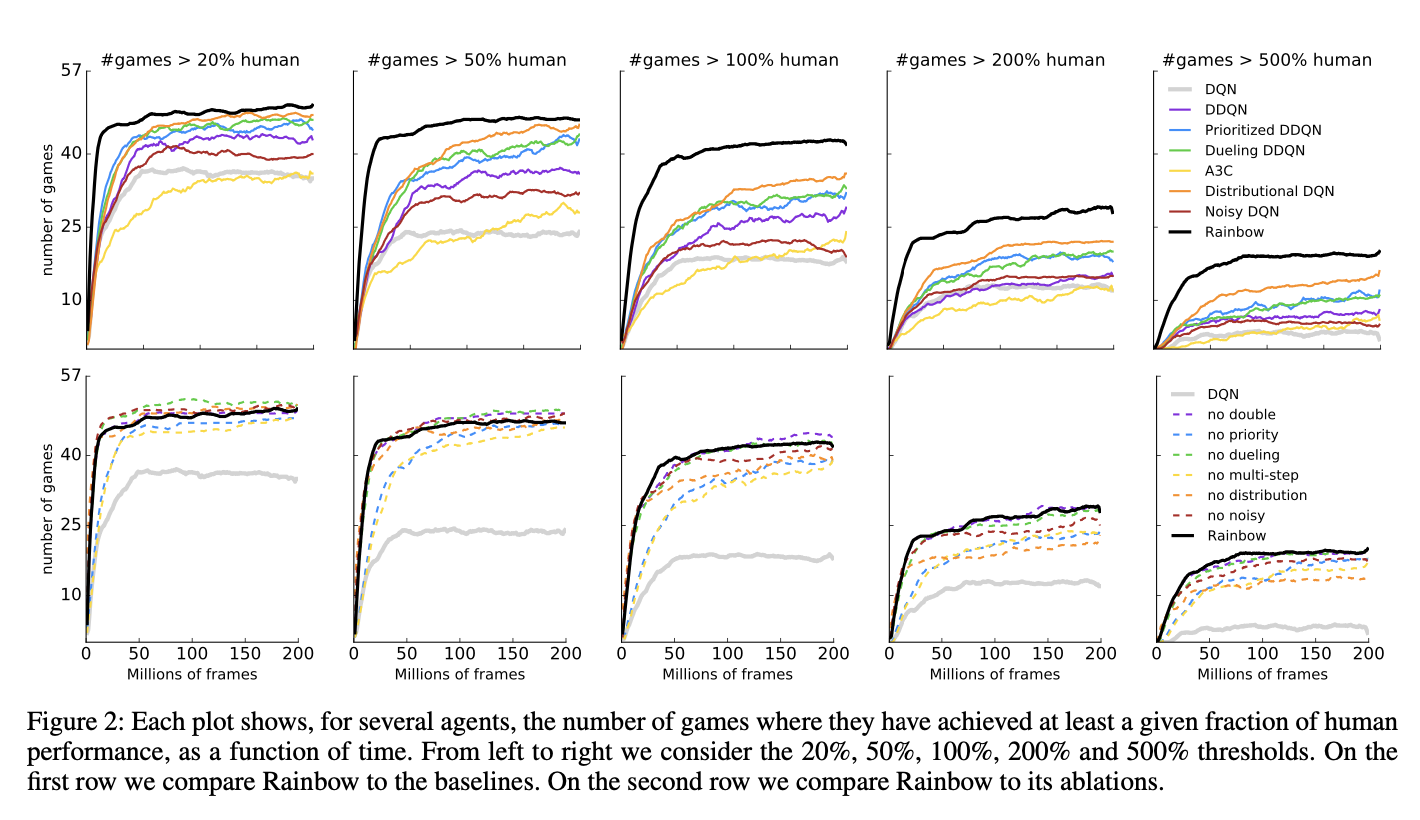
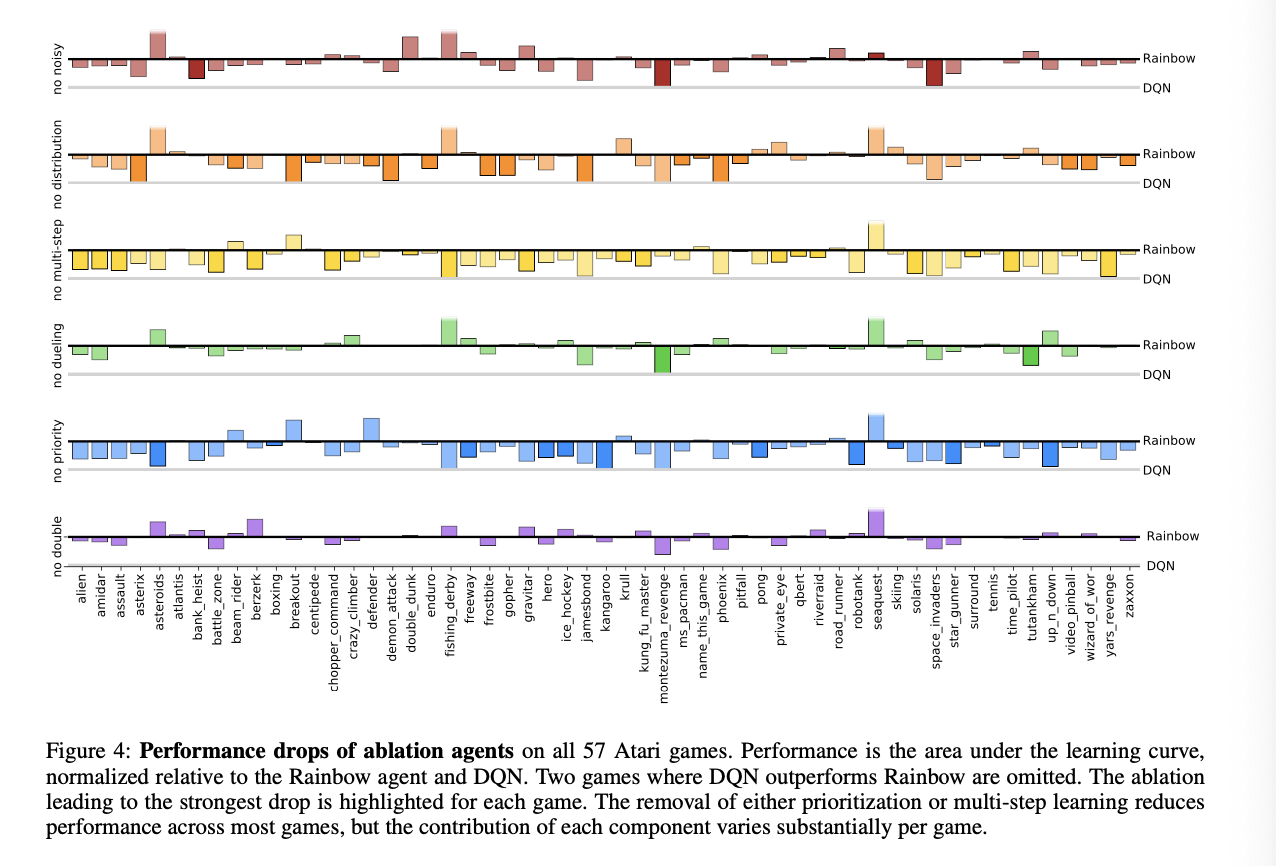
## 5 总结
|
||||
|
||||
### 5.1 结论
|
||||
|
||||
1. Rainbow相比较其他现有的算法要更好，速度也会更快
|
||||
2. 在消融实验中；我们会发现（改进2：Prioritized replay）与（改进4:Multi-step learning）会造成结果中位数大幅度下降;(改进5:Distributional RL)在最开始表现良好，但是最终结果表现较差；同时（改进6：Noisy Nets）通常会有更好的中位数表现，同时由于本次状态中通常是underestimate的，所以（改进1--Double Q- Learning）效果并不显著，（改进3: Dueling networks）提升幅度不大。
|
||||
|
||||
### 5.2 讨论
|
||||
|
||||
作者在最后总结他们的工作，主要是从Value- based的Q-learning方法集合中寻找，而没有考虑Purely policy- based的算法（比如TRPO)，本文从网络探索、网络初始化、数据使用、损失或函数等方面进行集合，与之相对应的同样有很多工作，未来还可以用很多其他的方法。但是
|
||||
|
||||
> In general, we believe that exposing the real game to the agent is a promising direction for future research.
|
||||
|
||||
### 5.3 个人感悟
|
||||
|
||||
这篇论文的观点很直接，在实际实现的过程中作者做了很多Dirty work，尝试过很多次，并最终证明集成的方式是有效的，以及分析哪些技巧是有效的、哪些技巧是欠佳的，工作量非常大！
|
||||
|
||||
|
||||
|
||||
【1】<span name = "DQN">[Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. *arXiv preprint arXiv:1312.5602*.](https://arxiv.org/abs/1312.5602)</span>
|
||||
|
||||
【2】<span name = "DDQN">[Van Hasselt, H., Guez, A., & Silver, D. (2016, March). Deep reinforcement learning with double q-learning. In *Proceedings of the AAAI conference on artificial intelligence* (Vol. 30, No. 1).](http://arxiv.org/abs/1509.06461)</span>
|
||||
|
||||
【3】 <span name = "Prioritized experience replay"> [Schaul, T., Quan, J., Antonoglou, I., & Silver, D. (2015). Prioritized experience replay. *arXiv preprint arXiv:1511.05952*.](https://arxiv.org/abs/1511.05952)</span>
|
||||
|
||||
【4】<span name = "Multistep">[Multi Step Learning](https://www.cs.mcgill.ca/~dprecup/courses/RL/Lectures/8-multistep-2019.pdf)</span>
|
||||
|
||||
【5】<span name = "Dueling">[Wang, Z., Schaul, T., Hessel, M., Hasselt, H., Lanctot, M., & Freitas, N. (2016, June). Dueling network architectures for deep reinforcement learning. In *International conference on machine learning* (pp. 1995-2003). PMLR.](https://arxiv.org/abs/1511.06581)</span>
|
||||
|
||||
【6】<span name = "Distributional">[Bellemare, M. G., Dabney, W., & Munos, R. (2017, July). A distributional perspective on reinforcement learning. In *International Conference on Machine Learning* (pp. 449-458). PMLR.](https://arxiv.org/pdf/1707.06887.pdf)</span>
|
||||
|
||||
【7】<span name = "NoisyDQN">[Fortunato, M., Azar, M. G., Piot, B., Menick, J., Osband, I., Graves, A., ... & Legg, S. (2017). Noisy networks for exploration. *arXiv preprint arXiv:1706.10295*.](https://arxiv.org/abs/1706.10295)</span>
|
||||
|
||||
### 自我介绍
|
||||
|
||||
非典型INFJ，一枚普通985的交通信息方向2022级硕士生，主要研究方向为交通数据分析、组合优化等，在学习的路上希望自己可以保持“求知若饥，虚心若愚”。可以在blog.tjdata.site找到我。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
BIN
papers/DQN/img/Double_1.png
Normal file
BIN
papers/DQN/img/Double_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 13 KiB |
BIN
papers/DQN/img/Double_2.png
Normal file
BIN
papers/DQN/img/Double_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 90 KiB |
BIN
papers/DQN/img/Double_3.png
Normal file
BIN
papers/DQN/img/Double_3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 143 KiB |
BIN
papers/DQN/img/Dueling_1.png
Normal file
BIN
papers/DQN/img/Dueling_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 67 KiB |
BIN
papers/DQN/img/Dueling_2.png
Normal file
BIN
papers/DQN/img/Dueling_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 39 KiB |
BIN
papers/DQN/img/Dueling_3.png
Normal file
BIN
papers/DQN/img/Dueling_3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 75 KiB |
BIN
papers/DQN/img/PlayingAtari_1.png
Normal file
BIN
papers/DQN/img/PlayingAtari_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 115 KiB |
BIN
papers/DQN/img/PlayingAtari_2.png
Normal file
BIN
papers/DQN/img/PlayingAtari_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 70 KiB |
@@ -0,0 +1,131 @@
|
||||
## A Distributional Perspective on Reinforcement Learning
|
||||
|
||||
作者：Marc G. Bellemare, Will Dabney, Rémi Munos
|
||||
|
||||
出处：DeepMind, ICML, 2017
|
||||
|
||||
论文链接：https://arxiv.org/abs/1707.06887
|
||||
|
||||
**亮点：作者提出了一种基于值分布的强化学习算法，将过去强化学习算法中对累计回报的期望进行建模改为对累计回报的分布进行建模，提出了一种新的算法，并做了实验验证，在Atari基准上超过了原有的算法**
|
||||
|
||||
### **Motivation (Why):**
|
||||
|
||||
基于值的强化学习算法只对累计回报的期望进行建模，关于分布的很多信息丢失了，如方差，分位数等信息。在风险规避的场景，更倾向于选择方差较小而不是一味地选择均值高的行为。
|
||||
|
||||
### **Main Idea (What):**
|
||||
|
||||
将原有的贝尔曼算子改为分布式贝尔曼算子，并给出了相关性质的证明，将原有的价值函数在期望上收敛到一个固定数值的理论，改为了一套关于价值函数在分布上收敛到一个固定的理论。
|
||||
|
||||
**贝尔曼方程**
|
||||
|
||||
经典的基于价值的强化学习方法尝试使用期望值对累积回报进行建模，表示为价值函数$V(x)$ 或动作价值函数 $Q(x,a)$，然后智能体把价值函数当成“地图”，根据指引选择不同状态下的行为。强化学习通常使用贝尔曼方程来描述价值函数
|
||||
$$
|
||||
\begin{aligned}
|
||||
&Q^\pi(x, a):=\mathbb{E} Z^\pi(x, a)=\mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^t R\left(x_t, a_t\right)\right] \\
|
||||
&x_t \sim P\left(\cdot \mid x_{t-1}, a_{t-1}\right), a_t \sim \pi\left(\cdot \mid x_t\right), x_0=x, a_0=a
|
||||
\end{aligned}
|
||||
$$
|
||||
其中，$Z^\pi$ 表示回报是沿着智能体在策略 $\pi$ 下与环境互动的轨迹所获得的折扣奖励的总和。策略 $\pi$ 的价值函数 $Q^\pi$ 描述了从状态 $x \in X$ 采取动作 $a \in A$ ，然后根据 $\pi$ 获得的期望回报。贝尔曼方程也可以被改写成如下迭代形式:
|
||||
$$
|
||||
Q^\pi(x, a)=\mathbb{E} R(x, a)+\gamma \underset{P, \pi}{\mathbb{E}} Q^\pi\left(x^{\prime}, a^{\prime}\right)
|
||||
$$
|
||||
在强化学习中，我们通常感兴趣的是采取动作使回报最大化。最常见的方法是使用最优方程:
|
||||
$$
|
||||
Q^*(x, a)=\mathbb{E} R(x, a)+\gamma \mathbb{E}_P \max _{a^{\prime} \in \mathcal{A}} Q^*\left(x^{\prime}, a^{\prime}\right) .
|
||||
$$
|
||||
该方程具有唯一的不动点 $\mathrm{Q}^*$ ，即最优价值函数，对应于最优策略集 $\pi^*\left(\right.$ 当 $\mathbb{E}_{a \sim \pi^*} Q^*(x, a)=\max _a Q^*(x, a)_{\text {时， }} \pi^*$ 是最优的 $)$ 。 我们将价值函数视为 $\mathbb{R}^{\mathcal{X} \times \mathcal{A}}$ 中的向量，并将期望奖励函数也视为这样的向量。在这种情况下，Bellman算子和最优算子T定义如下:
|
||||
$$
|
||||
\begin{aligned}
|
||||
\mathcal{T}^\pi Q(x, a) &:=\mathbb{E} R(x, a)+\gamma \underset{P, \pi}{\mathbb{E}} Q\left(x^{\prime}, a^{\prime}\right) \\
|
||||
\mathcal{T} Q(x, a) &:=\mathbb{E} R(x, a)+\gamma \mathbb{E}_P \max _{a^{\prime} \in \mathcal{A}} Q\left(x^{\prime}, a^{\prime}\right)
|
||||
\end{aligned}
|
||||
$$
|
||||
这些算子非常有用，很多强化学习算法都建立于此。特别地，它们都是压缩映射，并且它们在某些初始$Q_0$上的重复应用收敛到$Q^pi$或$Q^*$。
|
||||
|
||||
**分布式贝尔曼方程**
|
||||
|
||||
以上贝尔曼方程是基于期望的贝尔曼方程，描述的是三个随机变量期望之间的关系，即$Q^\pi(x, a), \mathbb{E} R(x, a), \gamma \underset{P, \pi}{\mathbb{E}} Q^\pi\left(x^{\prime}, a^{\prime}\right)$。其中第一项后后两项的加和，故也为期望的形式。分布式贝尔曼方程，将随机变量的期望用随机变量本身来替代，即：
|
||||
$$
|
||||
Z(x, a)=R(x, a)+\gamma Z(X^{\prime}, A^{\prime})
|
||||
$$
|
||||
其中，$Z(x,a)$ 是表示 $(x, a)$下收益的随机变量，$R(x,a)$ 表示当前回报的随机变量,$\gamma Z(X^{\prime}, A^{\prime})$ 是关于下一状态折现后收益的随机变量，物理意义上没有变化。
|
||||
|
||||
值分布贝尔曼算子${T}^\pi$的更新公式：
|
||||
$$
|
||||
\begin{aligned}
|
||||
\mathcal{T}^\pi Q(x, a) &:=R(x, a)+\gamma P^\pi Z\left(x,a\right)
|
||||
\end{aligned}
|
||||
$$
|
||||
其中，
|
||||
$$
|
||||
\begin{aligned}
|
||||
&P^\pi Z\left(x,a\right) :\overset{D}{=} Z(X^{\prime}, A^{\prime})
|
||||
\\
|
||||
& X \sim P\left(\cdot \mid x, a\right), A^\prime \sim \pi\left(\cdot \mid X^\prime\right)
|
||||
\end{aligned}
|
||||
$$
|
||||
**对分布进行估计的优点：**
|
||||
|
||||
1. 很多时候均值不能反应分布特点
|
||||
2. 若不同行为期望相同，方差不同，仅仅考虑均值就不能做出正确选择。
|
||||
|
||||
### **Main Contribution (How):**
|
||||
|
||||
C51算法由两个重要的过程组成，参数化分布，投影贝尔曼更新。
|
||||
|
||||
**过程1：参数化分布**
|
||||
|
||||
在任何状态-动作对(x,a)处，累计折扣回报都是一个分布，在对这个分布进行表示上，C51采取了对随机变量空间离散化，再将随机变量建模为在这些离散空间上表示的加和，假设折扣累计回报$Z$的最大值为 $V_{M A X}$ ，最小值为 $V_{M I N}$ ，并将最小值与最大值之间的区间均匀离散化为 $\mathrm{N} 个$区间，则每个等分支集为 $\left\{z_i=V_{\min }+i \Delta z: 0 \leq i<N, \Delta z:=\frac{V_{M A X}-V_{M I N}}{N-1}\right\}$，支集为概率密度不为0的点。因此我们可以对支集上的概率分布进建模
|
||||
$$
|
||||
Z_{\theta}(x,a) = z_i \quad w.p. \quad p_i(x,a):=\frac{e^{\theta_i(x,a)}}{\sum_je^{\theta_j(x,a)}}
|
||||
$$
|
||||
其中w.p.为with probability的缩写。
|
||||
|
||||
|
||||
|
||||
上述图片参考自[知乎回答]([C51-值分布强化学习 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/337209047))，形象地表述出了C51算法将状态-动作对(x,a)输出至函数分布的过程
|
||||
|
||||
**过程2：投影贝尔曼更新**
|
||||
|
||||
|
||||
|
||||
<img src="img/C51_2.png" alt="2022-11-14 213502" style="zoom:67%;" />
|
||||
|
||||
(a)图中蓝色部分为下一个状态动作对的状态分布，经过折扣系数$\gamma$作用后变为(b)图中紫色部分，与常数随机变量回报相加后，平移后变为(c)图中映射部分。显然可以看出，值分布贝尔曼操作符是收缩的，故最终是可以收敛的。但同时会在值分布贝尔曼操作符一次又一次作用下离开原有的定义域，超出前文所述离散化的支集的范围，故我们需要一个映射$\phi$将更新后的随机变量投影到最开始的离散化支集上，这就是投影贝尔曼更新
|
||||
|
||||
**整体算法**
|
||||
|
||||
<img src="img/C51_3.png" alt="image-20221114205431206" style="zoom: 67%;" />
|
||||
|
||||
以上是C51算法整体的更新思想如下。将状态动作对映射到一个分布上去，然后一次一次迭代这个分布，使用Q-Learning的思想，将现有分布和更新后分布的差值当作损失，更新网络的参数，直到这个分布收敛到一个固定的分布。在这个过程中有以下难点：1.如何表示一个分布，2. 如何衡量两个分布的差值。过程1和过程2分别解决了这两个问题。
|
||||
|
||||
**结果：**
|
||||
|
||||
<img src="img/C51_4.png" alt="2022-11-14 230104" style="zoom:50%;" />
|
||||
|
||||
上图是不同数量固定区间的算法在不同任务下的表现，算法最终取名为C51是因为在消融实验后发现将概率分布表示为51各固定区间的概率加和后效果最佳。
|
||||
|
||||
<img src="img/C51_5.png" alt="2022-11-14 230144" style="zoom:67%;" />
|
||||
|
||||
Q函数在实验进行中一个时刻分布情况，图中可以明确看出各个动作的好坏
|
||||
|
||||
<img src="img/C51_6.png" alt="2022-11-14 230221" style="zoom:67%;" />
|
||||
|
||||
作者将C51与DQN，双重DQN，对偶结构DQN和优先回放DQN进行了比较， 比较训练期间取得的最优评估分数，发现C51明显优于其他算法。并且发现C51在许多游戏中（尤其是SEAQUEST）大大超越了当前的最新技术水平。一个特别引人注目的事实是该算法在稀疏奖励游戏有着卓越表现。
|
||||
|
||||
**本文提出方法的优点：**
|
||||
|
||||
1. C51算法的卷积神经网络的输出不再是行为值函数，而是支点处的概率，神经网络学习的目标由数值变为一个分布。可以使学到的内容除了数值以外的更多信息，即整个Q函数分布。
|
||||
2. C51在奖励稀疏的任务下表现更好，因为系数的奖励在分布式的传播中相对不容易丢失
|
||||
3. C51算法的框架虽然仍是DQN算法，但损失函数不再是均方差和，而是KL散度，可以更好地描述两个分布之间的差别。
|
||||
|
||||
### 个人简介
|
||||
|
||||
吴文昊，西安交通大学硕士在读，联系方式:wwhwwh05@qq.com
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
@@ -0,0 +1,147 @@
|
||||
# TD3: Addressing Function Approximation Error in Actor-Critic Methods 论文剖析
|
||||
|
||||
Scott Fujimoto, Herke van Hood, David Meger
|
||||
|
||||
|
||||
|
||||
## 一、文章信息
|
||||
|
||||
****
|
||||
|
||||
**Addressing Function Approximation Error in Actor-Critic Methods**
|
||||
|
||||
https://arxiv.org/abs/1802.09477
|
||||
|
||||
https://github.com/sfujim/TD3
|
||||
|
||||
|
||||
|
||||
## 二、写作动机
|
||||
|
||||
在Q-learning中，噪声源自函数逼近中无法避免的不精确估计。这种不精确估计在每次更新时被不断累加，并通过估计的最大化被不断估计为高值，导致高估问题（OverStimation）。作为DQN的拓展，DDPG在解决连续控制问题时也会存在高估问题。
|
||||
|
||||
本文借鉴Double DQN解决DQN中高估问题时的经验，解决连续动作控制问题中出现的高估问题。
|
||||
|
||||
|
||||
|
||||
## 三、相关工作
|
||||
|
||||
### 1. DDPG
|
||||
|
||||
DDPG解决了DQN不能用于连续控制的问题，采用基于DPG的Actor-Critic结构。其Actor部分采用估计网络 $\mu_\theta(s)$ 负责输出确定性动作，其目标网络与估计网络结构相同但参数不同，主要负责更新价值网络Critic；Critic部分负责价值函数 $Q_{\omega}(s,a)$ 的拟合，其估计网络以Actor估计网络的输出动作为输入，参与Actor和Critic的优化。目标网络Critic参与Critic优化时 $Q_{target}$ 的计算。
|
||||
|
||||
价值网络Critic的更新主要基于TD-error的梯度下降，具体更新公式如下：
|
||||
$$
|
||||
L_{critic}=\frac{1}{N}\sum_{i}(y_i-Q(s_i,a_i|\theta^{Q}))^2
|
||||
$$
|
||||
策略网络Actor的更新则是基于梯度上升，从而最大化价值网络输出的Q值，其更新公式如下：
|
||||
$$
|
||||
\nabla_{\theta^\mu}J \approx \frac{1}{N}\sum_i\nabla_aQ(s,a|\theta^Q)|_{s=s_i,a=\mu(s_i)} \nabla_{\theta^\mu}\mu(s|\theta^{\mu})|_{s_i}
|
||||
$$
|
||||
|
||||
|
||||
### 2. Double DQN
|
||||
|
||||
针对DQN中出现的高估问题，Double DQN使用两个独立的估计量来进行无偏估计。其将传统DQN中最优动作选取与最优动作价值函数计算进行解耦，采用目标网络 $\theta^-$ 与策略网络 $\theta$ 分别进行计算，具体计算形式如下：
|
||||
$$
|
||||
a^*=\substack{argmax\\{a \in \mathbb{A}}}Q(s,a|\theta_t^-)\\Y_t^Q=r+\gamma Q(S_t=s, A_t=a^*;\theta_t)
|
||||
$$
|
||||
通过减少traget的过估计，Double DQN减少了对动作价值函数的估计。
|
||||
|
||||
|
||||
|
||||
### 3. Averaged-DQN
|
||||
|
||||
Averaged-DQN提出了一种不同的高估问题解决方法，其聚焦于方差最小化，通过平均Q值来降低target近似方差（TAE），并且不同于Ensemble DQN，Averaged-DQN中采用最近K个版本的Q Function计算平均目标，通过采用过去的target network来避免K-Fold计算，获得更好的方差化简结果，对Variance的计算形式如下：
|
||||
$$
|
||||
Var[Q^A_i(s_0,a)]=\sum^{M-1}_{m=0}D_{K,m}\gamma^{2m}\sigma^2_{s_m}
|
||||
$$
|
||||
Averaged-DQN的计算公式如下：
|
||||
$$
|
||||
Q^A_N(s,a)=\frac{1}{K} \sum^{K-1}_{k=0}Q(s,a;\theta_{N-k})
|
||||
$$
|
||||
|
||||
|
||||
## 四、TD3
|
||||
|
||||
在Double DQN中，高估问题通过解耦最优动作选取与最优动作价值函数计算得到了缓解，这种思路在TD3中得到了延续。作为Actor-Critic框架下的确定性强化学习算法，TD3结合了深度确定性策略梯度算法和双重网络，在缓解DDPG算法的高估问题时取得了优秀表现。
|
||||
|
||||
### 1. 双重网络
|
||||
|
||||
不同于DDPG中Actor-Target Actor和Critic-Target Critic的四网络结构，TD3算法在DDPG的基础上新增了一套Critic_2网络。两个Target Critic网络计算出各自的Q-target后，选取 $\min(targetQ_1，targetQ_2)$ 作为原DDPG中 $Q(a')$ 的替代去计算更新目标Q-target，公式如下：
|
||||
$$
|
||||
Y_{target} = r+\gamma \min(targetQ_1, targetQ_2)
|
||||
$$
|
||||
两个Critic网络根据Actor的输出分别计算出各自的值 $Q_1,Q_2$ 后，通过 $MSE$ 计算Q值与Q-target之间的Loss，进行参数更新，公式如下：
|
||||
$$
|
||||
\theta_i = argmin_{\theta_i}\frac{1}{N}\sum(y-Q_{\theta_i}(s,a))^2
|
||||
$$
|
||||
当Critic网络更新完成后，Actor网络采用延时更新的方法，通过梯度上升自我更新。target网络则是采用软更新的方式进行更新，二者更新公式如下：
|
||||
$$
|
||||
Actor:\ \nabla_{\phi}J(\phi)=\frac{1}{N} \sum\nabla_aQ_{\theta_1}(s,a)|a=\pi_{\phi}(s)\nabla_{\phi}\pi_{\phi}(s) \\
|
||||
target:\ \theta=\tau\theta'+(1-\tau)\theta
|
||||
$$
|
||||
|
||||
|
||||
### 2. 目标策略平滑正则化
|
||||
|
||||
DDPG中采用的确定性策略会在更新Critic网络时极易被函数逼近误差所影响，致使目标估计的方差值增大，估值异常。TD3中引入了平滑化思想（Smoothing），通过向目标动作中添加正态分布噪声并求平均值来近似动作期望，本质是一种正则化方法，采用噪声来平滑掉Q峰值，从而防止其过拟合。公式表示为：
|
||||
$$
|
||||
a'=\pi_{\phi'}(s')+\epsilon, \\ \epsilon \sim clip(N(0, \tilde \sigma), -c,c)
|
||||
$$
|
||||
|
||||
|
||||
### 3. 延迟更新
|
||||
|
||||
在训练Actor和Critic网络时，文章发现Actor与Critic之间的相互作用会导致Actor一直在被动的跟随Critic网络进行更新，这种不稳定的状态会使得策略函数会根据不准确的估值朝着错误方向进行更新，并在多次更新中累积这些差异，最终陷入劣化循环。因此Actor网络需要一个稳定的Critic网络来协助其进行更新。
|
||||
|
||||
文章调高了Critic网络的更新频率，使其高于Actor。保证先尽可能的降低估计误差，确保TD-error足够小。待获得更加稳定的结果后再去协助Actor网络进行更新。
|
||||
|
||||
|
||||
|
||||
## 五、实验环节
|
||||
|
||||
### 1. 评估
|
||||
|
||||
本文采用MuJoCo连续控制任务对TD3与PPO、DDPG及其他算法进行评估，其中DDPG模型通过一个两层的前馈神经网络实现，并在每层之间对Actor和Critic均采用了ReLU和Tanh单元，同时作者还针对原始DDPG算法进行了修改，将状态和动作共同接受并输入第一层中。两个网络参数都采用Adam进行更新，设置学习率为$10^{-3}$。
|
||||
|
||||
目标策略平滑通过添加 $\epsilon \sim N(0, 0.2)$ 实现，将其剪辑到区间$(-0.5,0.5)$。延迟更新策略设置每2次迭代更新Actor与Target Critic。在进行软更新时，设置 $\tau=0.005$。
|
||||
|
||||
在HalfCheetah-v1、Hopper-v1等环境中学习曲线越靠上，算法效果越好。具体结果如下图所示：
|
||||
|
||||
|
||||
|
||||
可见TD3算法的性能相较于其他算法有较明显提升。
|
||||
|
||||
|
||||
|
||||
### 2. 消融实验
|
||||
|
||||
本节作者针对延迟更新策略DP、目标策略平滑TPS及双Q值学习梯度截取CDQ三个策略进行了消融实验；此外作者还对Double Q-learning和Double DQN中Actor-Critic结构的有效性进行了讨论，具体结果如下：
|
||||
|
||||
<img src="img\TD_2.png" style="zoom:150%;" />
|
||||
|
||||
可以看到DP和TPS策略的消融实验对结果影响略小，CDQ结构去掉后结果存在明显变化，证明抑制无偏估计量的高估对于提升算法性能具有显著提高作用。
|
||||
|
||||
|
||||
|
||||
## 六、文章贡献
|
||||
|
||||
在本文中，贡献主要包括如下几点：
|
||||
|
||||
1. 设置类似Double DQN的网络，通过两套Critic网络进行Q值估算，解决了DDPG中存在的Q值高估问题，并通过消融实验证明其重要性。
|
||||
2. 针对Actor与Critic网络相互作用导致Actor不稳定的问题，通过设置Actor延迟更新进行解决。
|
||||
3. 通过添加平滑噪声的方式优化方差计算时的峰值，解决由于估值函数对真实值拟合不精确带来的方差问题。
|
||||
|
||||
|
||||
========
|
||||
|
||||
作者：王振凯
|
||||
|
||||
研究方向：深度学习、强化学习
|
||||
|
||||
河北地质大学研究生在读
|
||||
|
||||
|
||||
|
||||
|
||||
@@ -0,0 +1,46 @@
|
||||
## Asynchronous Methods for Deep Reinforcement Learning
|
||||
|
||||
[论文地址](https://arxiv.org/abs/1602.01783)
|
||||
|
||||
本文贡献在于提出一种异步梯度优化框架，在各类型rl算法上都有较好效果，其中效果最好的就是（asynchronous advantage actor-critic, A3C）。
|
||||
|
||||
- **Motivation(Why)**:基于经验回放的drl算法在一些任务上效果较差，可以采用其他的方式来使用数据训练网络
|
||||
- **Main Idea(What)**:使用异步并行的方式让多个agent与环境进行交互，当某一个agent交互完计算梯度后就交给global进行更新，更新完再同步给这个agent，其他agent做同样的操作。
|
||||
|
||||
这里给张李宏毅老师的讲解图：
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
框架思想较为简单，但优点很多：
|
||||
|
||||
1. 适用范围广，on/off policy、离散/连续型任务均可使用
|
||||
|
||||
2. 多个agent采样数据减少数据相关性，训练更稳定
|
||||
|
||||
3. 不需要经验回放，让框架不局限于off-policy，同时减少内存算力消耗
|
||||
|
||||
4. 相较分布式所需资源更少，不用gpu，使用一台多核cpu机器时间更短
|
||||
|
||||
|
||||
|
||||
本文使用hogwild! 方法来更新梯度，不清楚的可参考[知乎讲解](https://zhuanlan.zhihu.com/p/30826161)，下图来源此文：
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
这里举个栗子：假设网络有100个参数，worker i传来的梯度更新了40个参数后worker j就开始更新了，当$i$更新完后前面的一些参数被j更新了（被覆盖掉了），但不要紧，i更新完了照样把当前global参数同步给i，这就是Asynchronous的意思。
|
||||
|
||||
A3C：
|
||||
|
||||
|
||||
|
||||
实验结果:
|
||||
|
||||
|
||||
@@ -0,0 +1,144 @@
|
||||
# Deterministic Policy Gradient Algorithms（DPG）
|
||||
作者：David Silver，Guy Lever，Nicolas Heess, Thomas Degris, Daan Wierstra, Martin Riedmiller <br>
|
||||
单位：DeepMind Technologies, London, UK；University College London, UK <br>
|
||||
论文发表会议：Proceedings of the 31st International Conference on Machine Learning <br>
|
||||
论文发表时间：2014 <br>
|
||||
论文地址：https://www.deepmind.com/publications/deterministic-policy-gradient-algorithms <br>
|
||||
|
||||
论文贡献：这篇论文提出了确定性的策略梯度算法，是对之前的随机性梯度策略算法的发展。
|
||||
|
||||
# 一、研究动机
|
||||
在随机策略梯度算法之中，计算其目标函数梯度的期望需要在状态空间和动作空间进行积分，也就是说采样时需要尽可能地覆盖到所有的状态空间和动作空间，所以就需要尽可能多地采样。但是如果策略是一个确定性的策略，那么积分就只需要在状态空间上进行，这样就大大减小了需要采样的数目。
|
||||
|
||||
# 二、随机策略梯度算法
|
||||
### 一个基本的setting：<br>
|
||||
整个过程被定义为一个马尔可夫决策过程（Markov decision process），一个轨迹（状态、动作、奖励）具体如下所示：
|
||||
$$
|
||||
s_{1}, a_{1}, r_{1}..., s_{T}, a_{T}, r_{T}
|
||||
$$
|
||||
<br>
|
||||
|
||||
### 一些基本的符号定义:
|
||||
|
||||
随机性策略：$\pi_{\theta}(s)$
|
||||
状态价值函数: $V^{\pi}(s)$
|
||||
动作价值函数：$Q^{\pi}(s,a)$
|
||||
|
||||
### 随机策略梯度理论（Stochastic Policy Gradient Theorem）
|
||||
|
||||
策略的表现目标函数（performance objective）：
|
||||
$$ J(\pi_{\theta})=\int_{S}^{}\rho^{\pi}(s)\int_{A}^{}\pi_{\theta}(s,a)r(s,a) dads $$
|
||||
该目标函数的梯度：
|
||||
$$ \nabla_{\theta}J(\pi_{\theta})=\int_{S}^{}\rho^{\pi}(s)\int_{S}^{}\nabla_{\theta}\pi_{\theta}(a|s)Q^{\pi}(s,a)dads $$
|
||||
$$ =E_{s\sim\rho^{\pi},a\sim\pi_{\theta}}[\nabla_{\theta}\pi_{\theta}(a|s)Q^{\pi}(s,a)] $$
|
||||
理论内容：把策略参数 $\theta$ 向策略梯度的方向调整，以实现最大化目标函数。但是在实际实现的过程中，这里的期望是通过采样轨迹来实现的。同时还要关注的一个问题是这里的动作价值函数$Q^{\pi}(s,a)$要如何得到。一个思路是直接用采样中的实际累计奖励$r^{\gamma}_{t}$来估计$Q^{\pi}(s_{t},a_{t})$,这也就是REINFORCE算法。
|
||||
|
||||
### 随机演员-评论员算法（Stochastic Actor-Critic Algorithms）
|
||||
|
||||
算法内容：我们称动作价值函数拟合器$Q^{w}(s,a)$为评论员（Critic），策略$\pi_{\theta}$为演员（Actor），通过交替更新评论员和演员来实现最大化目标函数。更新的过程可以理解为$Q^{w}(s,a)$逐步拟合真实的动作价值函数$Q^{\pi}(s,a)$，策略$\pi_{\theta}$根据$Q^{w}(s,a)$不断地优化参数$\theta$。
|
||||
|
||||
注：在这个过程中会有这样一个问题：我们引入了$Q^{w}(s,a)$来估计真实的$Q^{\pi}(s,a)$，在这个过程中有可能会存在偏差。所以，文中给出两个条件，只要$Q^{w}(s,a)$满足这两个条件，那么就不会引入偏差。这两个条件为（这部分不是很重要，可跳过）：
|
||||
1) $$ \quad Q^{w}(s,a)=\nabla_{\theta}log\pi_{\theta}(a|s)^{T}w$$
|
||||
|
||||
2) $\quad$ $Q^{w}(s,a)$的参数w需要满足最小化下面这个均方误差（MSE）：
|
||||
$$ \quad \epsilon^{2}(w)=E_{s\sim\rho^{\pi},a\sim\pi_{\theta}}[(Q^{w}(s,a)-Q^{\pi}(s,a))^{2}]$$
|
||||
|
||||
### 异策略演员-评论员算法（Off-Policy Actor-Critic）
|
||||
该算法和原始的演员-评论员算法的区别在于用于采样轨迹的策略（behaviour policy: $\beta(a|s)$）和实际更新的策略（target policy: $\pi_{\theta}(a|s)$）不一致，即
|
||||
$$ \beta(a|s)\neq\pi_{\theta}(a|s) $$
|
||||
在原始的演员-评论员算法中，每次采样来计算目标函数的时候，由于策略已经进行了更新，都需要重新采样，这样的话采样得到的轨迹的利用率就很低。所以考虑采样和实际更新的策略采用不同的策略，这样就可以提高采样的利用率。具体推导如下：
|
||||
该算法中的目标函数：
|
||||
$$ J_{\beta}(\pi_{\theta})=\int_{S}^{}\rho^{\beta}(s)V^{\pi}(s)ds$$
|
||||
$$ \quad\quad =\int_{S}\int_{A}\rho^{\beta}(s)\pi_{\theta}(a|s)Q^{\pi}(s,a)dads$$
|
||||
该算法中的目标函数的梯度：
|
||||
$$ \nabla_{\theta}J_{\beta}(\pi_{\theta})\approx\int_{S}\int_{A}\rho^{\beta}(s)\nabla_{\theta}\pi_{\theta}(a|s)Q^{\pi}(s,a)dads$$
|
||||
$$ =\int_{S}\int_{A}\rho^{\beta}(s)\pi_{\theta}(a|s)\nabla_{\theta}log\pi_{\theta}(a|s)Q^{\pi}(s,a)dads$$
|
||||
$$ =\int_{S}\int_{A}\rho^{\beta}(s)\beta(a|s)\frac{\pi_{\theta}(a|s)}{\beta(a|s)}\nabla_{\theta}log\pi_{\theta}(a|s)Q^{\pi}(a|s)dads$$
|
||||
$$ =E_{s\sim\rho^{\beta},a\sim\beta}[\frac{\pi_{\theta}(a|s)}{\beta(a|s)}\nabla_{\theta}log\pi_{\theta}(a|s)Q^{\pi}(a|s)]$$
|
||||
在更新策略参数的时候，我们就用采样得到的轨迹目标函数梯度的平均（对期望的估计）更新策略的参数。这个采样过程也称为重要性采样。
|
||||
|
||||
# 三、确定性策略梯度算法（Deterministic Policy Gradient Algorithms）
|
||||
确定性策略梯度算法和随机策略梯度算法最大的不同就是策略的形式（一个是带有随机性，一个是确定的），除此自外这两者的发展思路都差不多。
|
||||
### 一些基本的符号定义：
|
||||
确定性策略：$\mu_{\theta}(s)$
|
||||
状态价值函数: $V^{\mu}(s)$
|
||||
动作价值函数：$Q^{\mu}(s,a)=Q^{\mu}(s,\mu_{\theta}(s))$
|
||||
|
||||
### 确定性策略梯度理论（Deterministic Policy Gradient Theorem）
|
||||
目标函数（performance objective）：
|
||||
$$ J(\mu_{\theta})=\int_{S}\rho^{\mu}(s)r(s,\mu_{\theta}(s))ds$$
|
||||
$$ =E_{s\sim\rho^{\mu}}[r(s,\mu_{\theta}(s))]$$
|
||||
目标函数的梯度：
|
||||
$$ \nabla_{\theta}J(\mu_{\theta})=\int_{S}\rho^{\mu}(s)\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu}(s,a)|_{a=\mu_{\theta}(s)}ds$$
|
||||
$$ =E_{s\sim\rho^{\mu}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu}(s,a)|_{a=\mu_{\theta}(s)}]$$
|
||||
理论内容：
|
||||
这个和随机策略梯度理论基本上一样，就是将策略的参数向目标函数的梯度方向调整，以最大化目标函数。参数更新的数学形式的表达即为：
|
||||
$$ \theta_{k+1}=\theta_{k}+\alpha E_{s\sim\rho^{\mu_{k}}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu_{k}}(s,a)|_{a=\mu_{\theta}(s)}]$$
|
||||
注意到，这里的目标函数也是期望的形式，但是和随机策略梯度算法中的目标函数不同之处在于，这里的期望是只对状态空间进行积分，而随机策略梯度算法中的目标函数是对状态空间以及动作空间进行积分。这也就意味着在通过采样估计目标函数的时候，确定性策略梯度算法需要的采样数更少。在论文中作者还证明了确定性策略梯度理论是随机策略梯度理论的一种极限情况，这一点就不列在这里了，有需要的可以去看原论文。
|
||||
|
||||
### 确定性演员-评论员算法（Deterministic Actor-Critic Algorithms）
|
||||
（这里最核心的是关注$\theta$是如何更新的）
|
||||
#### 同策略演员-评论员算法（On-Policy Deterministic Actor-Critic）
|
||||
一般来说，确定性的策略在采样的时候很难有多样性，除非是在环境噪声很大的情况下。这里介绍同策略演员-评论员算法只是为了更好地理解确定性演员-评论员算法。
|
||||
该算法分为两步：更新动作价值函数拟合器$Q^{w}(s,a)$的参数，使其更好地拟合真实的动作价值函数$Q^{\mu}(s,a)$；更新确定性策略$\mu_{\theta}(s)$的参数$\theta$，进行梯度上升。
|
||||
数学形式如下：
|
||||
$$ \delta_{t}=r_{t}+\gamma Q^{w}(s_{t+1},a_{t+1})-Q^{w}(s_{t},a_{t})$$
|
||||
$$ w_{t+1}=w_{t}+\alpha_{\theta}\delta_{t}\nabla_{w}Q^{w}(s_{t},a_{t})$$
|
||||
$$ \theta_{t+1}=\theta_{t}+\alpha_{\theta}\nabla_{\theta}\mu_{\theta}(s_{t})\nabla_{a}Q^{\mu_{k}}(s_{t},a_{t})|_{a=\mu_{\theta}(s)}$$
|
||||
#### 异策略演员-评论员算法（Off-Policy Deterministic Actor-Critic）
|
||||
在确定性策略梯度算法中应用异策略演员-评论员算法的原因不同于随机策略梯度算法，这里是为了使得采样得到的轨迹更加具有多样性。这里直接给出异策略演员-评论员算法中的目标函数以及目标函数梯度的形式：
|
||||
$$ J_{\beta}(\mu_{\theta})=\int_{S}\rho^{\beta}(s)V^{\mu}(s)ds$$
|
||||
$$ \nabla_{\theta}J_{\beta}(\mu_{\theta})\approx\int_{S}\rho^{\beta}(s)\nabla_{\theta}\mu_{\theta}(a|s)Q^{\mu}(s,a)ds$$
|
||||
$$ =E_{s\sim\rho^{\beta}}[\nabla_{\theta}\mu_{\theta}(s)\nabla_{a}Q^{\mu_{k}}(s,a)|_{a=\mu_{\theta}(s)}]$$
|
||||
算法更新的数学形式为：
|
||||
$$ \delta_{t}=r_{t}+\gamma Q^{w}(s_{t+1},a_{t+1})-Q^{w}(s_{t},a_{t})$$
|
||||
$$ w_{t+1}=w_{t}+\alpha_{\theta}\delta_{t}\nabla_{w}Q^{w}(s_{t},a_{t})$$
|
||||
$$ \theta_{t+1}=\theta_{t}+\alpha_{\theta}\nabla_{\theta}\mu_{\theta}(s_{t})\nabla_{a}Q^{\mu_{k}}(s_{t},a_{t})|_{a=\mu_{\theta}(s)}$$
|
||||
注意到，这里的算法更新的形式和同策略演员-评论员算法是完全一样的，这是因为我们更新参数的时候并没有用到策略梯度的期望，而是用单个采样轨迹的目标函数的梯度进行更新的，所以同策略和异策略算法在表现形式上完全一样，不同之处在于用于更新的采样轨迹，异策略算法中的采样轨迹更具有多样性。但是我们在实际应用的时候，我认为还是应该用期望来更新策略参数，而不是单个样本的梯度。
|
||||
|
||||
# 四、算法总结
|
||||
这篇论文介绍的核心的算法就是确定性策略的异策略演员-评论员算法，算法的大概流程就是：
|
||||
1. 基于探索策略（$\beta(s)$），对轨迹进行采样
|
||||
2. 利用Sarsa算法或者Q-learning对$Q^{w}(s,\mu_{\theta}(s))$的参数w进行更新，使其更好地拟合$Q^{\mu}(s,\mu_{\theta}(s))$
|
||||
3. 利用梯度上升对确定性策略$\mu_{\theta}(s)$的参数$\theta$进行更新
|
||||
4. 循环这个过程
|
||||
|
||||
|
||||
注：关于如何更新$Q^{w}(s,\mu_{\theta}(s,a))$，这里不做具体介绍。在实际应用算法的时候我们需要考虑如何对$Q^{w}(s,a)$，$\mu_{\theta}(s)$进行建模，可以用特征工程+线性回归的方法进行建模，也可以考虑用神经网络对其进行建模，但是无论用哪种方式，要考虑建模的时候是否会引入偏差，原论文中对于$Q^{w}(s,a)$应该满足何种形式才不会引入偏差进行了详细的讨论，我没有在这篇文章中列出来，有需要的可以去找原论文来看。这篇文章写于2014年，那时候深度学习还没有在RL中广泛的应用，所以原论文有些内容并不是以深度学习广泛应用为大前提来写的，我们要认识到这一点。下文提到的COPDAC(compatible off-policy deterministic actorcritic)就理解为对$Q^{w}(s,a)$, $\mu_{\theta}(s)$进行了特殊的建模就好了，至于怎么建模的，其实不太重要，因为现在一般都用神经网络来建模了。
|
||||
# 五、实验
|
||||
这部分设置了三个情景来验证确定性策略梯度算法的效果。
|
||||
### 连续的老虎机（Continuous Bandit）
|
||||
#### 实验设置
|
||||
分别在动作空间维数m=10，25，50的setting下应用了stochastic actor-critic (SAC-B)、deterministic actor-critic (COPDAC-B)两种算法。老虎机可以视为一种弱化的强化学习，即一个回合只有一个时间步。这里的cost是衡量目前的策略相比于最优策略，差了多少，所以cost越低越好。
|
||||
|
||||
|
||||
#### 实验结果
|
||||
可以看出，COPDAC-B的效果远远好于SAC-B，而且动作空间的维数越大，其优势越明显。
|
||||
### 连续的强化学习（Continuous Reinforcement Learning）
|
||||
#### 实验设置
|
||||
三个游戏环境分别为：mountain car、pendulum、2D puddle world，其动作空间都是连续的。分别在这三个游戏环境中应用stochastic on-policy actor-critic (SAC)、 stochastic off-policy actor-critic (OffPAC)、deterministic off-policy actor-critic (COPDAC)三种算法。
|
||||
|
||||
|
||||
#### 实验结果
|
||||
可以看出来，COPDAC-Q在三种环境中均表现最好。而且COPDAC-Q收敛的更快，这是因为他需要的采样数更少。
|
||||
### 章鱼手控制（Octopus Arm）
|
||||
#### 实验设置
|
||||
Octopus Arm是一个具有多个自由度的机械手，这个实验的目标是这个机械手触碰到目标。实验过程中的奖励和机械手与目标之间的距离改变成正比（即离目标越近，奖励越多），当触碰到目标或者进行了300步时，一个过程结束。这里用两个感知机来建模$Q^{w}(s,a)$和$\mu_{\theta}(s)$。实验结果如下：
|
||||
|
||||
|
||||
#### 实验结果
|
||||
可以看到，算法学到了较好的策略，触碰到目标需要的步数越来越少，一个完整过程所得到的回报越来越多。
|
||||
|
||||
## 参考文献
|
||||
1. Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D. & Riedmiller, M.. (2014). Deterministic Policy Gradient Algorithms. Available from https://proceedings.mlr.press/v32/silver14.html. <br>
|
||||
2. [论文十问-快速理解论文主旨的框架](https://www.cnblogs.com/xuyaowen/p/raad-paper.html)<br>
|
||||
3. [蘑菇书EasyRL](https://github.com/datawhalechina/easy-rl)
|
||||
|
||||
|
||||
=============================<br>
|
||||
作者：赵世天 <br>
|
||||
所属院校：华东师范大学<br>
|
||||
研究方向：计算机视觉、深度学习<br>
|
||||
联系邮箱：shitian_zhao@163.com
|
||||
|
||||
关于我：华东师范大学本科在读，目前在做一些多模态和域泛化的研究，知乎重度使用者。大家一起交流学习吧。
|
||||
@@ -0,0 +1,351 @@
|
||||
## High-Dimensional Continuous Control Using Generalised Advantage Estimation
|
||||
|
||||
## 广义优势估计(GAE)：高维连续空间的控制的解决方案
|
||||
|
||||
> **John Schulman, Philipp Moritz, Sergey Levine, Michael I. Jordan and Pieter Abbeel**
|
||||
>
|
||||
> Department of Electrical Engineering and Computer Science
|
||||
>
|
||||
> University of California, Berkeley
|
||||
>
|
||||
> {joschu,pcmoritz,levine,jordan,pabbeel}@eecs.berkeley.edu
|
||||
>
|
||||
> http://arxiv.org/abs/1506.02438
|
||||
|
||||
### 1 引入与概览 / Introduction
|
||||
|
||||
* 强化学习需要解决的两个重大问题分别是**奖励分配问题（credit assignment problem）**和**远期奖励问题（distal reward problem）**，我们通常使用值函数可以巧妙地解决第一个问题（在DRL中直接将其交给神经网络去完成）
|
||||
* 在使用**随机梯度上升算法（stochastic gradient ascent）**时我们可以得到梯度矩阵的无偏估计（unbiased estimation），但其高方差的特性在时间角度上显得让人无法承受（因为这样带有较大噪声的估计时序上与其他估计相混合，会变成什么样子我们也不得而知）
|
||||
* 相比于经验回报（Empirical Return），**演员-评论员（Actor-Critic）算法**以偏差（bias）为代价采用神经网络来估计值函数
|
||||
* 作者认为，高数据量会导致模型过拟合（高方差），但更严重的是引起的偏差无法用数据量解决——这可能导致模型发散或收敛到局部极小值
|
||||
* **作者提供了一族策略梯度估计函数$\text{GAE}(\gamma, \lambda),~ \gamma, \lambda \in [0,1]$，在引入可承受的偏差同时极大降低方差**
|
||||
* **作者使用GAE在高难度的3D控制环境中进行训练**
|
||||
|
||||
### 2 预备 / Preliminaries
|
||||
|
||||
#### 2.1 估计策略梯度
|
||||
|
||||
已知从某分布$\rho_0$采样的初始状态$s_0$，按照策略$\pi(a|s)$和状态转换分布函数$P(s'|s, a)$生成一条轨迹（trajectory）。在每个时间节点（time step）时智能体收到一个奖励$r_t = r(s_t, a_t, s_{t+1})$。因为我们需要将期望回报最大化，因此我们对期望回报$\mathbb E\left[\displaystyle \sum_{t=0}^\infty r_t \right]$求梯度：
|
||||
$$
|
||||
g := \nabla_\theta \mathbb E\left[ \sum_{t=0}^\infty r_t \right] = \mathbb E\left[ \sum_{t = 0}^\infty \Psi_t\nabla_\theta \log \pi_\theta(a_t|s_t) \right]
|
||||
$$
|
||||
|
||||
> 对于上述等式的详细推导过程，在此给出一个不严谨但方便理解的版本，以值函数对参数求偏导为例：
|
||||
> $$
|
||||
> \begin{align}
|
||||
> \frac{\part V(s;\boldsymbol \theta)}{\part \boldsymbol \theta} &=
|
||||
> \frac{\part \sum_a \pi(a|s; \boldsymbol \theta)\cdot Q_\pi(s, a)}{\part \boldsymbol \theta}
|
||||
> \\
|
||||
> &= \sum_a\frac{\part \pi(a|s; \boldsymbol \theta)\cdot Q_\pi(s, a)}{\part \boldsymbol \theta}
|
||||
> \\
|
||||
> &= \sum_a\frac{\part \pi(a|s; \boldsymbol \theta)}{\part \boldsymbol \theta}\cdot Q_\pi(s, a) & \text{assume } Q_\pi \text{is independent of }\boldsymbol \theta
|
||||
> \\
|
||||
> &= \sum_a\pi(a|s; \boldsymbol \theta) \cdot \frac{\part \log \pi(a|s; \boldsymbol \theta)}{\part \boldsymbol \theta}\cdot Q_\pi(s, a) &\text{chain rule}
|
||||
> \\
|
||||
> &= \mathbb E_A\left[\frac{\part \log \pi(A|s; \boldsymbol \theta)}{\part \boldsymbol \theta}\cdot Q_\pi(s, A)\right]
|
||||
> \end{align}
|
||||
> $$
|
||||
> Remark. 证明参考自[Shusen Wang, Deep Reinforcement Learning](https://www.bilibili.com/video/BV1rv41167yx/?is_story_h5=false&p=1&share_from=ugc&share_medium=android&share_plat=android&share_session_id=9b64fa10-a83a-4a62-8104-4b8bb316ebdb&share_source=WEIXIN&share_tag=s_i×tamp=1667564212&unique_k=TKDw0q7&vd_source=81247b204d5fa64ef8de53fe75ccd121)
|
||||
|
||||
式中的$\Psi_t$可以被下面的这些表达式替换:
|
||||
|
||||
* $\displaystyle \sum_{t=0}^\infty r_t$：奖励总和
|
||||
* $\displaystyle \sum_{t'=t}^\infty r_{t'}$：某时刻后的奖励总和
|
||||
* $\displaystyle \sum_{t'=t}^\infty r_{t'} - b(s_t)$：减去了基准（baseline）的某时刻后奖励总和
|
||||
* $Q^\pi(s_t, a_t)$：Q函数
|
||||
* $\displaystyle A^\pi (s_t, a_t) := Q^\pi(s_t, a_t) - V^\pi(s_t)$：**优势函数（advantage function）**
|
||||
* $r_t + V^\pi(s_{t+1})- V^\pi(s_t)$：TD残差（temporal difference residual）
|
||||
|
||||
|
||||
|
||||
#### 2.2 优势函数
|
||||
|
||||
仔细观察上面的几个表达式，我们会发现优势函数和第三项十分相似——如果我们将基准换成值函数，那么他只和优势函数相差一个常数。作者在文中提到在上述这么多可选项中优势函数引入的方差最低。这结合求梯度的公式不难理解。我们事先约定$V^\pi$是智能体位于某状态的未来回报的**期望**，这样优势函数就可以很好的解构成有明确意义的两部分：
|
||||
$$
|
||||
\displaystyle A^\pi (s_t, a_t) := \underbrace{Q^\pi(s_t, a_t)}_{在t时刻采用动作a_t后的期望回报} - \underbrace{V^\pi(s_t)}_{智能体还没有采取行动时的期望回报}
|
||||
$$
|
||||
我们又注意到在梯度中$A^\pi$和$\nabla_\theta \log \pi_\theta$是相乘的关系，我们就可以在训练过程中增加 “更好的” 动作被选上的概率，因为$Q$函数值低于平均值的对应的优势函数为负值，这样会让参数沿着梯度的相反方向走；同理更好的动作会让参数沿着梯度方向走，这就可以推出上面的结论。
|
||||
|
||||
|
||||
|
||||
#### 2.3 无偏的优势估计
|
||||
|
||||
我们在此基础上更进一步：引入参数$\gamma$：
|
||||
$$
|
||||
\begin{align}
|
||||
V^{\pi,\gamma}(s_t) & = \mathbb E_{s_{t+1}:\infty,a_{t}:\infty}
|
||||
\left[ \sum_{l = 0}^\infty \gamma^lr_{t + l} \right]
|
||||
\\
|
||||
Q^{\pi,\gamma}(s_t, a_t) & = \mathbb E_{s_{t+1}:\infty,a_{t+1}:\infty}
|
||||
\left[ \sum_{l = 0}^\infty \gamma^lr_{t + l} \right]
|
||||
\\
|
||||
A^{\pi, \gamma}(s_t, a_t) & = Q^{\pi,\gamma}(s_t, a_t) - V^{\pi,\gamma}(s_t)
|
||||
\end{align}
|
||||
$$
|
||||
|
||||
> Remark. 期望符号的下标意义是求期望的区间。例如，值函数的区间是从本次动作和下次状态开始直至结束，而Q函数则已知当此动作，因此它的下标是从$a_{t+1}$开始的
|
||||
|
||||
这样我们可以得到策略梯度$g$的一个估计：
|
||||
$$
|
||||
g^\gamma
|
||||
:= \mathbb E_{s_{0}:\infty,a_{0}:\infty} \left[ \sum_{t = 0}^\infty A^{\pi, \gamma}(s_t, a_t) \nabla_\theta \log \pi_\theta(a_t|s_t) \right]
|
||||
$$
|
||||
在我们往下讲之前先介绍一个概念并不加证明的引入一些命题（如果对证明有兴趣的话可以参看[原论文](http://arxiv.org/abs/1506.02438)）
|
||||
|
||||
|
||||
|
||||
**定义1 $\gamma$-无偏（$\gamma$-just）** 若$A^{\pi,\gamma}$的某个逼近$\hat A$满足对任意的$t$，都有
|
||||
$$
|
||||
\mathbb E_{s_{0}:\infty,a_{0}:\infty}
|
||||
\left[
|
||||
\sum_{t = 0}^\infty \hat A_t(s_{0:\infty}, a_{0:\infty})
|
||||
\nabla_\theta \log \pi_\theta(a_t|s_t)
|
||||
\right]
|
||||
=
|
||||
\mathbb E_{s_{0}:\infty,a_{0}:\infty} \left[ \sum_{t = 0}^\infty A^{\pi, \gamma}(s_t, a_t) \nabla_\theta \log \pi_\theta(a_t|s_t) \right]
|
||||
$$
|
||||
我们称$\hat A$是$\gamma$-无偏的。显然满足条件的$\hat A$带入上式，其值总是等于$g^\gamma$.
|
||||
|
||||
|
||||
|
||||
**命题1** 若不论我们取怎样的$(s_t,a_t)$，$\hat A$总是可以被写为$\hat A_t(s_{0:\infty}, a_{0:\infty}) = Q_t(s_{t:\infty}, a_{t:\infty}) - b_t(s_{0:t}, a_{0:t-1})$，且$\mathbb E_{s_{t+1}:\infty, a_{t+1}:\infty|s_t, a_t}[Q_t(s_{t:\infty}, a_{t:\infty})] = Q^{\pi,\gamma}(s_t, a_t)$，则$\hat A$是$\gamma$-无偏的.
|
||||
|
||||
|
||||
|
||||
可以验证，下面的几个式子都是$\gamma$-无偏的：
|
||||
|
||||
* $\displaystyle \sum_{l=0}^\infty \gamma^l r_{t + l}$：值函数的无偏估计
|
||||
* $Q^{\pi, \gamma}(s_t, a_t)$：令第二项为零
|
||||
* $A^{\pi,\gamma}(s_t, a_t)$：令第二项为值函数
|
||||
* $r_t + \gamma V^{\pi, \gamma}(s_{t + 1}) - V^{\pi, \gamma}(s_t)$：和上一项相同
|
||||
|
||||
|
||||
|
||||
### 3 估计优势函数 / Advantage Function Estimation
|
||||
|
||||
实际上我们不可能对梯度中的项进行求期望工作，我们在实际情况中往往选择采样平均的方式来估计策略梯度：
|
||||
$$
|
||||
\hat g = \frac 1N \sum_{n = 1}^N \sum_{t = 0}^\infty \hat A_t^n \nabla_\theta \log \pi_\theta(a_t^n|s_t^n)
|
||||
$$
|
||||
注意到$\mathbb E_{s_{t+1}}[\delta_t^{V^{\pi, \gamma}}] = A^{\pi, \gamma}(s_t, a_t)$，我们构造这样的和：
|
||||
$$
|
||||
\hat A_t^{(k)} := \sum_{l=0}^{k - 1} \gamma^l \delta_{t + l}^V = -V(s_t) + \sum_{l = 0}^{k - 1} \gamma^l r_{t + l} + \gamma^k V(s_{t + k})
|
||||
$$
|
||||
在此基础上我们可以定义**广义优势估计（generalised advantage estimation）**
|
||||
$$
|
||||
\begin{align}
|
||||
\hat A^{\text{GAE}(\gamma, \lambda)}_t :=& (1 - \lambda)\left( \hat A^{(1)}_1 + \lambda\hat A^{(2)}_1 + \lambda^2\hat A^{(3)}_1 + \cdots \right)\\
|
||||
=& (1 - \lambda) (\delta^V_t + \lambda(\delta^V_t + \gamma\delta^V_{t + 1}) + \lambda^2(\delta^V_t + \gamma\delta^V_{t + 1}+ \gamma ^ 2\delta_{t + 2}^V) + \cdots)\\
|
||||
=& (1 - \lambda)(\delta_t^V(1 + \lambda + \lambda^2 +\cdots) + \delta_{t+1}^V(\lambda + \lambda^2 + \lambda^3+\cdots) +\cdots)\\
|
||||
=& \sum_{l=0}^\infty (\gamma\lambda)^l \delta_{t + l}^V
|
||||
\end{align}
|
||||
$$
|
||||
我们考虑GAE的两种极端情况：
|
||||
$$
|
||||
\begin{align}
|
||||
\hat A^{\text{GAE}(\gamma, 0)}_t &= \delta_t &= r_t + V(s_{t+1})- V(s_t) \\
|
||||
\hat A^{\text{GAE}(\gamma, 1)}_t &= \sum_{l=0}^{\infty} \gamma^l \delta_{t + l}^V &=-V(s_t) + \sum_{l = 0}^{\infty} \gamma^l r_{t + l}~\,
|
||||
\end{align}
|
||||
$$
|
||||
若$\lambda = 0$，如果我们忽略$V$的估计误差，那么它虽然是$\gamma$-无偏的，但引入了高方差；$\lambda = 1$时方差相较于上一种情况更小，但当且仅当$V =V^{\pi, \gamma}$时才是$\gamma$无偏的，否则将会引入偏差。作者提出的GAE目的在于在两个极端之间找到一个平衡点（makes a compromise）。
|
||||
|
||||
再次观察上面的推导，我们不难发现
|
||||
|
||||
1. $\gamma$主要决定值函数$V$的缩放大小（scale），如果$\gamma < 1$则引入偏差（这个不难理解）
|
||||
2. $\lambda < 1$且估计的$V$不准时会引入偏差
|
||||
|
||||
作者研究发现，**$\lambda$的最佳值比$\gamma$的最佳值要小很多，他们认为这是$\lambda$即使在$V$不准时引入的偏差要比$\gamma$小很多导致的。**基于上面的分析我们可以使用GAE给策略梯度做一个更好的估计：
|
||||
$$
|
||||
g^\gamma \approx \mathbb E \left[
|
||||
\sum_{t = 0}^\infty \nabla_\theta \log \pi_\theta(a_t|s_t) \hat A_t^{\text{GAE}(\gamma, \lambda)}
|
||||
\right] =
|
||||
\mathbb E \left[
|
||||
\sum_{t = 0}^\infty \nabla_\theta \log \pi_\theta(a_t|s_t) \sum_{l=0}^\infty (\gamma\lambda)^l \delta_{t + l}^V
|
||||
\right]
|
||||
$$
|
||||
其中第一个约等号去等当且仅当$\lambda = 1$
|
||||
|
||||
|
||||
|
||||
### 4 通过奖励函数设计解释GAE / Interpretations as Reward Shaping
|
||||
|
||||
|
||||
|
||||
**定义2 变换的奖励函数** 已知一个从状态空间$\mathcal S$到$\mathbb R$的任意标量函数$\Phi: \mathcal S \rightarrow \mathbb R$，以及奖励函数$r(s, a ,s')$，定义变换后的奖励函数$\tilde r$：
|
||||
$$
|
||||
\tilde r(s, a, s') := r(s, a, s') + \gamma \Phi(s') - \Phi(s)
|
||||
$$
|
||||
考虑带指数衰减的变换奖励函数序列和，我们发现它与奖励函数序列和仅差一个$\Phi$
|
||||
$$
|
||||
\sum_{l = 0}^\infty \gamma^l \tilde r(s_{t+l}, a_t, s_{t + l + 1})
|
||||
=
|
||||
\sum_{l = 0}^\infty \gamma^l r(s_{t+l}, a_t, s_{t + l + 1}) - \Phi(s_t)
|
||||
$$
|
||||
我们可以仿照变换的奖励函数的定义来定义变换后的$V$，$Q$以及优势函数$A$:
|
||||
|
||||
* $\tilde Q^{\pi, \gamma}(s, a) = Q^{\pi, \gamma}(s, a) - \Phi(s)$
|
||||
* $\tilde V^{\pi, \gamma}(s) = V^{\pi, \gamma}(s) - \Phi(s)$ *(论文中为$V(s, a)$，笔者认为应该是$V(s)$，**<u>原因是：</u>**）
|
||||
* $\tilde A^{\pi, \gamma}(s, a) = (Q^{\pi, \gamma}(s, a) - \Phi(s)) - (V^{\pi, \gamma}(s) - \Phi(s)) = A^{\pi, \gamma}(s, a)$
|
||||
|
||||
> 作者在提出这三个函数时是按照逻辑的：
|
||||
>
|
||||
> 1. 通过指数衰减的序列和可以直接导出$\tilde Q$
|
||||
>
|
||||
> 2. 已经推导出$\tilde Q$以后根据$Q$和$V$的关系
|
||||
> $$
|
||||
> V(s) = \sum_{a \in \mathscr A} \pi(a|s)Q(s, a)
|
||||
> $$
|
||||
> 若将$\tilde V$定义为上式右边的$\tilde Q$得到的结果，可以进行下列变换
|
||||
> $$
|
||||
> \tilde V(s) = \sum_{a \in \mathscr A} \pi(a|s)\tilde Q(s, a) =\sum_{a \in \mathscr A} \pi(a|s)[Q(s, a) - \Phi(s)]' = V(s) - \Phi(s)
|
||||
> $$
|
||||
>
|
||||
> 3. 已知$\tilde V$和$\tilde Q$可以自然地推出$\tilde A$
|
||||
>
|
||||
> Remark. 吴恩达等的论文（[Ng et al, 1999](http://luthuli.cs.uiuc.edu/~daf/courses/games/AIpapers/ml99-shaping.pdf)）中提出这样的变换不会影响最终的最优策略（optimal policy）
|
||||
|
||||
如果$\Phi$恰好等于$V^{\pi,\gamma}$，那么$\tilde V^{\pi,\gamma} \equiv 0$
|
||||
|
||||
若令$\Phi = V$我们就得到了GAE：
|
||||
$$
|
||||
\sum_{l=0}^\infty (\gamma \lambda)^l \tilde r(s_{t + l}, a_t, s_{t + l + 1}) = \sum_{l= 0}^\infty (\gamma \lambda)^l \delta_{t + l}^V = \hat A_t^{\text{GAE}(\gamma, \lambda)}
|
||||
$$
|
||||
|
||||
---
|
||||
|
||||
为了更深入的了解变换中的参数$\gamma$和$\lambda$，我们引入下面的定义：
|
||||
|
||||
|
||||
|
||||
**定义3 响应函数**
|
||||
$$
|
||||
\chi (l;s_t, a_t) := \mathbb E[r_{t + l}|s_t, a_t] - \mathbb E[r_{t + l}|s_t]
|
||||
$$
|
||||
|
||||
|
||||
可以看出这和我们先前定义的优势函数十分相似。事实上，我们不难验证
|
||||
$$
|
||||
A^{\pi, \gamma}(s, a) = \sum_{l =0}^\infty \gamma^l \chi(l; s, a)
|
||||
$$
|
||||
通过上式我们得到：响应函数可以将优势函数在时序上进行解构的同时，也让我们将奖励分配问题量化：长时间的动作和与之对应的奖励关系与$l$远大于$0$时响应函数是否为零对应
|
||||
|
||||
我们将上面的表示带入策略梯度中期望函数中的那一项：
|
||||
$$
|
||||
\nabla_\theta \log \pi_\theta(a_t|s_t) \cdot A^{\pi, \gamma}(s_t, a_t) =
|
||||
\nabla_\theta \log \pi_\theta(a_t|s_t) \sum_{l=0}^\infty \gamma^l \chi(l;s_t, a_t)
|
||||
$$
|
||||
如果$\gamma < 1$，我们丢弃$\displaystyle l \gg \frac 1{1 - \gamma}$的所有项，上式的估计误差随着$l$的增加而迅速下降。也就是说那些距离现在太过遥远的未来收益无法被模型遇见（“forgotten”）
|
||||
|
||||
如果$\tilde r$中的$\Phi = V^{\pi, \gamma}$，则当$l \ne0$时，响应函数恒为零，对应模型只关心立即得到的回报的情况。我们当然更希望能找到一个$V \approx V^{\pi,\gamma}$来使得时序信息可以传递。这样我们就回到了$\hat A_t^{\text{GAE}(\gamma, \lambda)}$的定义。
|
||||
|
||||
> 我们可以将$\lambda^l \delta_{t + l}^V$看作缩放后的TD residual，以引入偏差，使得$V \ne V^{\pi,\gamma}$
|
||||
|
||||
从响应函数的角度，我们又可以理解为取了一个更小的参数$(\gamma \lambda)$，并使模型无法预见$\displaystyle l \gg \frac 1{1 - \gamma\lambda}$的情形
|
||||
|
||||
|
||||
|
||||
### 5 逼近值函数 / Value Function Estimation
|
||||
|
||||
|
||||
|
||||
作者采用Monte Carlo方法使非线性参数的值函数向真实值进行逼近，并使用信任区域算法对更新步长进行限制：
|
||||
$$
|
||||
\begin{align}
|
||||
\mathop{\text{minimize}}\limits_{\phi} ~~& \sum_{n = 1}^N \| V_\phi(s_n) - \hat V_n \|^2\\
|
||||
\text{s.t.}~~& \frac 1N \sum_{n = 1}^N \frac{\| V_\phi(s_n) - V_{\phi_{old}}(s_n) \|^2}{2\sigma ^2} \le \varepsilon
|
||||
\end{align}
|
||||
$$
|
||||
其中$\displaystyle \frac 1N\sum_{n = 1}^N \| V_{\phi_{old}}(s_n) - \hat V_n \|^2$
|
||||
|
||||
作者没有直接使用上面的方法，而是使用共轭梯度算法对上面的问题进行了近似，变成了下列所示的二次规划问题
|
||||
$$
|
||||
\begin{align}
|
||||
\mathop{\text{minimize}}\limits_{\phi} ~~& g^T (\phi - \phi_{old}) \\
|
||||
\text{s.t.}~~& \frac 1N \sum_{n = 1}^N (\phi - \phi_{old})^TH(\phi - \phi_{old}) \le \varepsilon
|
||||
\end{align}
|
||||
$$
|
||||
其中$H$为优化目标的Hessian矩阵的Gauss-Newton近似:
|
||||
$$
|
||||
\displaystyle H= \frac 1N\sum_n j_nj_n^T = \frac 1N \sum_n \nabla_\phi V_\phi(s_n) (\nabla_\phi V_\phi(s_n))^T
|
||||
$$
|
||||
|
||||
|
||||
### 6 算法与实践 / Experiments
|
||||
|
||||
|
||||
|
||||
**策略优化**
|
||||
|
||||
作者使用了TRPO来解决下列的受限制的优化问题：
|
||||
$$
|
||||
\begin{align}
|
||||
\mathop{\text{minimize}}\limits_{\phi} ~~& g^T (\phi - \phi_{old}) \\
|
||||
\text{s.t.}~~&
|
||||
\frac 1N \overline{D}_{KL}^{\theta_{old}}(\pi_{old}, \pi_{\theta}) \le \varepsilon\\
|
||||
\text{where}~~&
|
||||
L_{\theta_{old}}(\theta) = \frac 1N \sum_{n = 0}^N \frac{\pi_{\theta}(a_n|s_n)}{\pi_{\theta_{old}}(a_n|s_n)}\hat A_n\\
|
||||
& \overline{D}_{KL}^{\theta_{old}}(\pi_{old}, \pi_{\theta}) =
|
||||
\frac 1N \sum_{n = 1}^N D_{KL}[\pi_{\theta_{old}}(\cdot | s_n) \| \pi_\theta(\cdot | s_n)]
|
||||
|
||||
\end{align}
|
||||
$$
|
||||
同样地，作者也通过将优化目标线性化以及将限制条件变成二次形式来进一步处理。
|
||||
|
||||
|
||||
|
||||
**算法**
|
||||
|
||||
<img src="img/GAE_1.png" alt="image-20221108130714411" style="zoom:70%;" />
|
||||
|
||||
|
||||
|
||||
**实践**
|
||||
|
||||
作者在倒立摆、双足运动、四组运动、站立这三个3D任务上采用相同的神经网络结构进行训练。结果如下：
|
||||
|
||||
<img src="img/GAE_2.png" alt="image-20221108131755416" style="zoom:70%;" />
|
||||
|
||||
|
||||
|
||||
<img src="./img/GAE_3.png" alt="image-20221108131812962" style="zoom:70%;" />
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 7 讨论 / Discussion
|
||||
|
||||
* 策略梯度算法虽然可以将强化学习任务简化为无偏的随机梯度下降任务，但迄今为止（论文时间）其解决较为困难的控制问题的能力因其较高的采样复杂度而有所限制
|
||||
* 作者提出了使用两个参数来平衡模型的方差和偏差的方法，并采用信赖域算法使模型在较为困难的控制问题中可以达到较好的效果
|
||||
* 实验发现，$\lambda \in [0.9, 0.99]$时的效果最好，但仍然期待将来有方法可以自动调节$\lambda$的值
|
||||
* 目前策略梯度误差与值函数估计误差之间的关系尚不明确，如果我们知道它们之间的关系，就可以根据策略梯度误差函数选择合适的值函数估计误差的度量
|
||||
* 另一种可能的方法是通过相同的结构逼近策略和值函数，并使用GAE优化前者。但如何将其转化为数值优化问题及该方法的收敛性仍然有待考证。如果这种方案可行则会使得策略和值函数逼近是可以共用学习到的特征，以加快训练速度
|
||||
* 作者虽然发现一阶的回报（$\lambda = 0$）会导致过大的偏差以致较差的模型表现，但有研究表明如果进行合适的调整，模型也可以正常运行，不过这些研究局限于较低维度的状态和动作空间中。将这两类方法在同意条件下进行比较于将来的研究十分有用
|
||||
|
||||
|
||||
|
||||
### 8 思考 / Reflection
|
||||
|
||||
* 作者对$\lambda$和$\gamma$的作用做了合理的解释，但如果将其乘积看作是一个整体，这似乎与$\gamma$没有区别？
|
||||
* 进一步解释？
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
Binary file not shown.
Binary file not shown.
Binary file not shown.
Binary file not shown.
Binary file not shown.
Binary file not shown.
Binary file not shown.
BIN
papers/Policy_gradient/PDF/Trust Region Policy Optimization.pdf
Normal file
BIN
papers/Policy_gradient/PDF/Trust Region Policy Optimization.pdf
Normal file
Binary file not shown.
@@ -0,0 +1,209 @@
|
||||
## Proximal Policy Optimization Algorithms论文剖析
|
||||
|
||||
John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, Oleg Klimov from OpenAI
|
||||
|
||||
### 〇. 文章信息
|
||||
|
||||
Proximal Policy Optimization Algorithms
|
||||
|
||||
John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, Oleg Klimov from OpenAI， 2017
|
||||
|
||||
https://arxiv.org/abs/1707.06347
|
||||
|
||||
### 一. 写作动机
|
||||
|
||||
近年来，人们提出了几种不同的利用神经网络函数逼近进行强化学习的方法。主要的竞争者为基于价值的方法DQN，其次基于策略的方法“Vanilla Policy Gradient”（也就是最基础的策略梯度方法简称VPG。*Vanilla是个有趣的词汇，本意为香草，因为是冰淇淋最基本的口味，所以一般用其代表‘最基本’的意思，学到了*），最后是信任区域/自然策略梯度方法（TRPO）。然而这三种方法存在严重的缺点：
|
||||
|
||||
1. Deep Q-Learning在解决一些**连续动作空间**的问题上表现不佳
|
||||
2. VPG算法需要先根据当前策略函数采样一批次样本，使用样本更新后，该批次样本失效，需要重新采样，所以采样效率低下
|
||||
3. TRPO设计复杂，不兼容参数共享，dropout等结构
|
||||
|
||||
本文的写作动机就是使用一种使用一阶优化的方法就获得了复杂TRPO的良好的性能（数据采样效率，鲁棒性）。
|
||||
|
||||
### 二. 背景知识简单介绍
|
||||
|
||||
#### 1. 策略梯度算法
|
||||
|
||||
策略梯度算法将策略 $\pi$ 参数化拟合成 $\pi _\theta$ ,再通过梯度上升的方法优化参数，最常用的策略梯度有这样的形式：
|
||||
|
||||
$$ \hat{g}=\hat{\mathbb{E}_t}[\nabla _{\theta}log \pi_\theta(a_t|s_t)\hat{A_t}] \tag{1} $$
|
||||
|
||||
其中，$\hat{A_t}$为优势函数（Advantage Function）的估计量，$\mathbb{E}_t$为有限batch的平均量。可以反过来求得Loss-function：
|
||||
|
||||
$$ L(\theta)=\hat{\mathbb{E}}_t[\pi_\theta(a_t|s_t)\hat{A_t}](这里可能和原文不同，但是由于log函数单调性，其实实质是一样的) \tag{2} $$
|
||||
|
||||
工作的过程就是重复采样与模型优化。作者在这里说道：***听起来使用同一次采样的数据来多次更新策略的参数听起来十分诱人，但是后续实验证明了这样造成的影响是破坏性的***，这里的原因在下一部分会提及到。
|
||||
|
||||
#### 2. 重要性采样
|
||||
|
||||
##### （1）为什么要使用重要性采样？
|
||||
|
||||
首先回答上一部分提出的问题：**为什么同一次采样的数据无法直接用来多次更新？**
|
||||
|
||||
视线退回到策略梯度的推导。按照最初始的想法，我们想要最大化的是每一条完整的交互序列$\tau :(s_1,a_1,r_1,s_2,a_2,r_2...,s_n,a_n,r_n)$的累计奖励期望$\bar{R_\theta}(\tau)=p_\theta(\tau)R(\tau)$,通过计算策略梯度的形式通过梯度上升优化方法来更新参数，其中策略梯度为：
|
||||
|
||||
$\nabla \bar{R}_\theta=\mathbb{E}_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla log(p_\theta(\tau))] \tag{3} $
|
||||
|
||||
将其改写为针对动作-状态对的策略梯度,并使用优势函数：
|
||||
|
||||
$$\nabla \bar{R}_\theta=\mathbb{E}_{(s_t,a_t)\sim \pi_{\theta}}[\hat{A}_t\nabla log\pi_{\theta}(a_t|s_t)] \tag{4.1} $$
|
||||
|
||||
$$L(\theta)=\mathbb{E}_{(s_t,a_t)\sim \pi_{\theta}}[\pi_{\theta}(a_t|s_t)\hat{A}_t ] \tag{4.2} $$
|
||||
|
||||
具体推导可以参考我的知乎[*强化学习笔记 -6 基于策略的方法：策略梯度算法（PG)与REINFORCE - 于天琪的文章*](https://zhuanlan.zhihu.com/p/549583458 )。
|
||||
|
||||
正因公式$(4)$中，对于期望的定义（下标）要求**用来更新的的样本$(s_t, a_t)$需要是根据当前的参数化策略$\pi_\theta$来生成的**，也就意味着我们每当使用本策略采样样本进行策略参数更新后，策略已经发生了改变，所以需要重新采样改变后策略的样本。将完整序列延伸到状态-动作对也一样适用。
|
||||
|
||||
所以想要重复使用之前采样的数据多次更新策略，就需要使用一定的方法改变就样本的分布，使之与新策略产生的样本同分布，这个方法就是重要性采样。
|
||||
|
||||
##### （2）什么是重要性采样
|
||||
|
||||
当前有分布$p(x)$与$q(x)$,从$p(x)$中随机抽取样本计算函数$f(x)$的期望:$$\mathbb{E}_{x \sim p}[f(x)]=\int f(x)p(x)dx$$,若将其乘以**一个重要性因子$\frac{q(x)}{p(x)}$**,就可以使用分布$p(x)$中的采样来计算$q(x)$分布下$f(x)$的期望，即：
|
||||
|
||||
$$\mathbb{E}_{x \sim p}[\frac{q(x)}{p(x)}f(x)]=\int \frac{q(x)}{p(x)}f(x)p(x)dx=\int f(x)q(x)dx=\mathbb{E}_{x \sim q}[f(x)] \tag{5}$$
|
||||
|
||||
上述即重要性采样。将欲求期望的函数乘以一重要性因子（目标分布与采样分布之间的比值），即可从一分布中采样数据来计算另一分布的期望等。利用重要性采样，就可以改写原有的策略梯度:
|
||||
|
||||
$$\nabla \bar{R}_\theta=\mathbb{E}_{(s_t,a_t)\sim \pi_{\theta '}}[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta '}(a_t|s_t)}\hat{A}_t\nabla log\pi_{\theta}(a_t|s_t)] \tag{6.1} $$
|
||||
|
||||
$$L(\theta)=\mathbb{E}_{(s_t,a_t)\sim \pi_{\theta '}}[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta '}(a_t|s_t)}\hat{A}_t ] \tag{6.2} $$
|
||||
|
||||
##### （3）重要性采样的特殊性质
|
||||
|
||||
经过重要性采样之后，可以从$p(x)$采样求得$f(x)$在$q(x)$分布下的期望，如公式$(5)$，那么是否一劳永逸？。如果计算二者的方差就会发现：
|
||||
|
||||
$$Var_{x \sim q}[f(X)]=\mathbb{E}_{x \sim q}[f(x)^2]-[\mathbb{E}_{x \sim q}[f(x)]^2 \tag{7.1} $$
|
||||
|
||||
$$Var_{x\sim p}[\frac{q(x)}{p(x)}f(x)]=\mathbb{E}_{x \sim p}[(\frac{q(x)}{p(x)}f(x))^2]-[\mathbb{E}_{x \sim p}[\frac{q(x)}{p(x)}f(x)]^2=\mathbb{E}_{x \sim q}[f(x)^2\frac{q(x)}{p(x)}]-(\mathbb{E}_{x \sim q}[f(x)])^2 \tag{7.2 }$$
|
||||
|
||||
二者方差并不相等，其差距在重要性权重上。如果重要性权重过大，则会导致较大的方差，进一步导致采样还是失败的。
|
||||
|
||||
> 举一个来自蘑菇书《Easy RL》中的例子：
|
||||
>
|
||||
> 
|
||||
>
|
||||
> 这里的红线表示f(x)的曲线，蓝，绿线表示不同分布的x，其中纵坐标越高，在该分布中越容易被取到。其中p(x)的样本分布中，计算f(x)期望为负。实际上在利用重要性采样，从q中采样数据估计p时，有极高的几率从q(x)分布采样到的x计算f(x)为正，极少采样到x计算f(x)为负。虽然在取得为负的点计算期望时会乘以一个特别大的重要性权重使得重要性采样得到f(x)期望正确，但是前提是能采样到这样的点。在现实采样中，很有可能因为采样次数不足导致无法采样到这样的点，导致最终重要性采样失败。
|
||||
|
||||
所以，进行重要性采样的前提就是重要性权重不能过大，也就是**两个分布之间的差距不能过大**。这里我们使用KL散度评判两个分布的相似性。
|
||||
|
||||
##### （4）其他想说的
|
||||
|
||||
在面试启元RL算法岗实习生的时候，问过这样一个问题：**为什么Q-Learning之流使用Reply buffer不需要重要性采样呢？**当时我没答上来。
|
||||
|
||||
南大lamda俞扬老师的回答很容易理解。[为什么DQN不需要off policy correction? - 俞扬的回答 - 知乎](https://www.zhihu.com/question/394866647/answer/1264965104)
|
||||
|
||||
#### 3. KL散度
|
||||
|
||||
KL 散度,又可称为相对熵，是一个用来衡量两个概率分布的相似性的一个度量指标。
|
||||
|
||||
$\begin{equation*}
|
||||
\begin{aligned}
|
||||
D_{KL}(P||q) &= H(P,Q)-H(P) \\
|
||||
&= \sum_iP(x_i)log \frac{1}{Q(x_i)}-\sum_i P(x_i)log \frac{1}{P(x_i)} \\
|
||||
&= \sum_i P(x_i)log\frac{P(x_i)}{Q(x_i)} \\
|
||||
\end{aligned}
|
||||
\end{equation*}
|
||||
$
|
||||
|
||||
KL散度越小，两分布越接近。为了限制使用重要性采样的更新与采样策略分布差距不过大，即限制两策略分布的KL散度$D_{KL}(\pi_\theta||\pi_{\theta '})$小。TRPO就是用了这种方法。
|
||||
|
||||
**注意：PPO/TRPO这里的KL散度指的是两个策略（网络）的输出策略的分布。衡量两个网络之间参数的关系是无意义的！！！！**
|
||||
|
||||
#### 4. 信赖域方法
|
||||
|
||||
TRPO使用上一次策略$\pi_{\theta_{old}}$采样的数据来更新当前的策略$\pi_\theta$
|
||||
|
||||
通过限制KL散度来限制两策略分布差距
|
||||
|
||||
$$\mathop{\mathrm{maximize}}\limits_\theta\,\,\,{\hat {\mathbb{E}}_t[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta'(a_t|s_t)}}\hat A_t]}\\subject\,\,\,to\,\,\,\hat{\mathbb{E}}_t[KL[\pi_{\theta_{old}}(·|s_t)，\pi_\theta(·|s_t)]]\leq\delta \tag{8} $$
|
||||
|
||||
等价于无约束优化问题：
|
||||
|
||||
$$\mathop{\mathrm{maximize}}\limits_\theta\,\,\,{\hat {\mathbb{E}}_t[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta'(a_t|s_t)}}\hat A_t}-\beta KL[\pi_{\theta_{old}}(·|s_t)，\pi_\theta(·|s_t)]] \tag{9} $$
|
||||
|
||||
后续实验表明，简单地选择一个固定的惩罚系数β，用SGD优化惩罚目标方程$(9)$是不够的;还需要进行其他修改。
|
||||
|
||||
|
||||
|
||||
### 三. 近端策略优化PPO
|
||||
|
||||
#### 1. 近端优化裁剪（PPO-clip）
|
||||
|
||||
首先定义了$r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta _{old}}(a_t|s_t)},so\,\,\,r(\theta_{old})=1$,损失函数转化为：
|
||||
|
||||
$$L(\theta)=\hat{\mathbb{E}}_t[r_t(\theta) \hat A_t] \tag{10} $$
|
||||
|
||||
为了惩罚过大的策略更新，设计新的损失函数：
|
||||
|
||||
$$L^{CLIP}(\theta)=\hat{\mathbb{E}}_t[min(r_t(\theta) \hat A_t,clip(r_t(\theta),1-\epsilon,1+\epsilon)\hat{A}_t] \tag{11} $$
|
||||
|
||||
其中clip()函数指的是当$r_t(\theta)\in[1-\epsilon,1+\epsilon]$时，函数输出$r_t(\theta)$;当超出上/下界时，则输出上/下界。
|
||||
|
||||
这里如此改造损失函数是为了**限制损失函数在一定范围内**，从而**限制梯度**，最终**限制策略参数的更新幅度**，控制前后两次策略的分布差距，使得在使用上一次策略采样的样本更新有效。
|
||||
|
||||
PPO-clip方法并未使用KL散度，作者画图对比其他函数随着更新的变化情况
|
||||
|
||||
可见随着时间步增加，KL散度与损失函数均在增加，加了裁剪之后的损失函数可以维持在一定水平内。
|
||||
|
||||
作者通过实验发现，当$\epsilon=0.2$时效果最好。
|
||||
|
||||
#### 2. 自适应惩罚系数（PPO-pen）
|
||||
|
||||
传承TRPO的思想,使用KL散度来衡量新旧策略分布之间的差距。但是，这里使用了一个自适应的参数$\beta$,算法的具体流程为：
|
||||
|
||||
- 使用SGD优化器，损失函数
|
||||
|
||||
$L^{KLPEN}(\theta)={\hat {\mathbb{E}}_t[\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta'(a_t|s_t)}}\hat A_t}-\beta KL[\pi_{\theta_{old}}(·|s_t)，\pi_\theta(·|s_t)]]\tag{12} $
|
||||
|
||||
来进行策略的优化更新，并预先指定一个目标KL散度$d_{targ}$
|
||||
|
||||
- 计算$d=\hat{\mathbb{E}}_t[KL[\pi_{\theta_{old}}(·|s_t)，\pi_\theta(·|s_t)]]$更新惩罚系数$\beta$的值：
|
||||
|
||||
- 如果$d<d_{targ}/1.5,\beta=\beta/2$
|
||||
- 如果$d>d_{targ}×1.5,\beta=\beta×2$
|
||||
|
||||
这里的1.5和2都是启发式的超参数，目的就是当散度发生剧烈的变化时能够迅速的对惩罚系数进行调整以维持策略分布。实验表明该算法对前面说的超参数不敏感。而且能够对TRPO惩罚项中固定的超参数实现自适应调整，使算法性能大幅度提升。
|
||||
|
||||
#### 3.PPO算法总览
|
||||
|
||||
使用了重要性采样，PPO可以重复使用上一次的采样数据多次更新。将LossFunction更换为$L^{CLIP}\,\,or\,\,L^{KLPEN}$。
|
||||
|
||||
结合流行的方法，加入RL中的''正则化''$entropy bonus\,\,S[\pi_\theta](s_t)$（为了增加探索的能力）。计算advantage减少方差时候也会用到状态价值函数$V_\theta(s_t)$(有时策略与价值会共享网络)，所以增加了$L_{t}^{LF}(\theta)=(V_\theta(s_t)-V_t^{targ})^2$来训练网络能够学习估计出较为真实的状态价值函数。最后的损失函数就是如下形式：
|
||||
|
||||
$$L_t^{CLIP+VF+S}(\theta)=\hat{\mathbb{E}}_t[L_t^{CLIP}(\theta)-c_1L_t^{VF}(\theta)+c_2S[\pi_\theta](s_t)]\tag{13}$$
|
||||
|
||||
算法如下
|
||||
|
||||
|
||||
|
||||
### 四. 实验
|
||||
|
||||
#### 1. 对比不同损失函数之间的差距
|
||||
|
||||
作者对比了：不加裁剪与惩罚，裁剪，惩罚三种损失函数（这里并未使用状态价值函数共享结构与entropy bouns）即公式$(6),(10),(12)$在OpenAI MuJoCo physics engine任务上使用不同超参数的效果，结果如下：
|
||||
|
||||
|
||||
|
||||
在该任务上，PPO-clip算法获得了最高的分数，自适应惩罚系数分数略高于固定惩罚系数。
|
||||
|
||||
#### 2. 对比了其他连续控制算法
|
||||
|
||||
|
||||
|
||||
PPO-clip基本上超越了原有的算法。
|
||||
|
||||
#### 3. 成功使用PPO算法训练Humanoid Running and Steering
|
||||
|
||||
#### 4. 在其他Atari游戏上测试PPO算法并对比
|
||||
|
||||
### 五. 结论
|
||||
|
||||
我们引入了近端策略优化，这是一组利用多个随机梯度上升时期（一次采样多次利用）来执行每次策略更新的策略优化方法。这些方法具有TRPO的稳定性和可靠性，但实现起来要简单得多，只需要对普通策略梯度实现进行几行代码更改，适用于更一般的设置(例如，当为策略和值函数使用联合架构时)，并且具有更好的总体性能。
|
||||
|
||||
### 六、作者信息
|
||||
|
||||
于天琪，就读于哈尔滨工程大学陈赓实验班
|
||||
|
||||
知乎主页：https://www.zhihu.com/people/Yutianqi
|
||||
|
||||
qq:2206422122
|
||||
@@ -0,0 +1,168 @@
|
||||
## Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation
|
||||
## 使用 Kronecker 因子近似法的深度强化学习的可扩展信任区域方法
|
||||
|
||||
作者：Yuhuai Wu, Elman Mansimov, Roger B. Grosse, Shun Liao, Jimmy Ba
|
||||
|
||||
作者单位：University of Toronto Vector Institute，New York University
|
||||
|
||||
论文发表来源：Advances in Neural Information Processing Systems 30 (NIPS 2017)
|
||||
|
||||
论文发表时间：2017
|
||||
|
||||
论文查看网址：https://proceedings.neurips.cc/paper/2017/hash/361440528766bbaaaa1901845cf4152b-Abstract.html
|
||||
|
||||
论文贡献：本文扩展了自然政策梯度的框架，提出使用 Kronecker 因子近似曲率（K-FAC）与信任域来优化 actor 和 critic，作者称该方法为使用 Kronecker 因子信任域的actor-critic（ACKTR）。作者认为，这是第一个用于 actor-critic 方法的可扩展信任域自然梯度方法。该方法可以学习连续控制中的非平凡任务，也直接从原始像素输入中学习离散控制策略。作者在 Atari 游戏的离散领域以及 MuJoCo 环境的连续领域中测试了该方法。与以前 SOTA 的 actor-critic 方法相比，本文的方法获得了更高的奖励，采样效率平均提高 2-3 倍。
|
||||
|
||||
论文代码库：https://github.com/openai/baselines
|
||||
|
||||
### Motivation(Why)
|
||||
|
||||
1. 深度强化学习方法使用随机梯度下降 (SGD) 来训练控制策略。SGD 和相关的一阶方法对空间的探索效率不高，交互时间比较长。
|
||||
|
||||
2. 采样效率是强化学习的关注点之一，减小样本大小对于梯度更新是更高级的优化技术。
|
||||
|
||||
3. 自然梯度使用基于曲面的 Fisher 指标来做为度量梯度最陡下降方向的指标。自然策略梯度难以精确计算梯度，需要对 Fisher 信息矩阵求逆。TRPO 通过使用 Fisher 向量积避免了显示存储和对 Fisher 矩阵求逆。但是获取一步参数更新需要求多步共轭梯度，准确估计梯度需要每批都有大量数据样本。因此 TRPO 不适用于大模型，且样本效率很低。
|
||||
|
||||
4. Kronecker 因子近似曲率 (K-FAC) 是一种可扩展的自然梯度近似。在监督学习中，使用更大的 mini-batch 能加速各种最先进的大规模神经网络的训练。与 TRPO 不同的是，每次更新成本与 SGD 相当，保持了曲率信息的均值，允许使用小批量样本。由此表明，将 K-FAC 用于策略优化可以提高当前深度强化学习方法的样本效率。
|
||||
|
||||
### Main idea(What)
|
||||
|
||||
本文介绍了一种使用 Kronecker 因子信任域方法的 actor-critic 方法 (ACKTR)。该方法是针对 actor-critic 的可扩展信任域优化算法。该方法使用自然策略梯度的 Kronecker 因子，使得梯度的协方差矩阵能有效求逆。本文首次通过高斯-牛顿近似，扩展自然策略梯度算法来优化值函数。
|
||||
|
||||
### How
|
||||
|
||||
#### 1.背景知识
|
||||
|
||||
##### 1.1 强化学习和actor-critic方法
|
||||
|
||||
我们考虑一个与无限视界贴现马尔科夫决策过程互动的 智能体为一个五元组 $(X, A, \gamma, P, r)$。智能体的目标是最大化策略参数为 $\theta$ 的折扣累积回报的期望 $J(\theta)$。策略梯度方法直接参数化策略 $\pi_{\theta}(a \mid s_{t})$，更新 $\theta$ 以最大化目标 $J(\theta)$。策略梯度的一般形式定义为：
|
||||
|
||||
|
||||
|
||||
其中 $\psi^{t}$ 通常选用为优势函数 $A^{\pi}(s_{t},a_{t})$。本文参考异步优势 actor-critic(A3C) 方法来定义优势函数如下：
|
||||
|
||||
|
||||
|
||||
其中 $V^{\pi}_{\phi}(s_{t})$ 是值网络，$V^{\pi}_{t}(s_{t})=E_{\pi}[R_{t}]$。为值网络的参数，本文通过更新 TD ，来最小化自举 $k$ 步回报 $\hat{R}_{t}$ 和预测值之间的平方差，$\frac {1}{2}\left\|\hat{r}_{t} - V^{\pi}_{\phi}(s_{t})\right \|^{2}$.
|
||||
|
||||
##### 1.2 使用Kronecker因子近似的自然梯度
|
||||
|
||||
为了最小化非凸函数 $J(\theta)$，用最陡下降法计算更新 $\nabla \theta$，最小化 $J(\theta + \nabla \theta)$。然而欧氏范数的变化取决于参数 $\theta$，这是不合适的；因为模型的参数化是一个任意选择，不应该影响优化轨迹。自然梯度法利用 Fisher 信息矩阵 $F$ 构造范数- KL 散度的局部二次近似。该范数独立于概率分布类上的模型参数 $\theta$，提供了更稳定更有效的更新。但是由于神经网络可能包含数百万个参数，计算和存储精确的 Fisher 矩阵及其逆是不切实际的，因此需要借助近似值。Knonecker 因子近似曲率技术使用 Knonecker 因子近似能对 Fisher 矩阵的执行有效的近似自然梯度更新。细节看如下原文:
|
||||
|
||||
|
||||
|
||||
这种近似可以解释为假设激活和反向传播导数的二阶统计量是不相关的。有了这个近似，自然梯度更新可以有效计算。K-FAC 近似自然梯度更新只需要对与 $W$ 大小相当的矩阵进行计算。也有研究将 K-FAC 算法扩展到卷积网络及分布式网络，分布式 K-FAC 在训练大型现代分类卷积网络时速度提高了 2-3 倍。
|
||||
|
||||
#### 2. 方法
|
||||
|
||||
##### 2.1 actor-critic 中的自然梯度
|
||||
|
||||
为了定义强化学习目标的 Fisher 度量，本文使用策略函数，定义了给定当前状态下的动作分布，并在轨迹分布上取期望:
|
||||
|
||||
|
||||
|
||||
本文描述一种应用自然梯度来优化 critic 的方法。学习 critic 可以被认为是一个最小二乘函数近似问题，尽管这个问题的目标是移动的。在最小二乘函数近似中常用高斯-牛顿法。它将曲率近似为高斯-牛顿矩阵 $G:=E[J^{T}J]$ ，其中 $J$ 是映射参数到输出的 Jacobian 矩阵。高斯-牛顿矩阵等价于高斯观测模型的 Fisher 矩阵。这种等价性使得我们可将 K-FAC 也应用到 critic 上。假设 critic $v$ 的 Fisher 矩阵被定义为高斯分布 $p(v\mid s_{t})\sim N(v;V(s_{t},\sigma^{2}))$。critic 的 Fisher 矩阵是根据这个高斯输出分布定义的。 $\sigma$ 设为 1，这就是普通高斯-牛顿法。
|
||||
|
||||
如果 actor 和 critic 是分离的，可用上面定义的指标分别应用 K-FAC 更新。我们可以通过假设两个输出分布的独立性来定义策略分布和价值分布的联合分布，即 $p(a,v\mid s)=\pi(a\mid s)p(v\mid s)$ ，并构建关于 $p(a,v\mid s)$ 的 Fisher 度量。它与标准的 K-FAC 没有区别，只是我们需要独立对网络输出进行采样。然后我们可应用 K-FAC 近似 Fisher 矩阵 $E_{p(\tau)}[\nabla log p(a,v|s)\nabla log p(a,v|s)^{T}]$，来进行同步更新。
|
||||
|
||||
此外，作者还采用正则化技术。作者执行 Knonecker 近似所需的二阶统计量和逆的异步计算，以减少计算时间。
|
||||
|
||||
##### 2.2 步长选择和信任域优化
|
||||
|
||||
采用传统的自然梯度更新会导致算法过早收敛到一个接近确定性的策略。本文采用 K-FAC 的信任域公式，选择有效步长 $\eta$ 为
|
||||
|
||||
$$min(\eta_{max}, \sqrt{\frac{2\delta}{\nabla \theta^{T}\hat{F}\nabla \theta}})$$
|
||||
|
||||
其中学习率 $\eta$ 和信任域半径 $\delta$ 是超参数。如果 actior 和 critic 是分离的，这两个参数需要分别调参。
|
||||
|
||||
#### 3. 相关工作
|
||||
|
||||
自然梯度[1]由Kakade[10]首次应用于策略梯度方法。Bagnell 和 Schneider[3]进一步证明[10]中定义的度量是由路径分布流形推导出的协方差度量。Peters 和 Schaal[19]随后将自然梯度应用到 actor-critic 算法中。他们提出对 actor 的更新执行自然政策梯度，对 critic 的更新使用最小二乘时间差分 (LSTD) 方法。
|
||||
|
||||
然而，在应用自然梯度法时，有效存储 Fisher 矩阵和计算其逆存在着巨大的计算挑战。以前的工作限制了该方法使用兼容函数逼近器(线性函数逼近器)。为了避免计算负担，信任域策略优化 (TRPO)[21] 近似求解线性系统，使用共轭梯度和快速 Fisher 矩阵-向量乘积，类似于 Martens[13] 的工作。这种方法有两个主要缺点。首先，它需要重复计算 Fisher 向量积，不利于扩展到更大的架构，即用于从 Atari 和 MuJoCo 的图像观察中学习的实验。其次，它需要大量的短轨迹(rollout)，以便准确估计曲率。
|
||||
|
||||
K-FAC 通过使用易于处理的 Fisher 矩阵近似和在训练过程中保持曲率统计数据的运行平均值来避免这两个问题。尽管 TRPO 显示出比使用 Adam[11] 等一阶优化器训练的策略梯度方法更好的每次迭代进展，但它的样本效率通常较低。
|
||||
|
||||
几种提高 TRPO 计算效率的方法被陆续提出。为了避免重复计算 Fisher 向量乘积，Wang 等人[27]用策略网和当前策略网的运行平均值之间的KL散度的线性近似来解决约束优化问题。Heess 等[8]和 Schulman 等[23]在目标函数中添加 KL 代价作为软约束，而不是信任域优化器施加的硬约束。在连续和离散控制任务的样本效率方面，这两篇论文都显示了对普通策略梯度的一些改进。
|
||||
|
||||
最近还引入了其他 actor-critic 模型，通过引入经验重放[27]、[7]或辅助目标[9]来提高样本效率。这些方法与本文的工作是正交的，可以与 ACKTR 结合，进一步提高样本效率。
|
||||
|
||||
#### 4. 实验
|
||||
|
||||
本文进行了一系列实验来研究以下问题:
|
||||
|
||||
(1)在样本效率和计算效率方面，ACKTR 与最先进的 on-policy 方法和常用的二阶优化器基线相比如何?
|
||||
|
||||
(2)什么是更好的临界优化范数?
|
||||
|
||||
(3)与一阶方法相比，ACKTR 随 batch size 缩放的性能如何?
|
||||
|
||||
作者在两个标准基准测试平台上评估了提出的方法 ACKTR。作者采用Open AI Gym 中的任务环境做为评估基准。离散控制任务用 Atari2600 游戏模拟器做为评估基准；连续控制任务用 MuJoCo 物理引擎做为评估基准。进行对比的基线算法是 A2C 和 TRPO。ACKTR和基线算法采用相同的模型架构，除了 Atari 游戏上的 TRPO 基线，由于运行共轭梯度内循环的计算负担，作者只能使用更小的架构。
|
||||
|
||||
##### 4.1 离散控制
|
||||
|
||||
经过 1000 万时间步(1时间步等于4帧)训练的 6 款 Atari 游戏的结果如图 1 所示，阴影区域表示 2 个随机种子的标准差。与 A2C 和 TRPO2 相比较，在所有游戏中，ACKTR 在样本效率(即每时间步数的收敛速度)方面显著优于 A2C。作者发现 TRPO 只能在 1000 万时间步内学习两款游戏，即《Seaquest》和《Pong》，并且在样本效率方面表现不如A2C。
|
||||
|
||||
|
||||
|
||||
表 1 是在六款 Atari 2600 游戏上对离散控制任务的实验评估数据。ACKTR 和 A2C 结果显示在 5000 万时间步后获得的最后 100 个平均回合奖励，以及在 1000 万时间步后获得的 TRPO 结果。表格中还显示了第 $N$ 个回合，其中 $N$ 表示第 $N$ 到第 $(N + 100)$ 个游戏的平均奖励超过人类表现水平[16]的第 1 回合，平均超过 2 个随机种子。在《Beamrider》、《Breakout》、《Pong》和《Q-bert》等游戏中，A2C 需要比 ACKTR 多2.7、3.5、5.3 和 3.0 倍的回合才能达到人类的表现。此外，在《太空入侵者》中，A2C的运行结果不如人类的表现，而 ACKTR 的平均成绩是 19723，是人类表现(1652)的 12倍。在《Breakout》、《Q-bert》和《Beamrider》中，ACKTR 获得的回合奖励分别比 A2C高出 26%、35% 和 67%。
|
||||
|
||||
作者还在 Atari 的其他游戏中评估了 ACKTR，完整结果见原文附录。作者将 ACKTR 与 Q-learning 方法进行了比较，发现在 44 个基准中有 36 个，ACKTR 在样本效率方面与 Q-learning 方法相当，并且消耗的计算时间大大减少。
|
||||
|
||||
|
||||
|
||||
如图 2 所示，在《亚特兰蒂斯》游戏中，ACKTR 很快就学会了在 1.3 小时( 600 集)内获得 200 万的奖励。A2C 花了 10 个小时( 6000 集) 才达到同样的性能水平。
|
||||
|
||||
|
||||
|
||||
##### 4.2 连续控制
|
||||
|
||||
作者在 MuJoCo 中进行连续控制任务的模拟。由于高维动作空间和探索，连续控制任务有时更具挑战性。经过 100 万个时间步训练的 8 个 MuJoCo 环境的结果如图 3 所示（阴影区域表示 3 个随机种子的标准差。）。本文的模型在 8 个 MuJoCo 任务中的 6 个任务上显著优于基线，在其他两个任务 (Walker2d 和 Swimmer) 上与 A2C 差不多。
|
||||
|
||||
|
||||
|
||||
如表2所示，ACKTR 在所有任务上更快地达到指定的阈值，除了Swimmer, TRPO 的样本效率是 TRPO 的 4.1 倍。一个特别值得注意的例子是 Ant，其中 ACKTR 的样本效率是 TRPO 的 16.4 倍。在平均奖励分数方面，除了 TRPO 在 Walker2d 环境下的奖励分数高出 10% 外，其他三种模型表现相当。
|
||||
|
||||
|
||||
|
||||
作者还尝试直接从像素来学习连续控制策略。从像素学习连续控制策略比从状态空间学习更具挑战性，部分原因是与 Atari 相比渲染时间较慢(MuJoCo为0.5秒，Atari为0.002秒)。最先进的 actor-critic 方法 A3C[17]只报告了相对简单任务的像素结果，如 Pendulum、 Pointmass2D 和 Gripper。如图4所示。可以看到，在经过 4000 万时间步训练后，ACKTR模型在最终回合奖励方面明显优于 A2C。更具体地说，在 Reacher、HalfCheetah 和 Walker2d 上，本文模型获得的最终奖励是 A2C 的 1.6 倍、2.8 倍和1.7 倍。
|
||||
|
||||
|
||||
|
||||
从像素训练策略的视频： https: //www.youtube.com/watch?v=gtM87w1xGoM
|
||||
|
||||
预训练的模型权重：https: //github.com/emansim/acktr。
|
||||
|
||||
|
||||
##### 4.3 是一个优化critic的更好范式吗？
|
||||
|
||||
之前的自然策略梯度方法只对 actor 应用自然梯度更新，本文作者还建议对 critic 应用自然梯度更新。区别只在于选用什么范式来对 critic 进行最快的梯度下降;即2.2节中定义的范式 $\left \| \cdot \right \| _{B}$。此处将 ACKTR 应用于 actor，并比较了使用一阶方法(即欧氏范数)和使用 ACKTR (即高斯-牛顿定义的范数)进行临界优化。图5 (a)和(b)显示了连续控制任务《HalfCheetah》和 Atari 游戏《Breakout》的结果。作者观察到，无论使用哪种范式来优化 critic，与基线 A2C 相比，对 actor 应用 ACKTR 都会带来改进。
|
||||
|
||||
|
||||
|
||||
然而，使用高斯-牛顿范数优化 critic 所带来的改进在训练结束时的样本效率和回合奖励方面更为显著。此外,高斯-牛顿范数也有助于稳定训练。作者发现自适应高斯-牛顿算法并没有比普通的高斯-牛顿算法提供任何显著的改进。
|
||||
|
||||
##### 4.4 ACKTR在挂钟时间上与A2C相比如何?
|
||||
|
||||
作者将 ACKTR 与基准 A2C 和 TRPO 进行了比较。表 3 显示了 6 个 Atari 游戏和 8 个 MuJoCo (来自状态空间)环境下的平均每秒时间步数。所得结果与之前的实验设置相同。注意，在 MuJoCo 中，任务回合是按顺序处理的，而在 Atari 环境中，回合是并行处理的;因此更多的帧是在 Atari 环境中处理的。从表中我们可以看到， ACKTR 比 A2C 最多只增加 25% 的计算时间，证明了它的实用性和很大的优化效益。
|
||||
|
||||
|
||||
|
||||
##### 5.5 ACKTR和A2C在不同批处理大小下的表现如何?
|
||||
|
||||
作者比较了 ACKTR 和基线 A2C 在不同 batch size 下的表现。我们分别试验了 160 和 640 的 batch size。图 5 (c) 显示了以时间步数表示的奖励。
|
||||
|
||||
|
||||
|
||||
图五(a)和(b)比较了用高斯-牛顿范数(ACKTR)和欧氏范数(一阶)来优化 critic (值网络)。(c)和(d)比较不同 batch size 的 ACKTR 和 A2C 。
|
||||
|
||||
作者发现，batch size 较大的 ACKTR 与 batch size 较小的 ACKTR 表现一样好。但是，随着 batch size 的增加，A2C 的样本效率下降明显。这与图 5 (d) 中的观察结果相对应，在图 5 (d) 中，我们根据更新次数绘制了训练曲线。我们发现，与使用 A2C 相比，使用更大 batch size 的 ACKTR 的好处大大增加。这表明，在分布式设置中，ACKTR 有很大的加速潜力，在这种情况下，需要使用大的 mini-batch。
|
||||
|
||||
#### 5. 结论
|
||||
|
||||
本文提出了一个用于深度强化学习的样本效率高且计算成本低的信任域优化方法。作者使用一种称为 K-FAC 的技术，对 actor-critic 方法近似自然梯度更新，并对稳定性进行信任域优化。本文第一个提出使用自然梯度更新来优化 actor-critic。作者在 Atari 游戏和MuJoCo 环境中测试了 ACKTR 方法，观察到与一阶梯度方法 (A2C) 和迭代二阶方法 (TRPO) 相比，样本效率平均提高了 2 到 3 倍。由于本文算法的可扩展性，该方法也是第一个直接从原始像素观测空间训练连续控制的几个非平凡任务的技术。
|
||||
|
||||
#### 个人总结
|
||||
本文针对 TRPO 样本效率不高，不易扩展的问题，结合自然策略梯度 kronecker 因子近似技术，提出了带有信任域的 knonecker 因子近似技术，用于优化 actor-critic 方法。本文方法通过离散控制和连续控制实验表明，明显提高了样本效率和可扩展性。
|
||||
|
||||
汪莉娟：天津大学研究生，专业方向为控制科学与工程，主要研究方向为交通优化与智能控制。
|
||||
@@ -0,0 +1,173 @@
|
||||
# SAC算法
|
||||
|
||||
原论文：[Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor](https://arxiv.org/abs/1801.01290)
|
||||
|
||||
SAC算法是off-policy算法，此前的off-policy算法存在采样复杂性高和难收敛的问题，使得超参数十分敏感，SAC算法通过在最大预期return的同时最大化熵值，也就是尽量获得最高累计收益的同时保持探索避免过早掉入局部最优解。SAC结合已有的off-policy模型actor-critic框架使得在不同的随机种子上都能达到SOTA效果。
|
||||
|
||||
## 介绍
|
||||
|
||||
深度强化学习的快速发展，给机器人控制领域带来了许多进展。此前的工作中，面向连续控制任务的算法有TRPO、PPO、DDPG等算法。
|
||||
|
||||
PPO是一种on-policy面向离散和连续控制的算法，在许多数据集上取得了较好的效果，但是存在严重的采样效率低下的问题，这对于真实环境中的控制问题采样花费来说是难以接受的；DDPG是一种off-policy的面向连续控制的问题，比PPO采样效率高但是DDPG训练了一种确定性策略（deterministic policy），在每个状态下只选择一个最优的动作，这样很容易掉入局部最优解的情况。
|
||||
|
||||
在连续控制问题中，SAC算法结合已有actor-critic框架，使用随机策略（stochastic policy）最大累计收益的同时也保持熵值最大化，提升了采样效率增强了智能体的探索能力，避免了过早陷入局部最优解的情况，同时也增强了模型在不同初始环境的泛化能力和鲁棒性。
|
||||
|
||||
## 预备知识
|
||||
|
||||
### 最大熵强化学习
|
||||
|
||||
传统的强化学习是最大化累计回报值：
|
||||
$$
|
||||
J(\pi)=\sum_t\mathbb{E}_{(s_t,a_t)\sim\rho_\pi}[r(s_t,a_t)]
|
||||
$$
|
||||
而最大熵的RL算法的目标函数为：
|
||||
$$
|
||||
J(\pi)=\sum^{T}_{t=0}\mathbb{E}_{(s_t,a_t)\sim\rho_\pi[r(s_t,a_t)+\alpha\mathcal{H}(\pi(\cdot|s_t))]}
|
||||
$$
|
||||
其中$\alpha$为熵的温度系数超参数，用于调整对熵的重视程度。$\mathcal{H}(\pi(\cdot|s_t))$是熵值，可表示为$\mathcal{H}(\pi(\cdot|s_t))=-\mathbb{E}_{s_t}[\log \pi(\cdot|s_t)]$。
|
||||
|
||||
在累计回报值中加入熵值的目的是使策略随机化（stochastic），在遇到一个state有多个同样优秀的动作时鼓励探索，可以随机从这些动作中选出一个形成trajectory，而不是总选择同一个确定性策略（deterministic）导致模型最终无法学到全局最优解。
|
||||
|
||||
## Soft policy Iteration
|
||||
|
||||
在model-free强化学习policy iteration中，常将策略更新过程分为policy evaluation和policy improvement两个阶段。
|
||||
|
||||
### Soft policy evaluation
|
||||
|
||||
标准的Q function：
|
||||
$$
|
||||
Q^\pi(s,a)=r(s,a)+\gamma\mathbb{E}_{(s^\prime,a^\prime)\sim\rho_\pi}[Q(s^\prime,a^\prime)]
|
||||
$$
|
||||
标准的V function：
|
||||
$$
|
||||
V^\pi(s)=\mathbb{E}_{(s_t,a_t)\sim\rho_\pi}[Q(s^\prime,a^\prime)]
|
||||
$$
|
||||
在标准的方程中引入熵得到Soft Value Function：
|
||||
|
||||
Soft Q function:
|
||||
$$
|
||||
Q^\pi_{soft}(s,a)=r(s,a)+\gamma\mathbb{E}_{(s^\prime,a^\prime)\sim\rho_\pi}[Q(s^\prime,a^\prime)-\alpha\log(\pi(a^\prime|s^\prime))]
|
||||
$$
|
||||
Soft V function:
|
||||
$$
|
||||
V^\pi_{soft}(s^\prime)=\mathbb{E}_{(s^\prime,a^\prime)\sim\rho_\pi}[Q_{soft}(s^\prime,a^\prime)-\alpha\log(\pi(a^\prime|s^\prime))]
|
||||
$$
|
||||
由此可得Soft Q和V的Bellman方程：
|
||||
$$
|
||||
Q^\pi_{soft}(s,a)&=&r(s,a)+\gamma\mathbb{E}_{(s^\prime,a^\prime)\sim\rho_\pi}[Q(s^\prime,a^\prime)-\alpha\log(\pi(a^\prime|s^\prime))]\\
|
||||
&=&r(s,a)+\gamma\mathbb{E}_{s^\prime\sim\rho}[V^\pi_{soft}(s^\prime)]
|
||||
$$
|
||||
在固定policy下，使用soft Bellman equation更新Q value直到收敛。
|
||||
|
||||
### Soft policy improvement
|
||||
|
||||
stochastic policy的重要性：面对多模的（multimodal）的Q function，传统的RL只能收敛到一个选择（左图），而更优的办法是右图，让policy也直接符合Q的分布。
|
||||
|
||||
|
||||
|
||||
为了适应更复杂的任务，MERL中的策略不再是以往的高斯分布形式，而是用基于能量的模型（energy-based model）来表示策略:
|
||||
$$
|
||||
\pi(a_t|s_t)\propto exp(-\mathcal{E}(s_t,a_t))
|
||||
$$
|
||||
为了让EBP和值函数联系起来，设置$\mathcal{E}(s_t,a_t)=-\frac{1}{\alpha}Q_{soft}(s_t,a_t)$，因此$\pi(a_t|s_t)\propto exp(-\frac{1}{\alpha}Q_{soft}(s_t,a_t))$
|
||||
|
||||
由soft v function变形可得：
|
||||
$$
|
||||
\pi(s_t,a_t)&=&exp(\frac{1}{\alpha}Q_{soft}(s_t,a_t)-V_{soft}(s_t))\\
|
||||
&=&\frac{exp(\frac{1}{\alpha}Q_{soft}(s_t,a_t)}{exp(\frac{1}{\alpha}V_{soft}(s_t))}
|
||||
$$
|
||||
定义softmax（注意此处softmax和神经网络不同，神经网络中的softmax实际上是求分布的最大值soft argmax）
|
||||
$$
|
||||
softmax_af(a):=\log\int expf(a)da
|
||||
$$
|
||||
因此$V_{soft}(s_t)=\alpha softmax_a(\frac{1}{\alpha}Q_{soft}(s_t,a_t))$，
|
||||
|
||||
根据Soft Q function可化为softmax形式：
|
||||
$$
|
||||
Q_{soft}(s_t,a_t)=\mathbb{E}[r_t+\gamma softmax_aQ(s_{t+1},a_{t+1})]
|
||||
$$
|
||||
因此整个Policy Iteration流程可总结为：
|
||||
|
||||
**soft policy evaluation:**固定policy，使用Bellman方程更新Q值直到收敛
|
||||
$$
|
||||
Q^\pi_{soft}(s,a)=r(s,a)+\gamma\mathbb{E}_{(s^\prime,a^\prime)\sim\rho_\pi}[Q(s^\prime,a^\prime)-\alpha\log(\pi(a^\prime|s^\prime))]
|
||||
$$
|
||||
**soft policy improvement:**更新policy
|
||||
$$
|
||||
\pi^\prime=\arg\min_{\pi_k\in \prod}D_{KL}(\pi_k(\cdot|s_t)||\frac{exp(\frac{1}{\alpha}Q^\pi_{soft}(s_t,\cdot))}{Z_{soft}^\pi(s_t)})
|
||||
$$
|
||||
|
||||
|
||||
## Soft Actor-Critic框架
|
||||
|
||||
|
||||
|
||||
SAC算法的构建首先是神经网络化，我们用神经网络来表示Q和Policy：$Q_\theta(s_t,a_t)$ 和 $\pi_\phi(a_t|s_t)$。Q网络比较简单，几层的MLP最后输出一个单值表示Q就可以了，Policy网络需要输出一个分布，一般是输出一个Gaussian包含mean和covariance。下面就是构建神经网络的更新公式。
|
||||
|
||||
### Critic
|
||||
|
||||
构造两个Q网络，参数通过每次更新Q值小的网络参数，Q网络的损失函数为：
|
||||
$$
|
||||
J_Q(\theta)=\mathbb{E}_{(s_t,a_t,s_{t+1})\sim \mathcal{D}}[\frac{1}{2}(Q_\theta(s_t,a_t)-(r(s_t,a_t)+\gamma V_{\bar{\theta}}(s_{t+1})))^2]
|
||||
$$
|
||||
$\bar{\theta}$是target soft Q网络的参数，带入V的迭代表达式：
|
||||
$$
|
||||
J_Q(\theta)=\mathbb{E}_{(s_t,a_t,s_{t+1})\sim \mathcal{D}}[\frac{1}{2}(Q_\theta(s_t,a_t)-(r(s_t,a_t)+\gamma (Q_{\bar \theta}(s_{t+1},a_{t+1})-\alpha\log(\pi(a_{t+1}|s_{t+1})))))^2]
|
||||
$$
|
||||
|
||||
### Actor
|
||||
|
||||
Policy网络的损失函数为：
|
||||
$$
|
||||
J_\pi(\phi)&=&D_{KL}(\pi_k(\cdot|s_t)||\frac{exp(\frac{1}{\alpha}Q^\pi_{soft}(s_t,\cdot))}{Z_{soft}^\pi(s_t)})\\
|
||||
&=&\mathbb{E}_{s_t\sim\mathcal{D},a\sim\pi_\phi}[\log\pi_\phi(a_t|s_t)-\frac{1}{\alpha}Q_\theta(s_t,a_t)+\log Z(s_t)]
|
||||
$$
|
||||
其中策略网络的输出是一个动作分布，即高斯分布的均值和方差，这里的action采用重参数技巧来获得，即：
|
||||
$$
|
||||
a_t=f_\phi(\epsilon_t;s_t)=f^\mu_\phi(s_t)+\epsilon_t\cdot f^\mu_\phi(s_t)
|
||||
$$
|
||||
|
||||
### Update temperature
|
||||
|
||||
前面的SAC中，我们只是人为给定一个固定的temperature$\alpha$作为entropy的权重，但实际上由于reward的不断变化，采用固定的temperature并不合理，会让整个训练不稳定，因此，有必要能够自动调节这个temperature。当policy探索到新的区域时，最优的action还不清楚，应该调高temperature 去探索更多的空间。当某一个区域已经探索得差不多，最优的action基本确定了，那么这个temperature就可以减小。
|
||||
|
||||
通过构造一个带约束的优化问题，让熵权重在不同状态下权重可变，得到权重的loss：
|
||||
$$
|
||||
J(\alpha)=\mathbb{E}_{a_t\sim\pi_t}[-\alpha \log \pi_t(a_t|\pi_t)-\alpha\mathcal{H}_0]
|
||||
$$
|
||||
soft actor-critic算法用伪代码可表示为：
|
||||
|
||||
<img src="img/SAC_3.png" alt="image-20221114144621522" style="zoom:50%;" />
|
||||
|
||||
## 实验
|
||||
|
||||
|
||||
|
||||
在连续控制的benchmark上表现效果比大多数SOTA算法（DDPG、PPO、SQL、TD3）好。
|
||||
|
||||
## 总结
|
||||
|
||||
基于最大熵的强化学习算法优势：
|
||||
|
||||
1）学到policy可以作为更复杂具体任务的初始化。因为通过最大熵，policy不仅仅学到一种解决任务的方法，而是所有all。因此这样的policy就更有利于去学习新的任务。比如我们一开始是学走，然后之后要学朝某一个特定方向走。
|
||||
|
||||
2）更强的exploration能力，这是显而易见的，能够更容易的在多模态reward （multimodal reward）下找到更好的模式。比如既要求机器人走的好，又要求机器人节约能源。
|
||||
|
||||
3）更robust鲁棒，更强的generalization。因为要从不同的方式来探索各种最优的可能性，也因此面对干扰的时候能够更容易做出调整。（干扰会是神经网络学习过程中看到的一种state，既然已经探索到了，学到了就可以更好的做出反应，继续获取高reward）。
|
||||
|
||||
虽然SAC算法采用了energy-based模型，但是实际上策略分布仍为高斯分布，存在一定的局限性。
|
||||
|
||||
====================================
|
||||
|
||||
作者：杨骏铭
|
||||
|
||||
研究单位：南京邮电大学
|
||||
|
||||
研究方向：强化学习、对抗学习
|
||||
|
||||
联系邮箱：jmingyang@outlook.com
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
278
papers/Policy_gradient/Trust Region Policy Optimization.md
Normal file
278
papers/Policy_gradient/Trust Region Policy Optimization.md
Normal file
@@ -0,0 +1,278 @@
|
||||
## Trust Region Policy Optimization
|
||||
## （信任域策略优化）
|
||||
作者:John Schulman, Sergey Levine, Pieter Abbeel, Michael Jordan, Philipp Moritz
|
||||
|
||||
作者单位：University of California, Berkeley, Department of Electrical Engineering and Computer Sciences
|
||||
|
||||
论文发表来源：Proceedings of the 32nd International Conference on Machine Learning, PMLR 37:1889-1897
|
||||
|
||||
论文发表时间：2015
|
||||
|
||||
论文查看网址：https://proceedings.mlr.press/v37/schulman15.html
|
||||
|
||||
论文贡献：本文通过对理论证明的方案进行一些近似，开发了一种保证单调改进优化控制策略的方法，称为信任域策略优化(TRPO)。该方法的近似偏离了理论，但是侧重于给出单调改进，几乎不需要调整超参数。该方法适用于神经网络等大型非线性策略的优化。本文通过模拟机器人和Atari游戏的实验既证明了该方法在各种任务中表现很稳健，也为未来训练结合感知和控制的机器人控制器提供一个可能的统一方案。该方法降低了样本复杂度，为后续的复杂策略学习任务提供了算法基础。简单来说，本文的单调改进方法将难以应用的策略梯度优化理论变成了可以实际应用的策略梯度优化算法。
|
||||
|
||||
### Motivation(why):
|
||||
|
||||
基于梯度的优化算法比无梯度优化算法有更好的样本复杂度，但是在连续控制问题中，基于梯度的方法对于无梯度随机搜索的表现并不令人满意。在具有大量参数的监督学习任务中，连续梯度优化对于学习函数的逼近表现非常成功。如果将连续梯度优化扩展到强化学习，将能更有效的学习出复杂而强大的控制策略。
|
||||
|
||||
### Main Idea(what)
|
||||
|
||||
本文首先证明了最小化某个代理损失函数保证了策略改进与非平凡补偿，然后对理论证明的算法进行一系列逼近，得到一个实用的算法，本文称之为信任域策略优化。本文描述了该算法的两个变体：一个是可应用于无模型设置的单路径方法，另一个是vine方法，该方法要求系统恢复到特定状态，这通常只在仿真中可能。这些算法是可扩展的，可以优化具有成千上万个参数的非线性策略。这在以前是无模型策略搜索的主要挑战。
|
||||
|
||||
### How
|
||||
|
||||
#### 1. 前提
|
||||
|
||||
将一个无限水平贴现马尔科夫决策过程(MDP)定义为一个元组 $<S,A,P,c,\rho_{0},\gamma>$，$S$ 是有限状态集，$A$ 是有限动作集，$P:S\times A\times S \to R$ 是转移概率分布，$c:S\to R$ 是代价函数，$\rho_{0}:S\to R$ 是初始状态 $s_{0}$ 的分布，$\gamma \in(0,1)$ 是折扣因子。
|
||||
|
||||
令 $\pi$ 表示随机策略 $\pi:S\times A \to [0,1]$，令 $\eta(\pi)$ 表示期望折扣代价，则有：
|
||||
|
||||
|
||||
|
||||
状态动作值函数 $Q_{\pi}$ ,值函数 $V_{\pi}$ ,优势函数 $A_{\pi}$ 标准定义如下：
|
||||
|
||||
|
||||
|
||||
则随着时间步的累积，根据 $\pi\$ 的优势表达了另一个策略 $\tilde{\pi}$ 的期望代价如公式(1):
|
||||
|
||||
|
||||
|
||||
令$\rho_{\pi}$为非归一化的折扣访问频率，则
|
||||
|
||||
|
||||
|
||||
将公式(1)重新排列为对状态求和，则有公式(2):
|
||||
|
||||
|
||||
|
||||
这个公式意味着对于任意策略更新 $\pi \to \tilde{\pi}$ 保证减少 $\eta$,或在期望优势处处为 $0$ 的情况下使其保持不变，$\tilde{\pi}$ 在每个状态 $s$ 都有一个非正的期望优势，即 $\sum_{a}\tilde{\pi}(a|s)A(\pi)(s,a)\le 0$。这意味着由精确策略迭代执行更新的经典结果。然而，在近似设置中，由于估计和近似误差，某些状态的预期优势为正通常是不可避免的，即 $\sum_{a}\tilde{\pi}(a|s)A(\pi)(s,a)\ge 0$。
|
||||
$\rho_{\tilde{\pi}}$ 对 $\tilde{\pi}$ 的复杂依赖使得公式(2)难以直接优化。于是本文引入下面对 $\eta$ 的局部逼近：
|
||||
|
||||
|
||||
|
||||
然而，如果我们有一个参数化的策略 $\pi_{\theta}$ ,其中 $\pi_{\theta}(a|s)$ 是参数向量 $\theta$ 的可微函数，则 $L_{\pi}$ 对 $\eta$ 到一阶。那就是说，对于任意参数值 $\theta_{0}$，有
|
||||
|
||||
|
||||
|
||||
公式(4)表明能改进 $L_{\pi_{old}}$ 的充分小一步更新 $\pi_{\theta_{0}}\to \tilde(\pi)$ 也能改进 $\eta$ ,但是我们无法知道这一步的大小如何。为解决该问题，Kakade & Langford (2002)提出一种保守策略迭代的策略更新方案，为 $\eta$ 的改进提供了明确的下界。
|
||||
|
||||
为定义保守策略迭代更新，令 $\pi_{old}$ 表示当前策略，假设可解 $\pi'=argmin_{\pi'}L_{\pi_{old}}(\pi')$ 。新策略 $\pi_{new}$ 取为混合策略，如公式(5)：
|
||||
|
||||
|
||||
|
||||
Kakade and Langford证明了这个更新的下述结果：
|
||||
|
||||
|
||||
|
||||
$\epsilon$是$\pi'$相对于$\pi$的最大优势(或正或负)，等式(6)给出了更简单的界。这个界当$\alpha \ll 1$时有点弱。这个界只适用于等式(5)生成的混合策略。混合策略不适用于实际情况，对于所有一般随机策略需要一个实际的策略更新方案。
|
||||
|
||||
#### 2. 一般随机策略的单调改进保证
|
||||
|
||||
公式(6)意味着改进公式右边就能保证改进真实的期望代价目标 $\eta$。本文的主要理论结果是，通过用 $\pi$ 和 $\tilde{\pi}$ 之间的距离度量来替换 $\alpha$，公式(6)中的策略改进边界可以扩展到一般的随机策略，而不是仅适合于混合策略。这一结果对于将改进保证扩展到实际问题是至关重要的。对于离散概率分布 $p,q$ ，定义两个策略之间的总变分散度为：
|
||||
|
||||
|
||||
|
||||
定理1.令 $\alpha=D^{max}_{TV}(\pi_{old},\pi_{new})$，令 $\epsilon=max_{s}\left | E_{a\sim\pi'(a|s)}[A_{\pi}(s,a)]\right |$，则公式(8)成立。证明在附录。
|
||||
|
||||
我们注意到变分散度和KL散度之间有这样的关系：$D_{TV}(p||q)^2 \le D_{KL}(p||q)$。令 $D^{max}_{KL}(\pi, \tilde{\pi}) = max_{s}D_{KL}(\pi(\cdot|s))$，可从公式(8)直接推导出下面的界，即公式(10):
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
算法1描述了基于公式(10)中策略改进边界的近似策略迭代方法。注意，我们假设了优势值$A_{\pi}$ 的精确评估。
|
||||
|
||||
由公式(10)可知，算法1保证生成一系列单调改进策略 $\eta(\pi_{0})\ge\eta(\pi_{1})\eta(\pi_{2})\ge ...$。令
|
||||
|
||||
|
||||
|
||||
通过每次迭代中最小化 $M_{i}$，我们可以保证真正的目标 $\eta$ 是不增加的。这个算法是一种majorization-minimization(MM)算法，这是一类包括期望最大化的方法。在MM算法中，$M_{i}$ 是代理函数，优化 $\eta$ 等于 $\pi_{i}$ 。该算法也联想到近端梯度法和镜像下降法。下一节中提出的信任域策略优化是算法1的近似，算法1使用对KL发散的约束而不是惩罚来健壮的允许大的更新。
|
||||
|
||||
#### 3.参数化策略的优化
|
||||
本节讲述了在有限样本数和任意参数化的基础上，如何从理论基础得出一个应用算法。
|
||||
因为我们用参数向量 $\theta$ 考虑了参数化策略 $\pi_{\theta}(a|s)$，因此我们用函数 $\theta$ 而不是 $\pi$ 重载以前的策略表示。优化目标为下式：
|
||||
|
||||
|
||||
|
||||
如果采用上式的惩罚系数 $C$ ，步长会非常小，以稳健方式采取更大步骤的一种方法是对新旧策略之间的KL散度使用约束，即信任域约束，如公式(12):
|
||||
|
||||
|
||||
|
||||
公式(12)强加了约束条件，即KL散度在状态空间的每个点上都是有界的。本文使用一种考虑平均KL散度的启发式近似：
|
||||
|
||||
|
||||
|
||||
由此将生成策略更新的优化问题变为公式(13):
|
||||
|
||||
|
||||
|
||||
类似的策略更新在以前的工作中已被提出，本文实验中也与以前的方法做了比较。实验表明，这种类型的约束更新与公式(12)中的最大KL散度约束具有相似的实验性能。
|
||||
|
||||
#### 4.基于采样的目标估计和约束
|
||||
|
||||
本节描述了如何使用蒙特卡洛模拟逼近目标函数和约束函数。公式(13)通过扩展 $L_{\theta_{old}}$ 可有公式(14):
|
||||
|
||||
|
||||
|
||||
用期望 $frac{1}{1-\gamma}E_{s\sim\rho_{old}}[...]$ 代替 $\sum_{s}\rho_{\theta_{old}}[...]$，用优势值 $A_{\theta_{old}}$ 代替Q值 $Q_{\theta_{old}}$。最后用一个重要性采样估计量代替动作的和，用 $q$ 表示采样分布，则单个 $s_{n}$ 对损失函数贡献为：
|
||||
|
||||
|
||||
|
||||
则公式(14)中的优化问题完全等价于公式(15)中用期望表示的优化问题：
|
||||
|
||||
|
||||
|
||||
剩下的就是用样本均值代替期望，用经验估计代替Q值。
|
||||
|
||||
执行此估计，本文给出两种不同方法：
|
||||
|
||||
* 第一种称为单路径采样方法，典型用于策略梯度估计，它基于对个体轨迹的采样。
|
||||
|
||||
* 第二种称为vine方法，它构建一个展开(rollout)集，然后从展开集中的每个状态执行多个操作。这种方法主要用于策略迭代方法。
|
||||
|
||||
##### 4.1 单路径方法
|
||||
|
||||
通过采样 $s_{0}\sim \rho_{0}$ 收集状态序列，然后模拟策略 $\pi_{\theta_{old}}$ 一定量的时间步后产生轨迹 $s_{0},a_{0},s_{1},a_{1},...,s_{T-1},a_{T-1},s_{T}$。即有 $q(a|s)=\pi_{\theta_{old}}(a|s)$。在每个 $(s_{t},a_{t})$ 上沿轨迹取未来成本折扣和来计算 $Q_{\theta_{old}}(s,a)$。
|
||||
|
||||
##### 4.2 vine方法
|
||||
|
||||
采样 $s_{0}\sim \rho_{0}$，模拟策略 $\pi_{\theta_{old}}$ 生成许多轨迹，沿轨迹选取有 $N$ 个状态的子集 $s_{1},s_{2},...,s_{N}$，本文称之为“rollout集”(展开集)。在该集合中，对于每个状态 $s_{n}$，根据 $a_{n,k}\sim q(\cdot|s_{n})$ 采样 $K$ 个动作。本文发现 $q(\cdot|s_{n}=\pi_{\theta_{i}}(\cdot|s_{n})$ 在机器人动作训练的连续问题上表现很好，均匀分布在像Atari游戏这样的离散任务上能有更好的探索。
|
||||
|
||||
对于在每个状态 $s_{n}$ 采样的每个动作 $a_{n,k}$,，我们通过执行从状态 $s_{n}$ 和动作 $a_{n,k}$ 开始的rollout(即一个短轨迹)来估计 $\hat{Q}_{\theta_{i}}(s_{n},a_{n,k})$。我们可以通过使用相同的随机数序列（即公共随机数）来处理 $K$个段短轨迹中的噪声，极大地减少了短轨迹之间 $Q$ 值差异的方差。
|
||||
|
||||
在小的有限动作空间中，我们可以从给定的状态为每一个可能的动作生成一个短轨迹(rollout)。从单个状态 $s_{n}$ 对 $L_{\theta_{old}}$ 的贡献如下:
|
||||
|
||||
|
||||
|
||||
在大的或连续状态空间中，我们利用重要抽样来构造代理损失的估计量。单个状态 $s_{n}$ 的自归一化估计量为
|
||||
|
||||
|
||||
|
||||
假设我们执行了来自状态 $s_{n}$ 的 $K$个动作 $a_{n,1}, a_{n,2}，…， a_{n,K}$ 来自状态sn。这种自归一化估计器消除了对 $Q$ 值使用基线的需要(向q值添加一个常数，梯度不变)。对 $s_{N}\sim \rho(\pi)$ 求平均值，可以得到 $L_{\theta_{old}}$ 的估计量，以及它的梯度。
|
||||
|
||||
图1说明了vine方法和单路径方法。
|
||||
|
||||
|
||||
|
||||
左图为单路径程序示意图。通过模拟策略生成一组轨迹，并将所有状态-动作对 $(s_{n}, a_{n})$ 合并到目标中。右图为vine方法示意图。生成一组“主干”轨迹，然后从到达状态的子集生成“分支”展开。对于每个状态 $s_{n}$，执行多个操作(这里是 $a_{1}$ 和 $a_{2}$)，并在每个操作之后执行一次短轨迹，使用公共随机数(CRN)来减少方差。
|
||||
|
||||
vine方法中用于采样的轨迹可以被比作藤蔓的茎，它在不同的点(短轨迹集)上分成几个短分支(展开轨迹)。
|
||||
|
||||
在替代损失的 $Q$ 值样本数量相同的情况下，vine方法优于单一路径方法，对目标的局部估计具有更低的方差。即vine法对优势值给出了更好的估计。vine方法的缺点是对这些优势估计，必须对模拟器执行更多的调用。此外，vine方法要求我们从展开集中的每个状态生成多个轨迹，这限制了该算法的设置，系统可以重置为任意状态。相比之下，单路径算法不需要状态重置，可直接在物理系统上实现。
|
||||
|
||||
#### 5. 实用算法
|
||||
|
||||
基于单路径和vine采样方法，本文提出两种实用的策略优化算法。算法重复执行以下步骤：
|
||||
|
||||
1. 使用单路径或vine过程收集一组状态动作对，以及对应的 $Q$ 值的蒙特卡洛估计。
|
||||
|
||||
2. 通过对多个样本求平均，构造公式(15)中的估计目标和约束条件。
|
||||
|
||||
3. 近似解这个约束优化问题，更新策略的参数向量 $\theta$。本文使用共轭梯度算法，进行直线搜索。
|
||||
|
||||
|
||||
第3步，本文通过构造费雪(Fisher)信息矩阵(FIM)来解析计算KL散度的海塞(Hessian)矩阵，不用梯度的协方差矩阵。解析估计器在每个状态 $s_{n}$ 对动作进行积分，不依赖于被采样的动作 $a_{t}$。
|
||||
|
||||
总结section 3参数化策略优化与本文所提算法的联系如下:
|
||||
|
||||
* 该理论证明了用对KL散度的惩罚可以优化替代损失。然而大的惩罚系数 $\frac{2\epsilon \gamma}{({2-\gamma})^{2}}$ 会导致非常小的步长，本文算法想减小这个系数。本文采用带有参数 $\delta$ (KL散度的界)的硬约束来代替惩罚。
|
||||
|
||||
* $D^{max}_{KL}(\theta_{old},\theta)$ 的约束很难进行数值优化和估计，所以本文算法约束了 $D_{KL}(\theta_{old},\theta)$。
|
||||
|
||||
* 本文的算法理论为了简化忽略了优势函数的估计误差，但是Kakade & Langford (2002)推导中考虑了这个误差。
|
||||
|
||||
#### 6. 与以前工作的联系
|
||||
|
||||
本文推导的策略更新算法与以前的几个方法相关。
|
||||
|
||||
自然策略梯度：做为公式(13)更新的特例，通过对 $L$ 线性近似，对 $\bar{D}_{KL}$ 约束使用二次逼近，从而得到下式：
|
||||
|
||||
|
||||
|
||||
更新 $\theta _{new}=\theta _{old}-\lambda A(\theta _{old})^{-1} \nabla _{\theta }L(\theta )|_{\theta =\theta _{old}}$，其中拉格朗日乘子 $\lambda$ 为算法参数。该算法更新与本文的TRPO不同，TRPO每次更新强制执行约束。实验证明，本文算法提高了处理更大问题时的性能。
|
||||
|
||||
通过使用 $l_{2}$ 约束或惩罚，TRPO也获得了标准策略梯度更新：
|
||||
|
||||
|
||||
|
||||
通过求解无约束问题 $minimize_{\pi}L_{\pi_{old}}(\pi)$ 也可得到迭代策略更新。
|
||||
|
||||
相对熵策略搜索(REPS)约束了状态动作边缘 $p{s,a}$，然而TRPO约束了条件 $p(s,a)$，不需要在内循环中进行非线性优化。
|
||||
|
||||
Levine and Abbeel (2014)使用KL发散约束，TRPO不显式估计系统动态。
|
||||
|
||||
#### 7. 实验
|
||||
|
||||
|
||||
|
||||
图2为运动实验的二维机器人模型：swimmer，hopper，walker。由于欠驱动及接触连续，hopper和walker比较难训练。
|
||||
|
||||
实验回答了几个问题：
|
||||
|
||||
（1）单路径和vine采样的性能特点是什么？
|
||||
|
||||
（2）TRPO使用固定的KL散度对算法性能有什么影响？
|
||||
|
||||
（3）TRPO能否用于解决具有挑战性的大规模问题？当用于大规模问题时，最终性能、计算时间和样本复杂度方面，TRPO相比其他方法情况如何？
|
||||
|
||||
实验结果表明，单路径和vine算法都能从零开始训练出高质量的运动控制器，在玩Atari游戏时这些算法性能都很不错。
|
||||
|
||||
##### 7.1 模拟机械运动
|
||||
|
||||
实验：mujoco机器人移动实验（三个模拟机器人，如图2所示）
|
||||
|
||||
状态：机器人的广义位置和速度
|
||||
|
||||
控制：关节力矩
|
||||
|
||||
挑战：欠驱动，高维，接触引起的摩擦力
|
||||
|
||||
评估模型：Swimmer, Hopper, Walker，再加入一个经典的cart-pole
|
||||
|
||||
算法对模型评估的结果看图4。图3上图为机器人动作训练的网络，下图为玩Atari游戏的网络。本文用神经网络表示策略，参数见文章附录。
|
||||
|
||||
|
||||
|
||||
图4为机器人训练的学习曲线，每个算法随机初始化的五次运行平均结果，hopper和walker 的前进速度是-1，说明只学到了站立平衡，没学会如何走路。
|
||||
|
||||
|
||||
|
||||
比较的方法：单路径TRPO, vine TRPO, 奖励加权回归(RWR), 类EM的策略搜索方法，相对熵策略搜索(REPS), 交叉熵法(CEM)，无梯度法，协方差矩阵自适应(CMA), 经典自然策略梯度算法(使用固定惩罚系数-拉格朗日乘子)，经验FIM(使用梯度的协方差矩阵), max KL(只适用于cart-pole，使用最大KL散度)。
|
||||
|
||||
学习曲线显示了每种算法五次运行的平均成本，如图4所示。单路径和藤蔓TRPO解决了所有问题，得到了最好的解。自然梯度在两个较简单的问题上表现良好，但无法产生向前发展的跳跃和步行步态。这些结果提供了实验证据：与使用固定惩罚相比，约束KL散度是选择步长和取得快速、一致进步的更稳健的方法。CEM和CMA是无导数算法，因此它们的样本复杂度与参数数量成反比，在较大的问题上表现不佳。最大KL方法的学习速度比我们的最终方法要慢一些，因为约束的形式更严格，但总的来说，结果表明平均KL发散度约束与理论证明的最大KL发散度具有类似的效果。
|
||||
|
||||
TRPO学习策略的视频链接:http://sites.google.com/ site/trpopaper/。
|
||||
|
||||
##### 7.2 从图像中玩游戏
|
||||
|
||||
输入：Atari游戏原始图像
|
||||
|
||||
学习挑战：学习各种行为，延迟奖励，复杂的行为序列，变化闪烁的背景
|
||||
|
||||
做法：和DAN一样对图像预处理，两个卷积层有16个通道，stride为2，一个全连接层有20个单元，33500个参数。
|
||||
|
||||
单路径法和vine法结果如表1，还包括一个人类玩家和Deep Q-Learning,蒙特卡洛树搜索与监督训练的组合。
|
||||
|
||||
|
||||
|
||||
TRPO算法(底部行)在每个任务上运行一次，使用相同的架构和参数。性能在不同的运行之间有很大的差异(策略的随机初始化不同)，但由于时间限制，作者无法获得错误统计数据。
|
||||
|
||||
#### 8. 讨论及结论
|
||||
|
||||
本文提出并分析了随机控制策略优化的信任域方法。本文证明了TRPO的单调改进性，该算法反复优化策略的预期成本的局部近似，这个策略带有KL散度惩罚。本文表明，在一系列具有挑战性的策略学习任务中，对这个结合了KL散度的方法的近似，取得了良好的实验结果，优于以前的方法。本文的分析也为策略梯度和策略迭代方法的统一提供了一种视角，表明它们是一种算法的特殊极限情况，这种算法可以优化一个服从信任域约束的目标。
|
||||
|
||||
在机器人运动领域，本文的算法在Mujoco物理模拟器中利用神经网络和最低信息成本，成功学习了游泳、行走和跳跃的控制。在以往工作中还没有控制器使用通用策略搜索方法和非工程的通用策略表示从头学习这些任务。
|
||||
|
||||
在游戏领域，本算法使用卷积神经网络CNN，将原始图像做为输入。这需要优化极高维的策略。以前只有两种方法在此任务中获得成功。
|
||||
|
||||
#### 作者对未来的展望
|
||||
|
||||
本文的方法可扩展且具有强大的理论基础，作者希望以此为出发点，未来能训练大型的丰富的函数近似器，来解决一系列具有挑战性的问题。结合探索的两个实验的领域交叉，可以使用视觉和原始感官数据做为输入，有可能学习机器人的控制策略，为训练结合感知和控制的机器人控制器提供一个统一方案。可以使用更为复杂的策略，包括带有隐藏状态的循环策略，可以进一步使状态估计和控制在部分可观测的设置中滚动到相同的策略。通过将本文的方法与模型学习相结合，也有可能大幅降低样本复杂度，使其适用于样本珍贵的现实环境。
|
||||
|
||||
#### 个人理解
|
||||
|
||||
使用值函数解决连续状态空间问题，选择动作的策略通常是不变的确定性策略。有些实际问题需要的最优策略并不是确定性的，而是随机策略，策略梯度就是解决产生随机策略的问题。经典的蒙特卡罗策略梯度方法基于采样的方法，给定策略 $\pi$, 让智能体与环境互动，会得到很多条轨迹，每条轨迹都有对应的回报。将每条轨迹回报进行平均，就可以知道某一个策略下面状态的价值。在PG算法中，因为策略是一个概率，不能直接用来迭代，所以将策略转化为函数形式。使用带有参数 $\theta$ 的函数对策略进行近似，通过更新 $\theta$ 逼近最优策略。本人的研究内容并不是RL算法本身，只是考虑应用策略梯度算法，没有做过相关的项目，因此对本文理解尚浅，欢迎交流讨论。
|
||||
|
||||
汪莉娟：天津大学研究生，专业方向为控制科学与工程，主要研究方向为交通优化与智能控制。
|
||||
|
||||
BIN
papers/Policy_gradient/img/ACKTR-1-1.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-1-1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 4.9 KiB |
BIN
papers/Policy_gradient/img/ACKTR-1-2.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-1-2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 6.2 KiB |
BIN
papers/Policy_gradient/img/ACKTR-1-3.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-1-3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 118 KiB |
BIN
papers/Policy_gradient/img/ACKTR-1.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 106 KiB |
BIN
papers/Policy_gradient/img/ACKTR-2-1.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-2-1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 4.8 KiB |
BIN
papers/Policy_gradient/img/ACKTR-2-2.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-2-2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 64 KiB |
BIN
papers/Policy_gradient/img/ACKTR-2-3.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-2-3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 90 KiB |
BIN
papers/Policy_gradient/img/ACKTR-2-4.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-2-4.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 91 KiB |
BIN
papers/Policy_gradient/img/ACKTR-2-5.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-2-5.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 40 KiB |
BIN
papers/Policy_gradient/img/ACKTR-2.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 47 KiB |
BIN
papers/Policy_gradient/img/ACKTR-3-1.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-3-1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 34 KiB |
BIN
papers/Policy_gradient/img/ACKTR-3.png
Normal file
BIN
papers/Policy_gradient/img/ACKTR-3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 64 KiB |
BIN
papers/Policy_gradient/img/C51_1.png
Normal file
BIN
papers/Policy_gradient/img/C51_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 69 KiB |
BIN
papers/Policy_gradient/img/C51_2.png
Normal file
BIN
papers/Policy_gradient/img/C51_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 69 KiB |
BIN
papers/Policy_gradient/img/C51_3.png
Normal file
BIN
papers/Policy_gradient/img/C51_3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 82 KiB |
BIN
papers/Policy_gradient/img/C51_4.png
Normal file
BIN
papers/Policy_gradient/img/C51_4.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 231 KiB |
BIN
papers/Policy_gradient/img/C51_5.png
Normal file
BIN
papers/Policy_gradient/img/C51_5.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 72 KiB |
BIN
papers/Policy_gradient/img/C51_6.png
Normal file
BIN
papers/Policy_gradient/img/C51_6.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 80 KiB |
BIN
papers/Policy_gradient/img/DPG_1.png
Normal file
BIN
papers/Policy_gradient/img/DPG_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 68 KiB |
BIN
papers/Policy_gradient/img/DPG_2.png
Normal file
BIN
papers/Policy_gradient/img/DPG_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 134 KiB |
BIN
papers/Policy_gradient/img/DPG_3.png
Normal file
BIN
papers/Policy_gradient/img/DPG_3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 72 KiB |
BIN
papers/Policy_gradient/img/GAE_1.png
Normal file
BIN
papers/Policy_gradient/img/GAE_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 57 KiB |
BIN
papers/Policy_gradient/img/GAE_2.png
Normal file
BIN
papers/Policy_gradient/img/GAE_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 278 KiB |
BIN
papers/Policy_gradient/img/GAE_3.png
Normal file
BIN
papers/Policy_gradient/img/GAE_3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 134 KiB |
BIN
papers/Policy_gradient/img/PPO_1.png
Normal file
BIN
papers/Policy_gradient/img/PPO_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 72 KiB |
BIN
papers/Policy_gradient/img/PPO_2.png
Normal file
BIN
papers/Policy_gradient/img/PPO_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 23 KiB |
BIN
papers/Policy_gradient/img/PPO_3.png
Normal file
BIN
papers/Policy_gradient/img/PPO_3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 30 KiB |
BIN
papers/Policy_gradient/img/PPO_4.png
Normal file
BIN
papers/Policy_gradient/img/PPO_4.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 35 KiB |
BIN
papers/Policy_gradient/img/PPO_5.png
Normal file
BIN
papers/Policy_gradient/img/PPO_5.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 153 KiB |
BIN
papers/Policy_gradient/img/SAC_1.png
Normal file
BIN
papers/Policy_gradient/img/SAC_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 84 KiB |
BIN
papers/Policy_gradient/img/SAC_2.png
Normal file
BIN
papers/Policy_gradient/img/SAC_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 465 KiB |
BIN
papers/Policy_gradient/img/SAC_3.png
Normal file
BIN
papers/Policy_gradient/img/SAC_3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 65 KiB |
BIN
papers/Policy_gradient/img/SAC_4.png
Normal file
BIN
papers/Policy_gradient/img/SAC_4.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 444 KiB |
BIN
papers/Policy_gradient/img/TD_1.png
Normal file
BIN
papers/Policy_gradient/img/TD_1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 117 KiB |
BIN
papers/Policy_gradient/img/TD_2.png
Normal file
BIN
papers/Policy_gradient/img/TD_2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 28 KiB |
BIN
papers/Policy_gradient/img/TRPO--0.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--0.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 17 KiB |
BIN
papers/Policy_gradient/img/TRPO--1.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 11 KiB |
BIN
papers/Policy_gradient/img/TRPO--10.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--10.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 6.7 KiB |
BIN
papers/Policy_gradient/img/TRPO--11.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--11.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 12 KiB |
BIN
papers/Policy_gradient/img/TRPO--12.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--12.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 6.7 KiB |
BIN
papers/Policy_gradient/img/TRPO--13.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--13.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 6.9 KiB |
BIN
papers/Policy_gradient/img/TRPO--14.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--14.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 7.2 KiB |
BIN
papers/Policy_gradient/img/TRPO--15.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--15.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 11 KiB |
BIN
papers/Policy_gradient/img/TRPO--16.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--16.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 5.3 KiB |
BIN
papers/Policy_gradient/img/TRPO--17.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--17.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 9.0 KiB |
BIN
papers/Policy_gradient/img/TRPO--18.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--18.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 19 KiB |
BIN
papers/Policy_gradient/img/TRPO--2.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--2.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 5.8 KiB |
BIN
papers/Policy_gradient/img/TRPO--3.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--3.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 5.6 KiB |
BIN
papers/Policy_gradient/img/TRPO--4.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--4.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 6.4 KiB |
BIN
papers/Policy_gradient/img/TRPO--5.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--5.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 2.9 KiB |
BIN
papers/Policy_gradient/img/TRPO--8.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--8.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 22 KiB |
BIN
papers/Policy_gradient/img/TRPO--9.png
Normal file
BIN
papers/Policy_gradient/img/TRPO--9.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 5.1 KiB |
BIN
papers/Policy_gradient/img/TRPO-0.png
Normal file
BIN
papers/Policy_gradient/img/TRPO-0.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 9.3 KiB |
BIN
papers/Policy_gradient/img/TRPO-1.png
Normal file
BIN
papers/Policy_gradient/img/TRPO-1.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 61 KiB |
BIN
papers/Policy_gradient/img/TRPO-11.png
Normal file
BIN
papers/Policy_gradient/img/TRPO-11.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 26 KiB |
BIN
papers/Policy_gradient/img/TRPO-12.png
Normal file
BIN
papers/Policy_gradient/img/TRPO-12.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 5.4 KiB |
BIN
papers/Policy_gradient/img/TRPO-13.png
Normal file
BIN
papers/Policy_gradient/img/TRPO-13.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 4.6 KiB |
BIN
papers/Policy_gradient/img/TRPO-14.png
Normal file
BIN
papers/Policy_gradient/img/TRPO-14.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 9.6 KiB |
BIN
papers/Policy_gradient/img/TRPO-19.png
Normal file
BIN
papers/Policy_gradient/img/TRPO-19.png
Normal file
Binary file not shown.
|
After Width: | Height: | Size: 8.5 KiB |
Some files were not shown because too many files have changed in this diff Show More
Reference in New Issue
Block a user