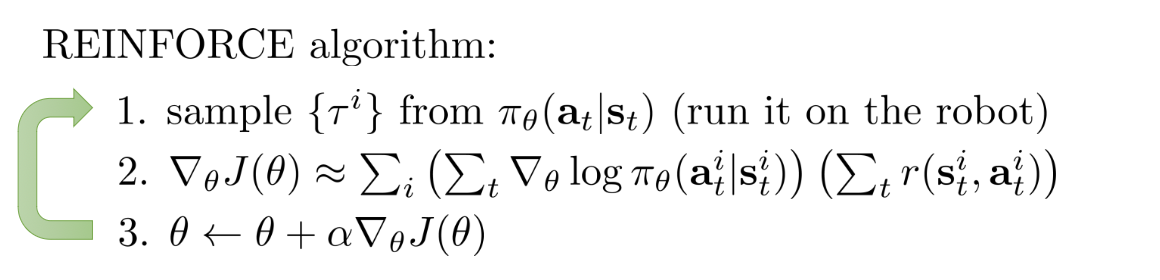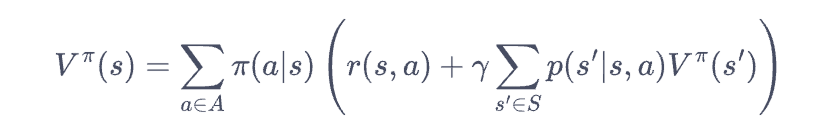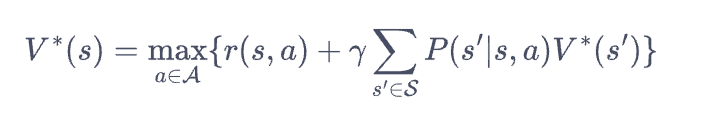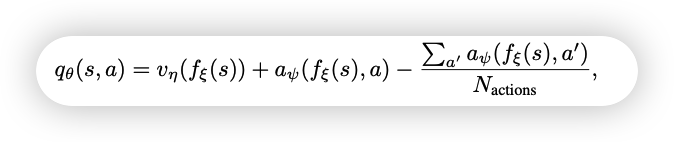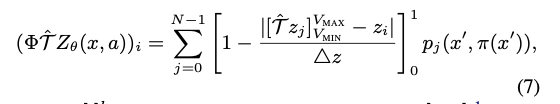17 KiB
JOYRL论文阅读<Rainbow: Combining Improvements in Deep Reinforcement Learning>
作者:Hessel, M., Modayil, J., Van Hasselt, H., Schaul, T., Ostrovski, G., Dabney, W., ... & Silver, D.
实验室:Google DeepMind
论文地址:https://arxiv.org/pdf/1710.02298
发表: In Thirty-second AAAI conference on artificial intelligence.
1 摘要
1.1 摘要--背景及问题
从DQN1推导过程中发现依旧存在很多问题,常见的改进措施Double DQN2、Dueling DQN3、Prioritized replay4、Multi-step5、Distributional RL6、Noisy Net7等方法,这些方法并不是完全独立,比如在Dueling中其实已经将Double DQN和Prioritized replay结合起来。
1.2 摘要--方法
本文希望将上述六种DQN方法结合经验融合在一起,来得到一个更好的网络。
1.3 摘要--贡献
- 成为Atari 2600中SOTA(State-of-the-art)
- 我们还提供详细的消融研究的结果,该研究结果显示了每个组件对整体性能的贡献。
2 问题背景
2.1 RL problem & 记号
强化学习希望一个具有动作(Action)的智能体(Agent) 在与环境(Environment)交互的过程可以最大化奖励(Reward),在这个过程中并不会直接监督式的学习。这里分享另外一种定义:
一、Mathematical formalism for learning- based decision making
二、Approach for learning decision-making and control from experience
**MDP (Markov Decision Process) \{S,A,T,r,\gamma\} **
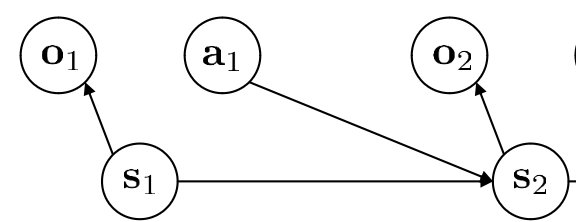
在不同的时间步下$t=0,1,2,..$,环境状态$S_t$提供给智能体一个观测信息$O_t$,通常我们会认为是完全观测(即S_t=O_t),同时智能体根据观测信息做出动作$A_t$,之后环境给出下一个奖励$R_{t+1}$,奖励的折扣$\gamma_{t+1}$以及更新状态为S_{t+1}
在这个过程通常$S,A$是有限的情况,对于环境来说状态转移 (Stochastic transition function)、奖励方程包括
T(s,a,s')=P[S_{t+1=s'}|S_t=s,A_t=a]
r(s,a)=E[R_{t+1}|S_t=s,A_t=a]
对于智能体来说,根据状态$S_t$(或者完全观测下的观测O_t)得到得到动作$A_t$来自于策略$\pi$(Policy),在序列决策中我们的目标是最大化某个状态采取某个动作的折扣奖励之和
P(A_t=a)=\pi_{\theta}[A_t=a|S_t=s]
max G_t=\Sigma_{k=0}^{\infty}r_t^{k}R_{t+k+1}
我们在利用算法进行梯度提升通常会经过三个步骤:
- 生成样本
- 评估模型或者是计算回报
- 提升策略
2.2 Policy Gradient:直接提升策略
为了最大化策略的回报,我们可以直接对$G_t$最大化(即REINFRORCEMENT算法)
我们可以利用Baseline、N-steps、Discount、Importance sampling等技巧对算法进行改进。
2.3 Actor-Crtic方法:评估汇报(Estimate return)与提升策略分开
也可以引入新的状态价值函数$V^{\pi}(s)$来结合拟合的方式计算$G_t$之后最大化(A3C),也可以直接利用 $V^{\pi}(s)$和动作状态价值函数$Q^{\pi}(s,a)$来进行基于价值函数的学习方法。
V^{\pi}(s)=E_{\pi}[G_t|S_t=s]
Q^{\pi}(s,a)=E_\pi[G_t|S_t=s,A_t=a]
我们可以利用回放池(Replay buffer)、神经网络来学习降低策略梯度中的方差。
2.4 Value-based method 抛弃策略
Policy iteration->Value iteration->Q learning
首先从策略迭代与价值迭代说起,参考链接可以看作是利用动态规划的方式反应强化学习的过程,两者的区别在于反应的是贝尔曼期望还是贝尔曼最优。
在基于价值学习算法的过程中,优点是我们只需要一个经验回放池,只需要$(s,a,s',r)$而不是需要完整的决策序列。我们通常会引入随机探索(Exploration)的概念,常见的包括$\epsilon-Greedy$的方法,在一定概率下选择非策略产生的动作。
在价值迭代的基础上,我们可以抛弃对$V(s)$的学习,而只是记录Q(s,a); Q-iteration algorithm (或者Q-learning)的过程如下图所示
2.5 DQN推导
在上述我们认识对于MDP目标,从显式表达策略,到结合状态价值再到之后的完全使用价值函数来使用学习的方法,我们仍然没有解决的问题包括
- 状态-动作空间的连续性
- 在状态空间和动作空间纬度大的时候无法准确刻画 状态-动作价值
随着神经网络的发展,我们希望利用网络拟合的方式来解决上述问题,同时每一步利用$\epsilon-Greedy$的方式来探索回放池中的经验,并利用梯度下降等方法最小化价值函数表达的回报
min (R_{t+1}+\gamma_{t+1}max_{a'}(S_{t+1},a')-q_{\theta}(S_t,A_t))^2
- 1 初始化大小为$N$的经验回放池 (PS:注意有大小限制)
- 2 用相同随机的网络参数初始化
Q_{\theta}(s,a)与目标网络Q_{\theta'}(s,a) - 3 FOR 回合 = 1,N DO:
- 4 获取环境初始状态
s_1 - 5 FOR 时间步 = 1,T DO:
- 6 根据当前网络$a_t=max_a Q_{\theta}(s,a)$结合$\epsilon-Greedy$方法来得到$a_t$(PS:注意这一步动作的确定隐含之后DQN回报偏大的特点)
- 7 执行动作
a_t,获取r_t,环境状态变为s_{t+1} - 8 存储上述采样信息到经验回放池
- 9 if 经验回放池数目足够:
- 10 采样batchsize个样本
\{s_t^i,a_t^i,r_t^i,s_{t+1}^i\} - 11 计算目标值
y^i_t=r^i_t+\gamma*max_aQ_{\hat \theta}(s^i_{t+1},a^i_t) - 12 最小化损失函数
L=\frac{1}{N}(y_t^i-Q_{\theta}(s_t^i,a_t^i))^2 - 13 更新网络参数
- 10 采样batchsize个样本
- 14 END FOR
- 15 更新目标网络参数
- 4 获取环境初始状态
- 16 END FOR
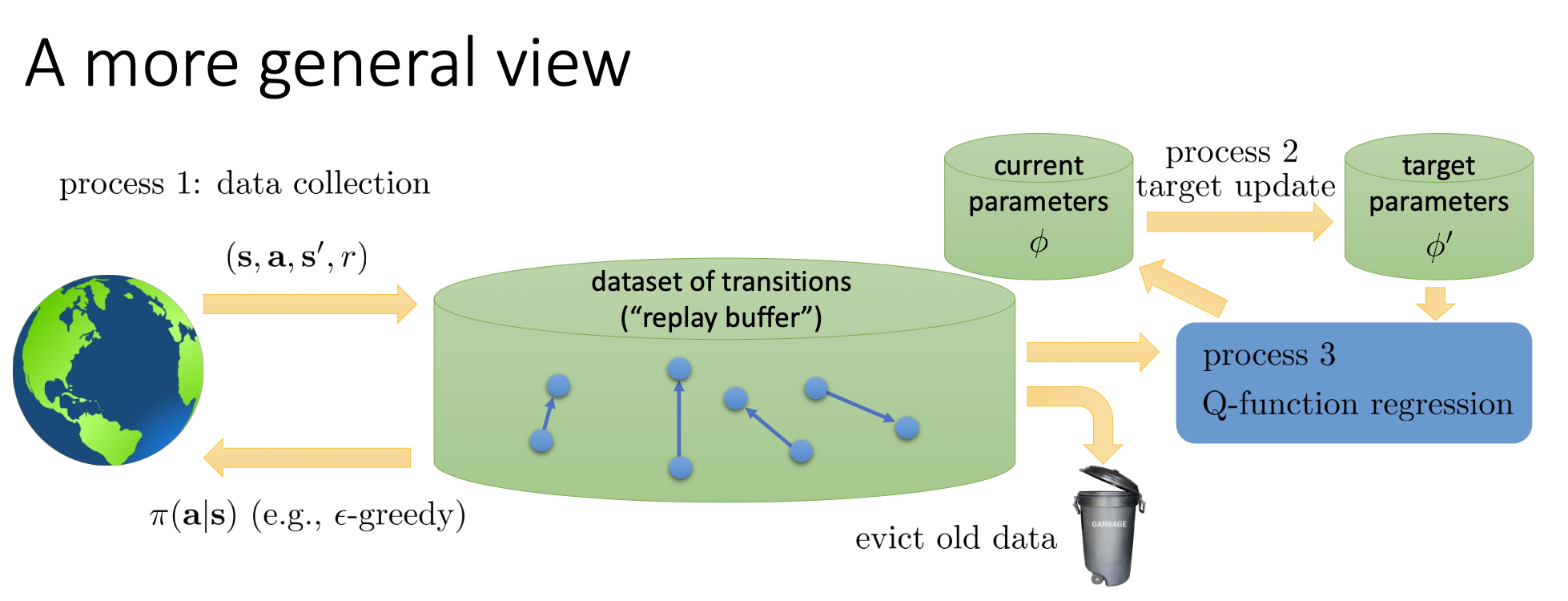
其中非常有趣的技巧包括:
- 经验回放(Experience replay)与随机探索;这一部分主要是为了提高样本采样效率,同时降低后续梯度下降中样本的相关性。
- 目标网络(Target network);由于TD误差在策略改变过程中也会改变,因此造成神经网络拟合过程的不稳定性,因此构建新的目标网络,在每次迭代过程中暂时固定,在回合结合后更新参数,这样需要两层Q网络。
3 DQN改进
虽然DQN成功让强化学习在某些方面超过人类,但是依旧有这许多限制。
3.1 改进1:Double Q- Learning
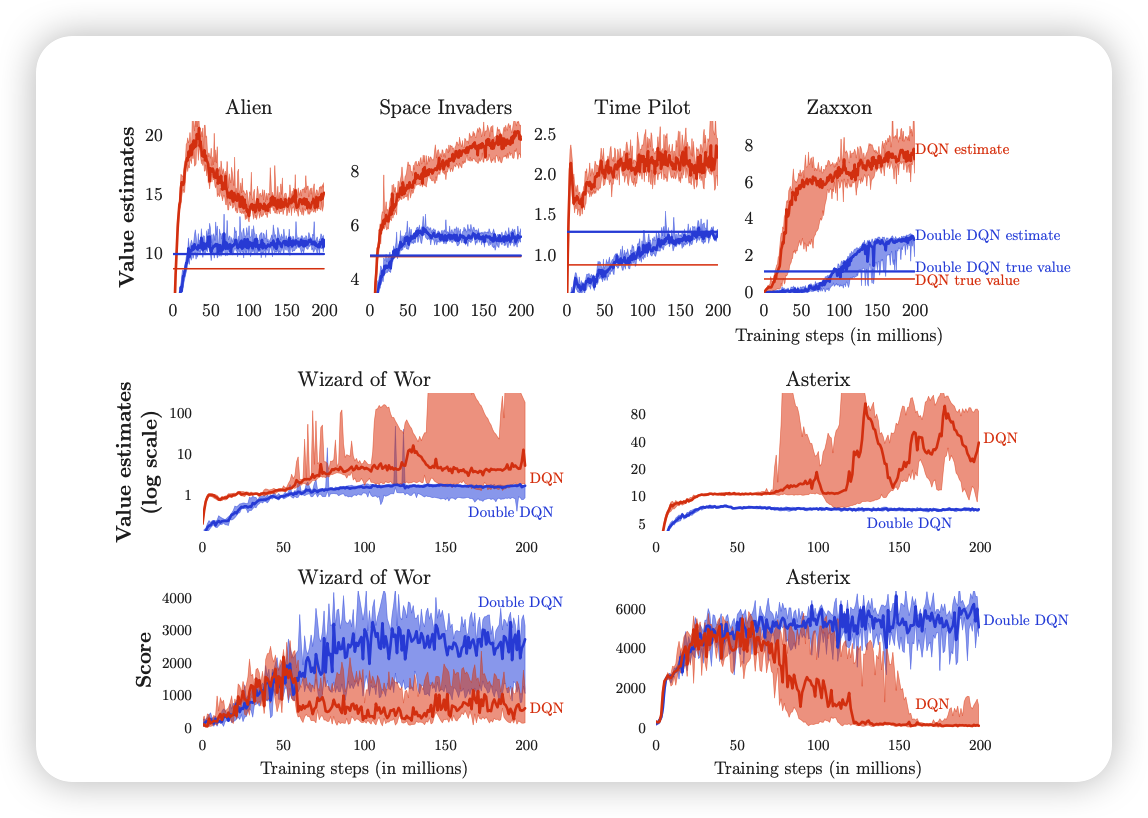
在DQN中会有估计值过高的情况,证明如下:
target-value:y^i_t=r^i_t+\gamma max_{a_{t+1}^i}Q_{\hat \theta}(S^i_{t+1},a^i_{t+1})
max_{a_{t+1}^i}Q_{\hat \theta}(S^i_{t+1},a^i_{t+1})=Q_{\hat \theta}(s_{t+1}^i,argmax_{a_{t+1}^i}Q_{\hat \theta}(s_{t+1}^i,a_{t+1}^i))
根据期望公式
E[max(X1,X2)]>max(E(X1),E(X2))
我们通过证明发现估计值较大的原因是因为我在模型选择行为和计算Q值使用同一个网络,如果降低行为选择和Q值计算的相关性就可以降低高估,因此直觉的我们可以设计两个网络
Q_{\theta_A}(s,a)=r+\gamma Q_{\theta_b}(s',a')
Q_{\theta_B}(s,a)=r+\gamma Q_{\theta_a}(s',a')
我们的确可以新加一个网络,但是会增加学习难度,需要重新设计架构。所以为什么不直接使用$Q_{\theta}(s,a)$作为行为的估计?
(target\_value\_double\_Q-learning):y^i_t=r^i_t+\gamma Q_{\hat \theta}(s^i_{t+1},argmax_{r^i_{t+1}Q_{\theta}}(s^i_{t+1},a^i_{t+1}))
3.2 改进2:Prioritized replay
在DQN学习中为高效利用$(s,a,r,s)$样本,我们会使用经验回放的方式来存储一定规模的样本,在梯度下降的时候通常是从经验回放中均匀采样(Uniformly sampling)来进行学习,但是我们依旧会存在两个问题:
- 依旧没有完全解决数据之间独立同分布的假设
- 容易忘记一些罕见的、重要的经验数据
在该论文中作者首先制定指标“TD-error”作为衡量$(s_t^i,a_t^i,r_t^i,s^i_{t+1})$的信息量大小,作为采样的优先级,同时利用随机优先级采样、偏置和重要性采样等方式来避免贪心的问题。优先级的获取有3.2.1和3.2.2两种方式
(随机采样)P(i)=\frac{p_i^\alpha}{\Sigma_kP_k^\alpha}
3.2.1 比例优先级(Proportional prioritization)
P_i=|\sigma_i|+\epsilon
3.2.2 基于排名的优先级(Rank-based prioritization)
$P_i=\frac{1}{rank(i)}$;优点可以保证线性性质,对异常值不敏感。
上述两种是不同得到重要性的方式;在实现时候采用Sum-tree的数据结构降低算法复杂程度。在采样中考虑重要性采样(Importance sampling),并由此来进行热偏置(Annealing the bias)来修正误差
w_j=(\frac{1}{N}*\frac{1}{P(i)})^\beta
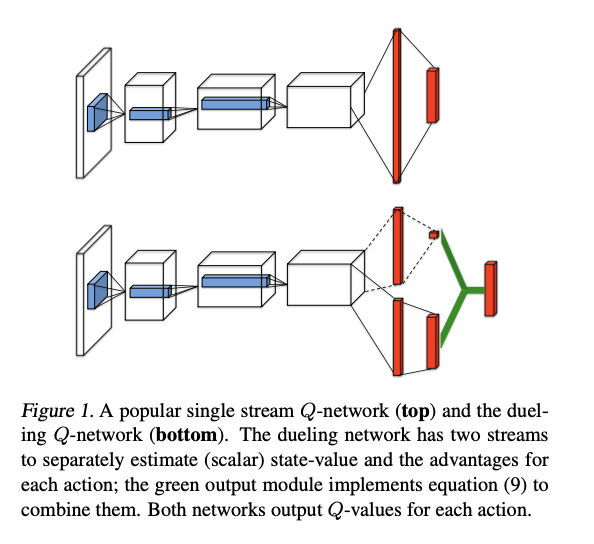
3.3 改进3:Dueling networks
Dueling DQN是一种针对基于价值函数的强化学习的网络结构设计,其并不直接输出状态动作价值函数,而是输出状态价值函数与动作状态优势函数,因为通常会共用前几层的卷积参数,在后面则是状态价值函数与优势函数各自的参数。
3.4 改进4:Multi-step learning
在对状态动作函数的优势估计时候,通常我们会分为蒙特卡洛方法与Bootstrap(或者是Actor- critic内的C)的方法
(MC-sampling)A_t=\Sigma_{k=0}^{\infty}\gamma_t^{k}(R_{t+k+1}-b)
(bootstrap-sampling)G_t=r_{t}+\gamma*V(s_{t+1})-V(s_t)
前者方法偏差低但是方差较大;后者方差低但是有偏。因此结合两者我们通常会有Multi-step target的方法。
同样的也可以用在DQN中对于状态动作价值函数的估计:
R_t^{n}=\Sigma_{k=0}^{n-1}\gamma_t^{k}R_{t+k+1}
更新之后的损失函数为
(R_t^{n}+\gamma_t^nmax_{a'}Q_{\hat \theta}(S_{t+n},a')-Q_\theta(S_t,A_t))^2
3.5 改进5:Distributional RL
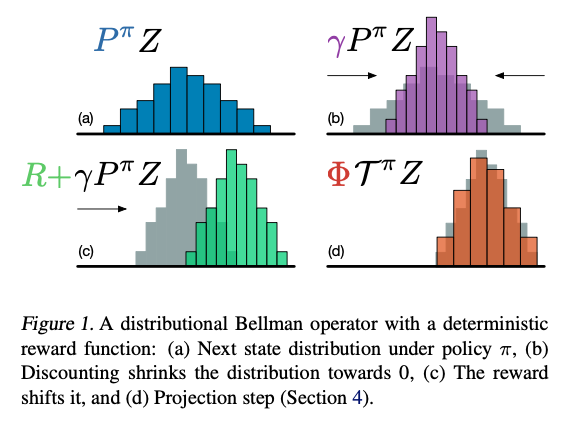
在基于价值函数的学习中我们通常是返回一个期望或者最大值而丢失很多其他信息,因此Distributional RL尝试利用其分布而不是单个值来进行强化学习。首先本文尝试将价值函数范围$[V_{min},V_{max}]$划分为N个各自来估计价值函数,利用Boltzmann分布表示价值函数的分布,同时利用投影的操作
由此对于分布拟合可以划分为交叉熵的形式,算法流程
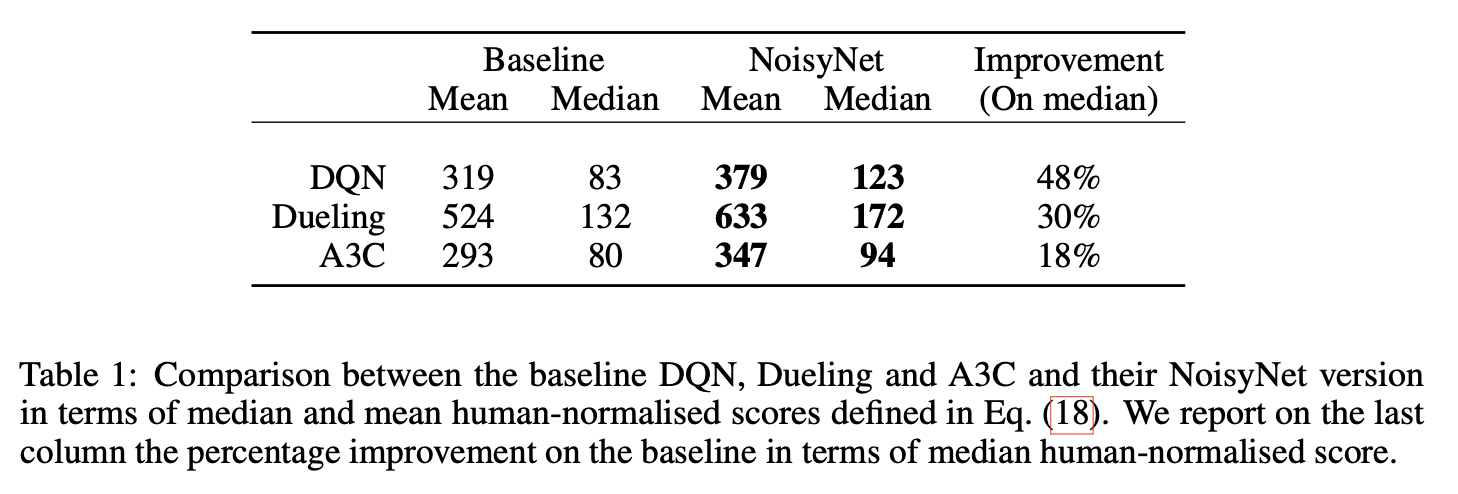
3.6 改进6:Noisy Nets
在Q- learning或者是DQN中,我们的轨迹并不是完全采样的,而是与我们的探索策略相关,最原本的是$\epsilon-Greedy$策略,这里提出一种NoisyNet来对参数增加噪声来增加模型的探索能力
y=(Wx+b)+(b_{noisy}\odot\epsilon^b+W_{noisy}\odot\epsilon^w)x
噪声的生成可以分为Independent Gaussian noise;Factorised Gaussian noise两种方式。
3.7 融合上述策略
首先将(改进5:Distributional RL)中的损失函数更换称为(改进4:Multi-step learning),并利用(改进1--Double Q- Learning)计算新的目标值
d_t^n=(R_t^n+r_t^nz,p_\hat\theta(S_{t+n},a^*_{t+n}))
损失函数为
D_{KL}(\Phi_zd_t^n||d_t)
同时在采样过程中我们通常会减少TD-error,而在本文中我们的损失函数为KL损失,因此我们的(改进2:Prioritized replay)中的优先级定义为
p_t\propto (D_{KL}(\Phi_zd_t^n||d_t))^w
同时改变(改进3: Dueling networks)由接受期望转向接受价值函数分布,最后更改所有的线性层更换为(改进6:Noisy Nets)
p_\theta(s,a)^i=\frac{exp(v^i_\eta(\phi)+a^i_\psi(\phi,a)-\hat a_\psi^i(s))}{\Sigma_j exp(v^j_\eta(\phi)+a^j_\psi(\phi,a)-\hat a_\psi^j(s)) }
4 实验
5 总结
5.1 结论
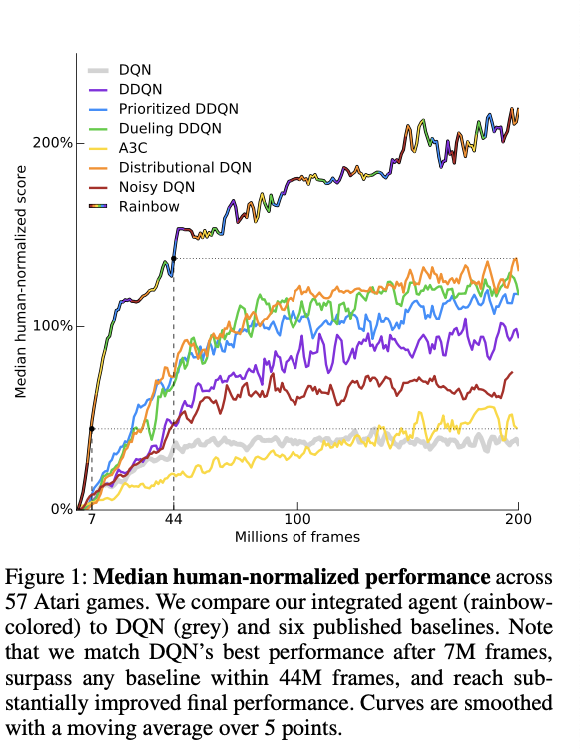
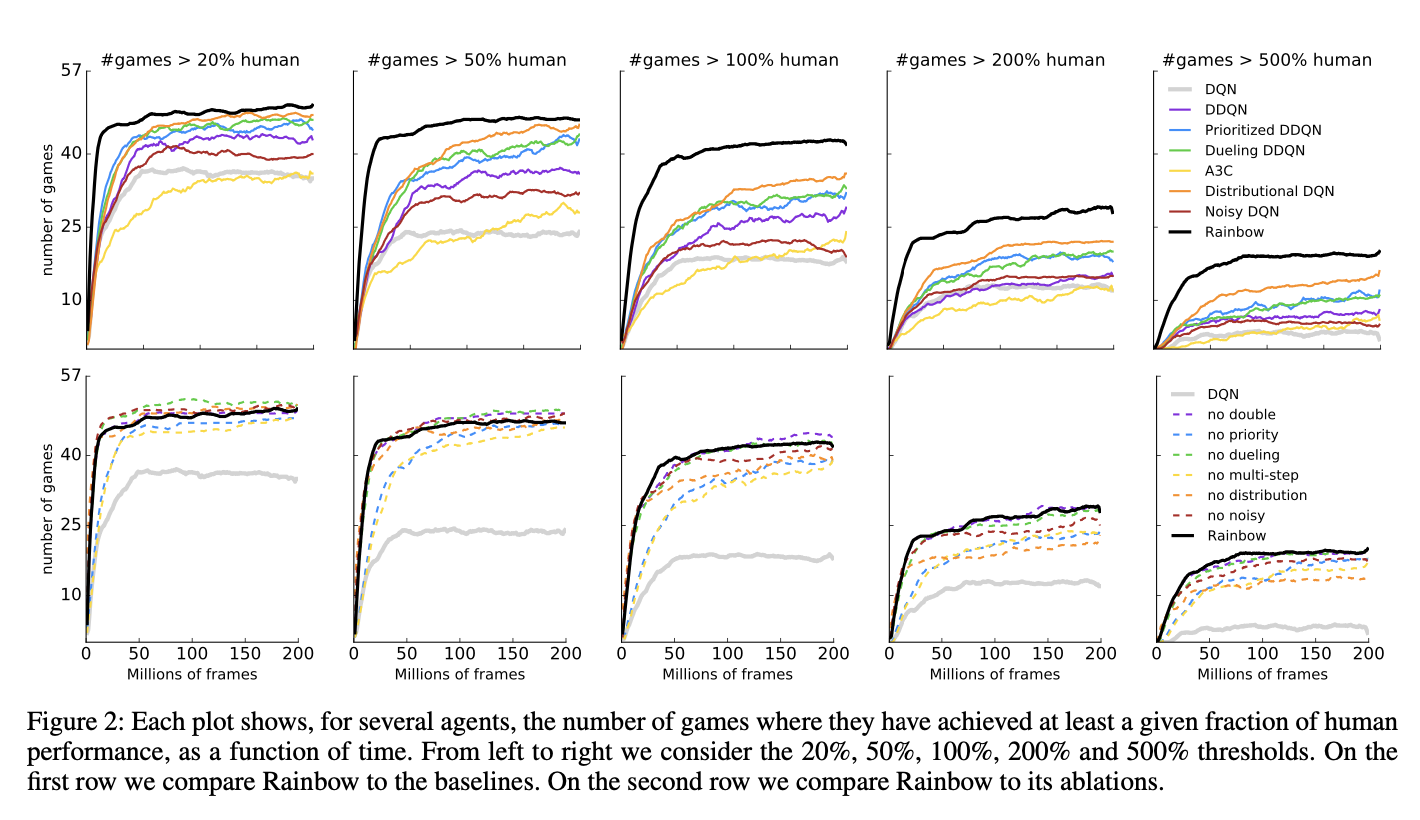
- Rainbow相比较其他现有的算法要更好,速度也会更快
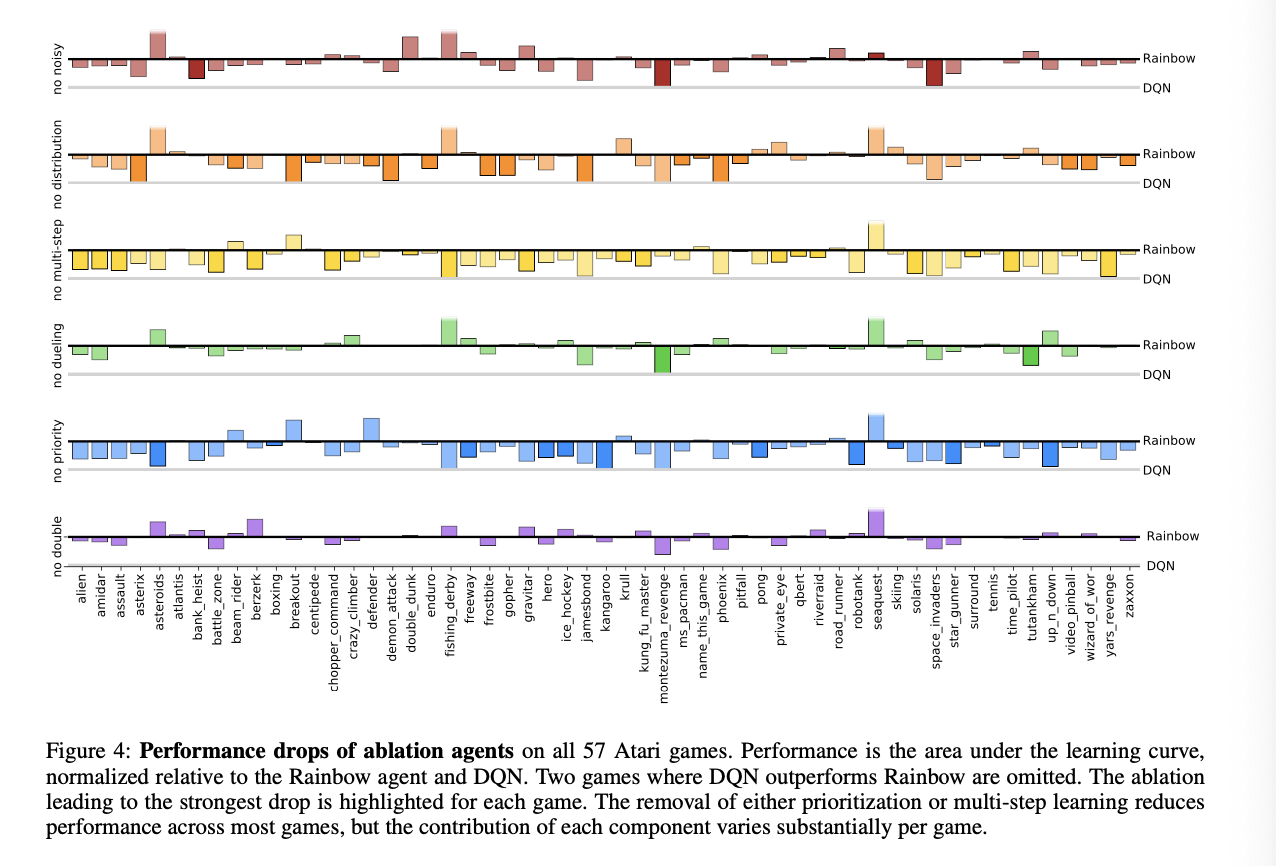
- 在消融实验中;我们会发现(改进2:Prioritized replay)与(改进4:Multi-step learning)会造成结果中位数大幅度下降;(改进5:Distributional RL)在最开始表现良好,但是最终结果表现较差;同时(改进6:Noisy Nets)通常会有更好的中位数表现,同时由于本次状态中通常是underestimate的,所以(改进1--Double Q- Learning)效果并不显著,(改进3: Dueling networks)提升幅度不大。
5.2 讨论
作者在最后总结他们的工作,主要是从Value- based的Q-learning方法集合中寻找,而没有考虑Purely policy- based的算法(比如TRPO),本文从网络探索、网络初始化、数据使用、损失或函数等方面进行集合,与之相对应的同样有很多工作,未来还可以用很多其他的方法。但是
In general, we believe that exposing the real game to the agent is a promising direction for future research.
5.3 个人感悟
这篇论文的观点很直接,在实际实现的过程中作者做了很多Dirty work,尝试过很多次,并最终证明集成的方式是有效的,以及分析哪些技巧是有效的、哪些技巧是欠佳的,工作量非常大!
自我介绍
非典型INFJ,一枚普通985的交通信息方向2022级硕士生,主要研究方向为交通数据分析、组合优化等,在学习的路上希望自己可以保持“求知若饥,虚心若愚”。可以在blog.tjdata.site找到我。