24 KiB
Actor-Critic
Actor-Critic
在 REINFORCE 算法中,每次需要根据一个策略采集一条完整的轨迹,并计算这条轨迹上的回报。这种采样方式的方差比较大,学习效率也比较低。我们可以借鉴时序差分学习的思想,使用动态规划方法来提高采样的效率,即从状态 s 开始的总回报可以通过当前动作的即时奖励 r(s,a,s') 和下一个状态 s' 的值函数来近似估计。
演员-评论家算法(Actor-Critic Algorithm)是一种结合策略梯度和时序差分学习的强化学习方法,其中:
- 演员(Actor)是指策略函数 $\pi_{\theta}(a|s)$,即学习一个策略来得到尽量高的回报。
- 评论家(Critic)是指值函数 $V^{\pi}(s)$,对当前策略的值函数进行估计,即评估演员的好坏。
- 借助于值函数,演员-评论家算法可以进行单步更新参数,不需要等到回合结束才进行更新。
在 Actor-Critic 算法 里面,最知名的方法就是 A3C(Asynchronous Advantage Actor-Critic)。
- 如果去掉 Asynchronous,只有
Advantage Actor-Critic,就叫做A2C。 - 如果加了 Asynchronous,变成
Asynchronous Advantage Actor-Critic,就变成A3C。
Review: Policy Gradient
那我们复习一下 policy gradient,在 policy gradient,我们在更新 policy 的参数 \theta 的时候,我们是用了下面这个式子来算出 gradient。
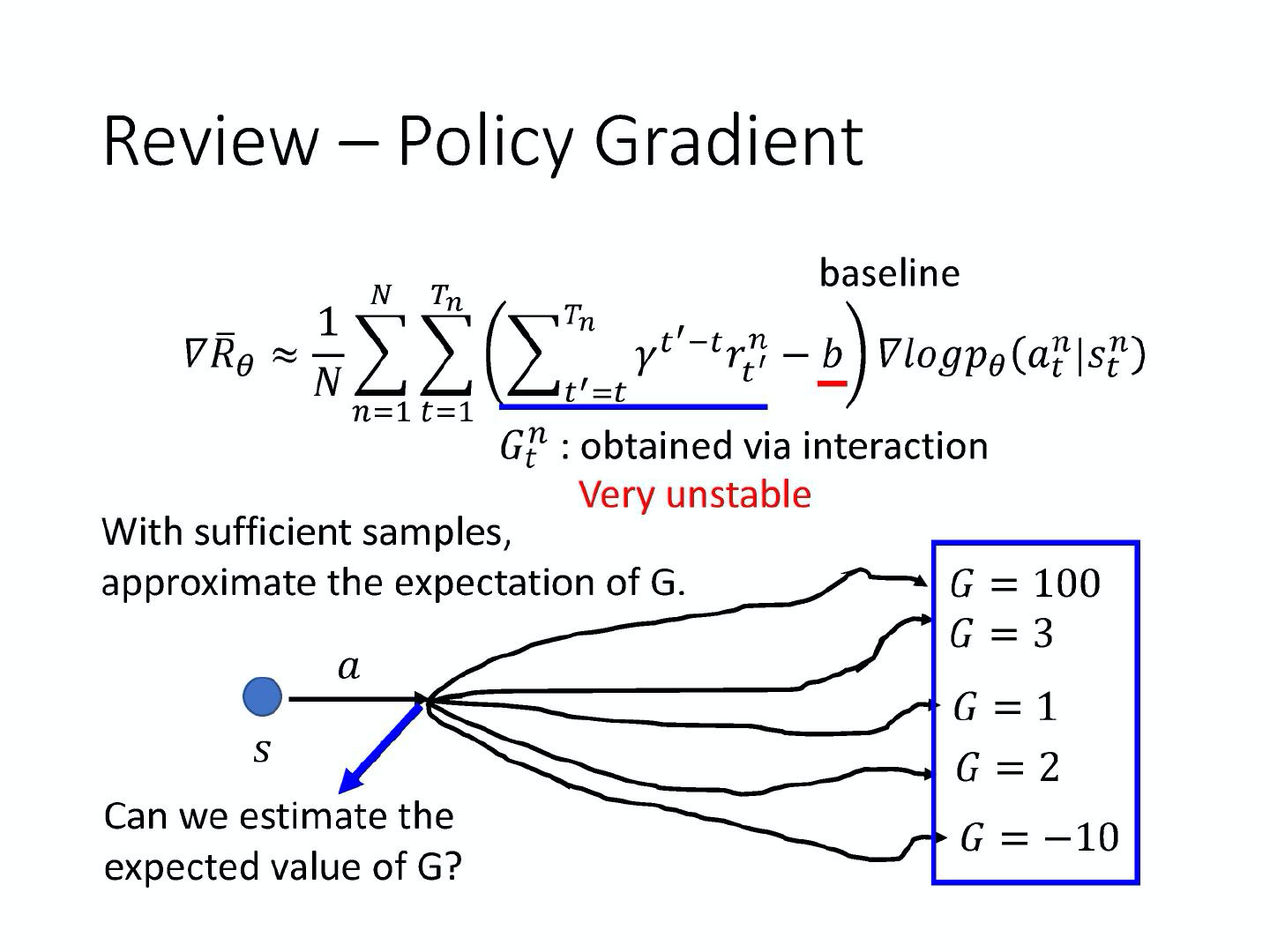
\nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}}\left(\sum_{t^{\prime}=t}^{T_{n}} \gamma^{t^{\prime}-t} r_{t^{\prime}}^{n}-b\right) \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right)
这个式子是在说,我们先让 agent 去跟环境互动一下,那我们可以计算出在某一个状态 s,采取了某一个动作 a 的概率 $p_{\theta}(a_t|s_t)$。接下来,我们去计算在某一个状态 s 采取了某一个动作 a 之后,到游戏结束为止,累积奖励有多大。我们把这些奖励从时间 t 到时间 T 的奖励通通加起来,并且会在前面乘一个折扣因子,可能设 0.9 或 0.99。我们会减掉一个 baseline b,减掉这个值 b 的目的,是希望括号这里面这一项是有正有负的。如果括号里面这一项是正的,我们就要增加在这个状态采取这个动作的机率;如果括号里面是负的,我们就要减少在这个状态采取这个动作的机率。
我们把用 G 来表示累积奖励。但 G 这个值,其实是非常不稳定的。因为互动的过程本身是有随机性的,所以在某一个状态 s 采取某一个动作 a,然后计算累积奖励,每次算出来的结果都是不一样的,所以 G 其实是一个随机变量。给同样的状态 s,给同样的动作 a,G 可能有一个固定的分布。但我们是采取采样的方式,我们在某一个状态 s 采取某一个动作 a,然后玩到底,我们看看得到多少的奖励,我们就把这个东西当作 G。
把 G 想成是一个随机变量的话,我们实际上是对这个 G 做一些采样,然后拿这些采样的结果,去更新我们的参数。但实际上在某一个状态 s 采取某一个动作 a,接下来会发生什么事,它本身是有随机性的。虽然说有个固定的分布,但它本身是有随机性的,而这个随机变量的方差可能会非常大。你在同一个状态采取同一个动作,你最后得到的结果可能会是天差地远的。
假设我们可以采样足够的次数,在每次更新参数之前,我们都可以采样足够的次数,那其实没有什么问题。但问题就是我们每次做 policy gradient,每次更新参数之前都要做一些采样,这个采样的次数其实是不可能太多的,我们只能够做非常少量的采样。如果你正好采样到差的结果,比如说你采样到 G = 100,采样到 G = -10,那显然你的结果会是很差的。
Review: Q-learning
Q: 能不能让整个训练过程变得比较稳定一点,能不能够直接估测 G 这个随机变量的期望值?
A: 我们在状态 s 采取动作 a 的时候,直接用一个网络去估测在状态 s 采取动作 a 的时候,G 的期望值。如果这件事情是可行的,那之后训练的时候,就用期望值来代替采样的值,这样会让训练变得比较稳定。
Q: 怎么拿期望值代替采样的值呢?
A: 这边就需要引入基于价值的(value-based)的方法。基于价值的方法就是 Q-learning。Q-learning 有两种函数,有两种 critics。
-
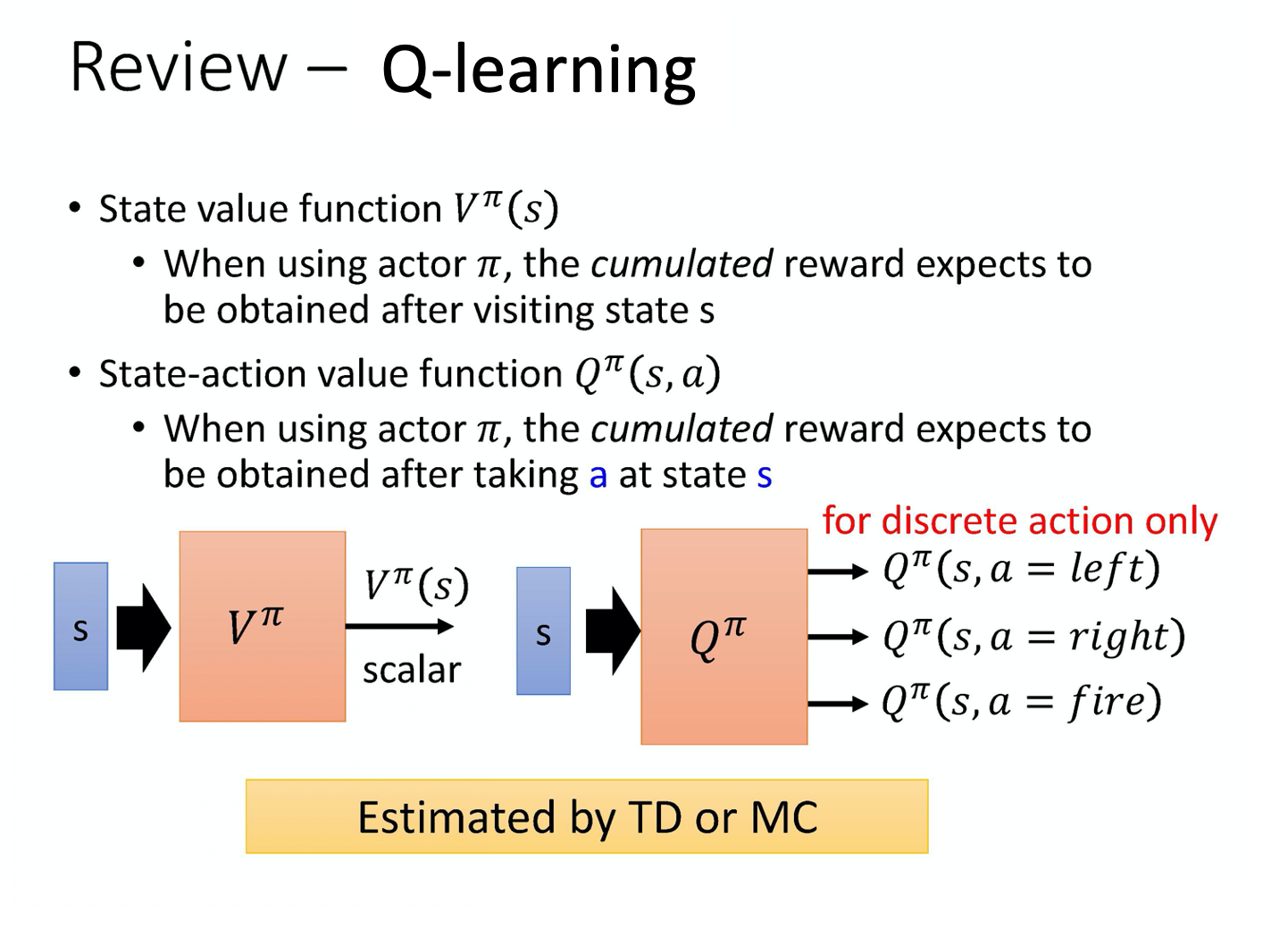
第一种 critic 是 $V^{\pi}(s)$,它的意思是说,假设 actor 是 $\pi$,拿
\pi去跟环境做互动,当我们看到状态 s 的时候,接下来累积奖励 的期望值有多少。 -
还有一个 critic 是 $Q^{\pi}(s,a)$。
Q^{\pi}(s,a)把 s 跟 a 当作输入,它的意思是说,在状态 s 采取动作 a,接下来都用 actor\pi来跟环境进行互动,累积奖励的期望值是多少。 -
V^{\pi}输入 s,输出一个标量。 -
Q^{\pi}输入 s,然后它会给每一个 a 都分配一个 Q value。 -
你可以用 TD 或 MC 来估计。用 TD 比较稳,用 MC 比较精确。
Actor-Critic
随机变量 G 的期望值正好就是 Q ,即
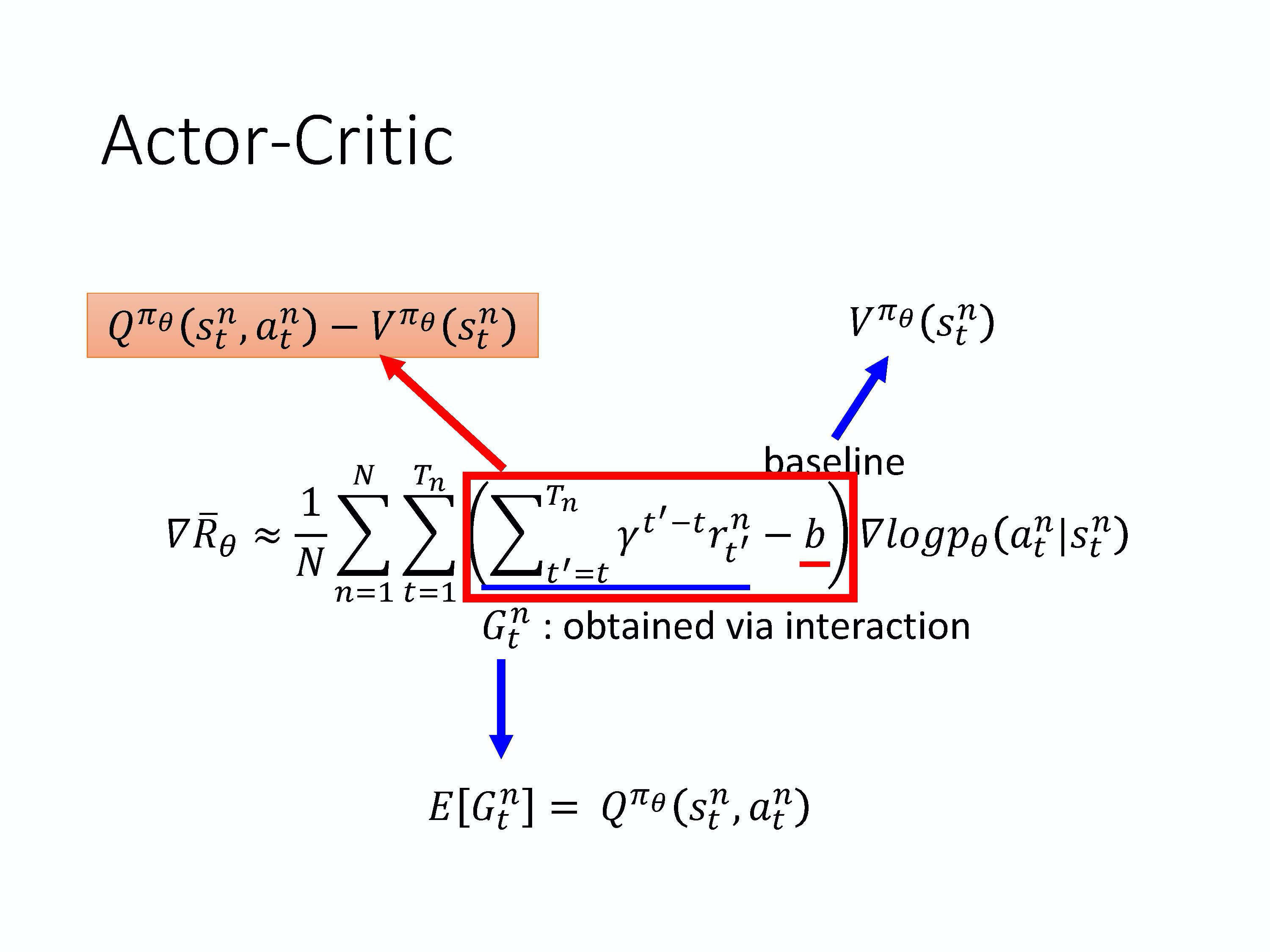
E\left[G_{t}^{n}\right]=Q^{\pi_{\theta}} \left(s_{t}^{n}, a_{t}^{n}\right)
因为这个就是 Q 的定义。Q-function 的定义就是在某一个状态 s,采取某一个动作 a,假设 policy 就是 \pi 的情况下会得到的累积奖励的期望值有多大,而这个东西就是 G 的期望值。累积奖励的期望值就是 G 的期望值。所以假设用期望值来代表 \sum_{t^{\prime}=t}^{T_{n}} \gamma^{t^{\prime}-t} r_{t^{\prime}}^{n} 这一项的话,把 Q-function 套在这里就结束了。那我们就可以 Actor 跟 Critic 这两个方法结合起来。
有不同的方法来表示 baseline,但一个常见的做法是,你用 value function V^{\pi_{\theta}}\left(s_{t}^{n}\right) 来表示 baseline。Value function 的意思是说,假设 policy 是 $\pi$,在某一个状态 s 一直互动到游戏结束,期望奖励(expected reward)有多大。 V^{\pi_{\theta}}\left(s_{t}^{n}\right) 没有涉及到动作,Q^{\pi_{\theta}}\left(s_{t}^{n}, a_{t}^{n}\right) 涉及到动作。
其实 V^{\pi_{\theta}}\left(s_{t}^{n}\right) 会是 Q^{\pi_{\theta}}\left(s_{t}^{n}, a_{t}^{n}\right) 的期望值,所以 Q^{\pi_{\theta}}\left(s_{t}^{n}, a_{t}^{n}\right)-V^{\pi_{\theta}}\left(s_{t}^{n}\right) 会有正有负,所以 \sum_{t^{\prime}=t}^{T_{n}} \gamma^{t^{\prime}-t} r_{t^{\prime}}^{n}-b 这一项就会是有正有负的。
所以我们就把 policy gradient 里面 \sum_{t^{\prime}=t}^{T_{n}} \gamma^{t^{\prime}-t} r_{t^{\prime}}^{n}-b 这一项换成了 $Q^{\pi_{\theta}}\left(s_{t}^{n}, a_{t}^{n}\right)-V^{\pi_{\theta}}\left(s_{t}^{n}\right)$。
Advantage Actor-Critic
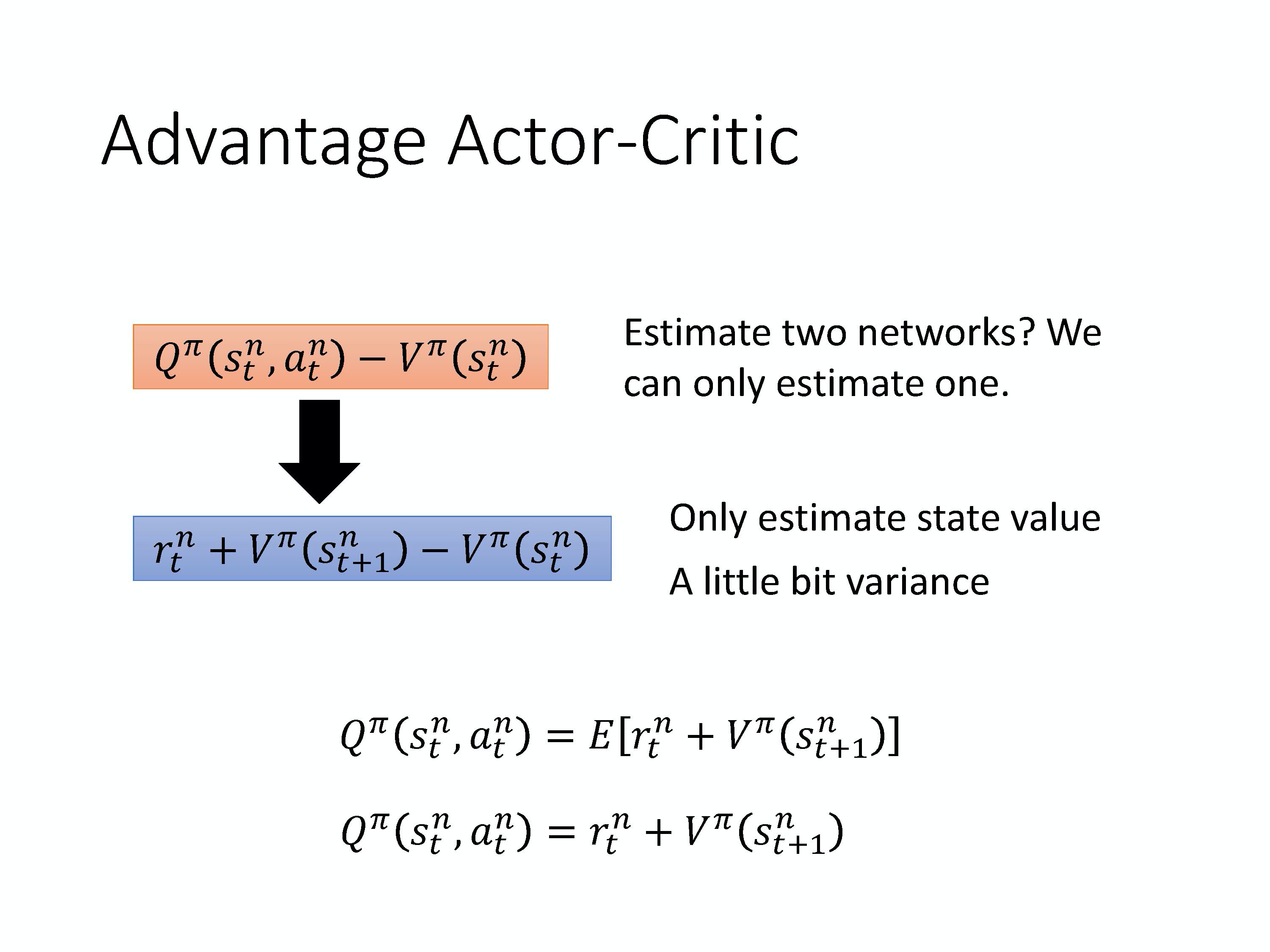
如果你这么实现的话,有一个缺点是:你要估计 2 个 网络:Q-network 和 V-network,你估测不准的风险就变成两倍。所以我们何不只估测一个网络?
事实上在这个 Actor-Critic 方法里面。你可以只估测 V 这个网络,你可以用 V 的值来表示 Q 的值,Q^{\pi}\left(s_{t}^{n}, a_{t}^{n}\right) 可以写成 r_{t}^{n}+V^{\pi}\left(s_{t+1}^{n}\right) 的期望值,即
Q^{\pi}\left(s_{t}^{n}, a_{t}^{n}\right)=E\left[r_{t}^{n}+V^{\pi}\left(s_{t+1}^{n}\right)\right]
你在状态 s 采取动作 a,会得到奖励 r,然后跳到状态 $s_{t+1}$。但是你会得到什么样的奖励 r,跳到什么样的状态 $s_{t+1}$,它本身是有随机性的。所以要把右边这个式子,取期望值它才会等于 Q-function。但我们现在把期望值这件事情去掉,即
Q^{\pi}\left(s_{t}^{n}, a_{t}^{n}\right)=r_{t}^{n}+V^{\pi}\left(s_{t+1}^{n}\right)
我们就可以把 Q-function 用 r + V 取代掉,然后得到下式:
r_{t}^{n}+V^{\pi}\left(s_{t+1}^{n}\right)-V^{\pi}\left(s_{t}^{n}\right)
把这个期望值去掉的好处就是你不需要估计 Q 了,你只需要估计 V 就够了,你只要估计 一个网络就够了。但这样你就引入了一个随机的东西 r ,它是有随机性的,它是一个随机变量。但是这个随机变量,相较于累积奖励 G 可能还好,因为它是某一个步骤会得到的奖励,而 G 是所有未来会得到的奖励的总和。G 的方差比较大,r 虽然也有一些方差,但它的方差会比 G 要小。所以把原来方差比较大的 G 换成方差比较小的 r 也是合理的。
Q: 为什么可以直接把期望值拿掉?
A: 原始的 A3C paper 试了各种方法,最后做出来就是这个最好。当然你可能说,搞不好估计 Q 和 V,也可以估计 很好,那我告诉你就是做实验的时候,最后结果就是这个最好,所以后来大家都用这个。
因为 r_{t}^{n}+V^{\pi}\left(s_{t+1}^{n}\right)-V^{\pi}\left(s_{t}^{n}\right) 叫做 Advantage function。所以这整个方法就叫 Advantage Actor-Critic。
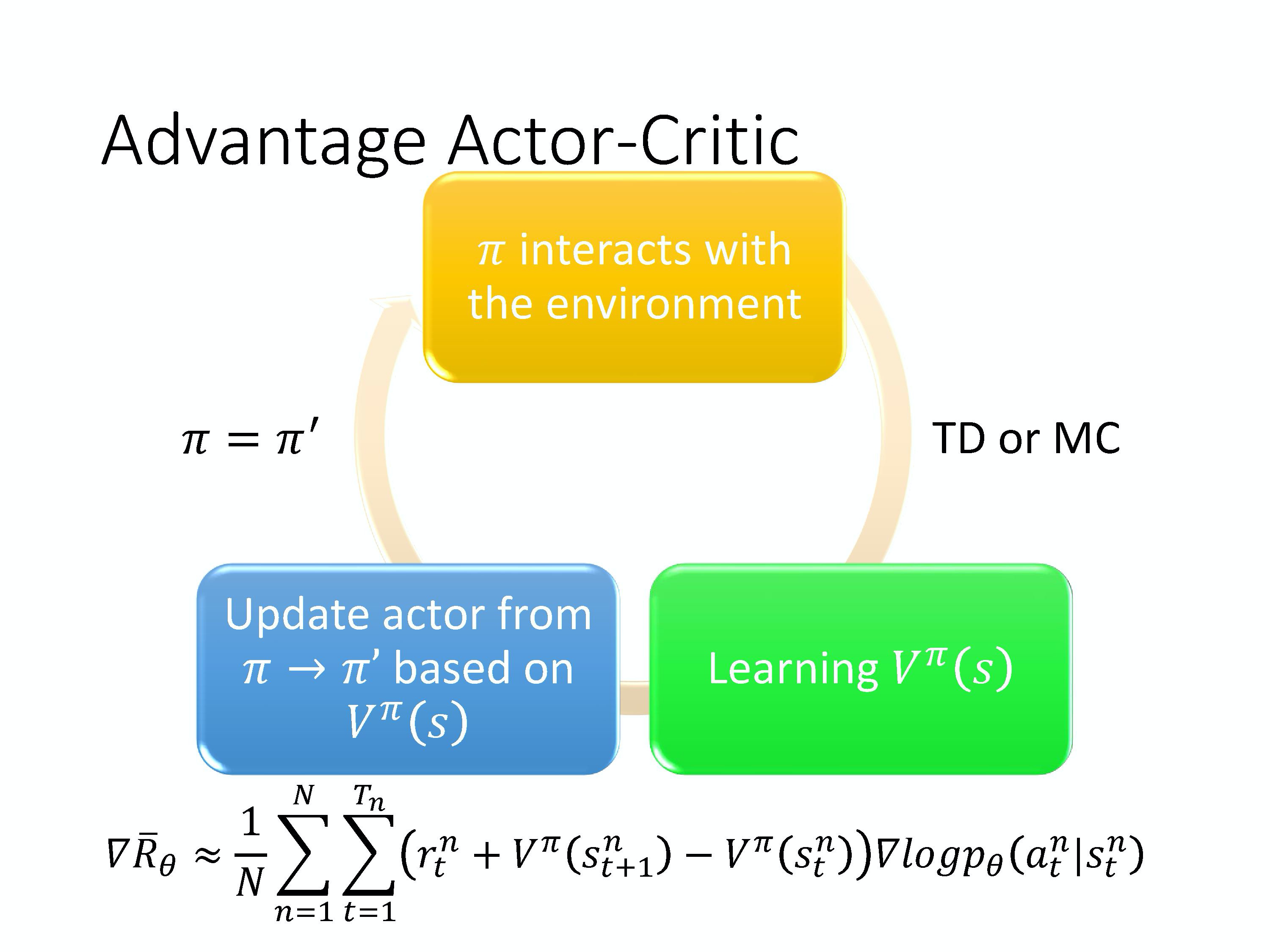
整个流程是这样子的。我们有一个 $\pi$,有个初始的 actor 去跟环境做互动,先收集资料。在 policy gradient 方法里面收集资料以后,你就要拿去更新 policy。但是在 actor-critic 方法里面,你不是直接拿那些资料去更新 policy。你先拿这些资料去估计 value function,你可以用 TD 或 MC 来估计 value function 。接下来,你再基于 value function,套用下面这个式子去更新 $\pi$。
\nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}}\left(r_{t}^{n}+V^{\pi}\left(s_{t+1}^{n}\right)-V^{\pi}\left(s_{t}^{n}\right)\right) \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right)
然后你有了新的 \pi 以后,再去跟环境互动,再收集新的资料,去估计 value function。然后再用新的 value function 去更新 policy,去更新 actor。
整个 actor-critic 的算法就是这么运作的。
实现 Actor-Critic 的时候,有两个一定会用的 tip。
- 第一个 tip 是说,我们需要估计两个网络:V function 和 policy 的网络(也就是 actor)。
- Critic 网络
V^\pi(s)输入一个状态,输出一个标量。 - Actor 网络
\pi(s)输入一个状态,- 如果动作是离散的,输出就是一个动作的分布。
- 如果动作是连续的,输出就是一个连续的向量。
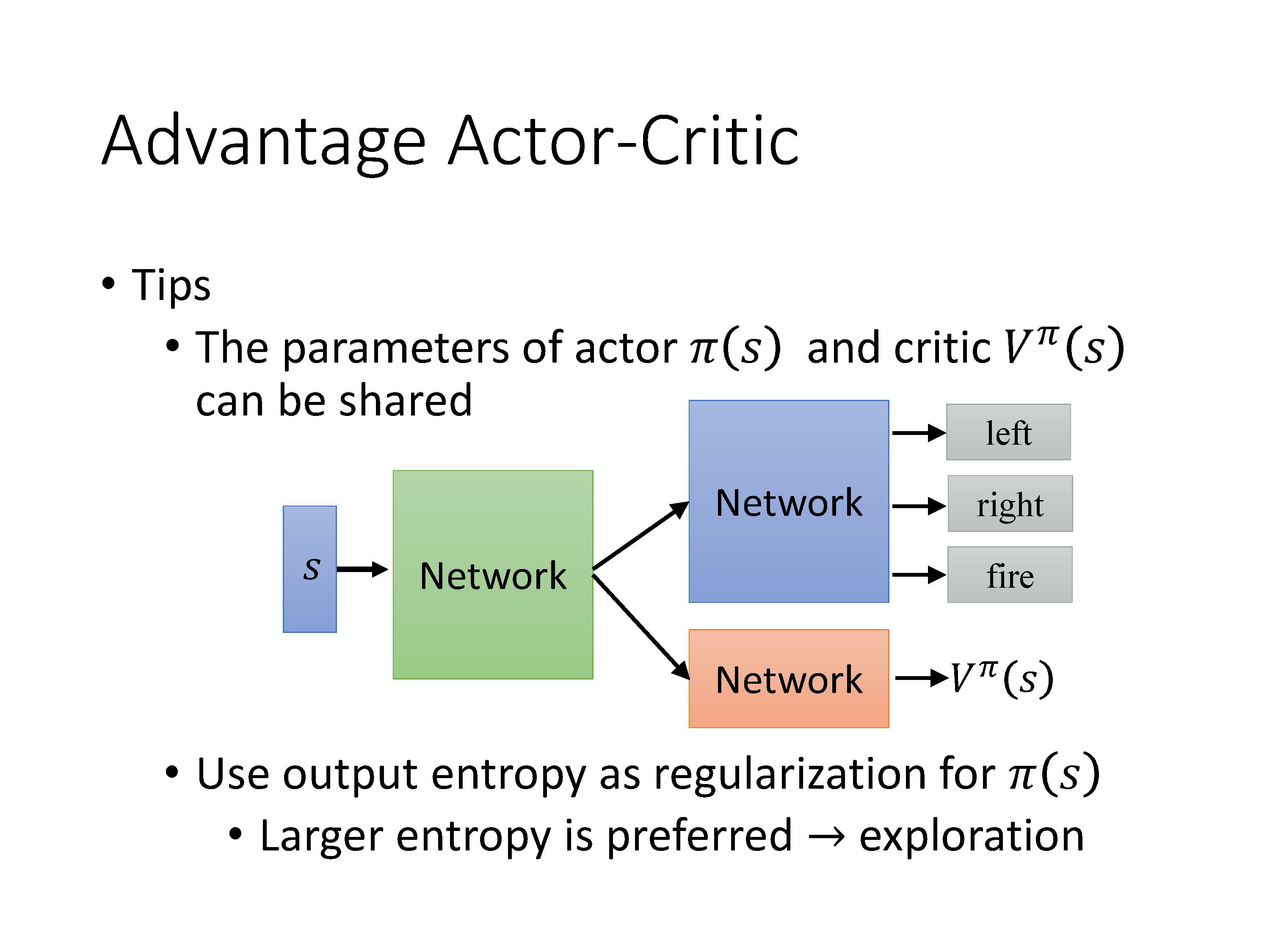
- 上图是举的是离散的例子,但连续的情况也是一样的。输入一个状态,然后它决定你现在要采取哪一个动作。这两个网络,actor 和 critic 的输入都是 s,所以它们前面几个层(layer),其实是可以共享的。
- 尤其是假设你今天是玩 Atari 游戏,输入都是图像。输入的图像都非常复杂,图像很大,通常你前面都会用一些 CNN 来处理,把那些图像抽象成高级(high level)的信息。把像素级别的信息抽象成高级信息这件事情,其实对 actor 跟 critic 来说是可以共用的。所以通常你会让 actor 跟 critic 的共享前面几个层,你会让 actor 跟 critic 的前面几个层共用同一组参数,那这一组参数可能是 CNN 的参数。
- 先把输入的像素变成比较高级的信息,然后再给 actor 去决定说它要采取什么样的行为,给这个 critic,给 value function 去计算期望奖励。
- Critic 网络
- **第二个 tip 是我们一样需要 exploration 的机制。**在做 Actor-Critic 的时候,有一个常见的 exploration 的方法是你会对你的
\pi的输出的分布下一个约束。这个约束是希望这个分布的熵(entropy)不要太小,希望这个分布的熵可以大一点,也就是希望不同的动作它的被采用的机率平均一点。这样在测试的时候,它才会多尝试各种不同的动作,才会把这个环境探索的比较好,才会得到比较好的结果。这个就是 Advantage Actor-Critic。
A3C
什么是 A3C 呢?强化学习有一个问题就是它很慢,那怎么增加训练的速度呢?这个可以讲到火影忍者就是有一次鸣人说,他想要在一周之内打败晓,所以要加快修行的速度,他老师就教他一个方法,这个方法是说你只要用影分身进行同样修行。那两个一起修行的话呢?经验值累积的速度就会变成 2 倍,所以,鸣人就开了 1000 个影分身,开始修行了。这个其实就是 Asynchronous(异步的) Advantage Actor-Critic,也就是 A3C 这个方法的精神。
A3C 这个方法就是同时开很多个 worker,那每一个 worker 其实就是一个影分身。那最后这些影分身会把所有的经验,通通集合在一起。首先你如果没有很多个 CPU,可能也是不好实现的,你可以实现 A2C 就好。
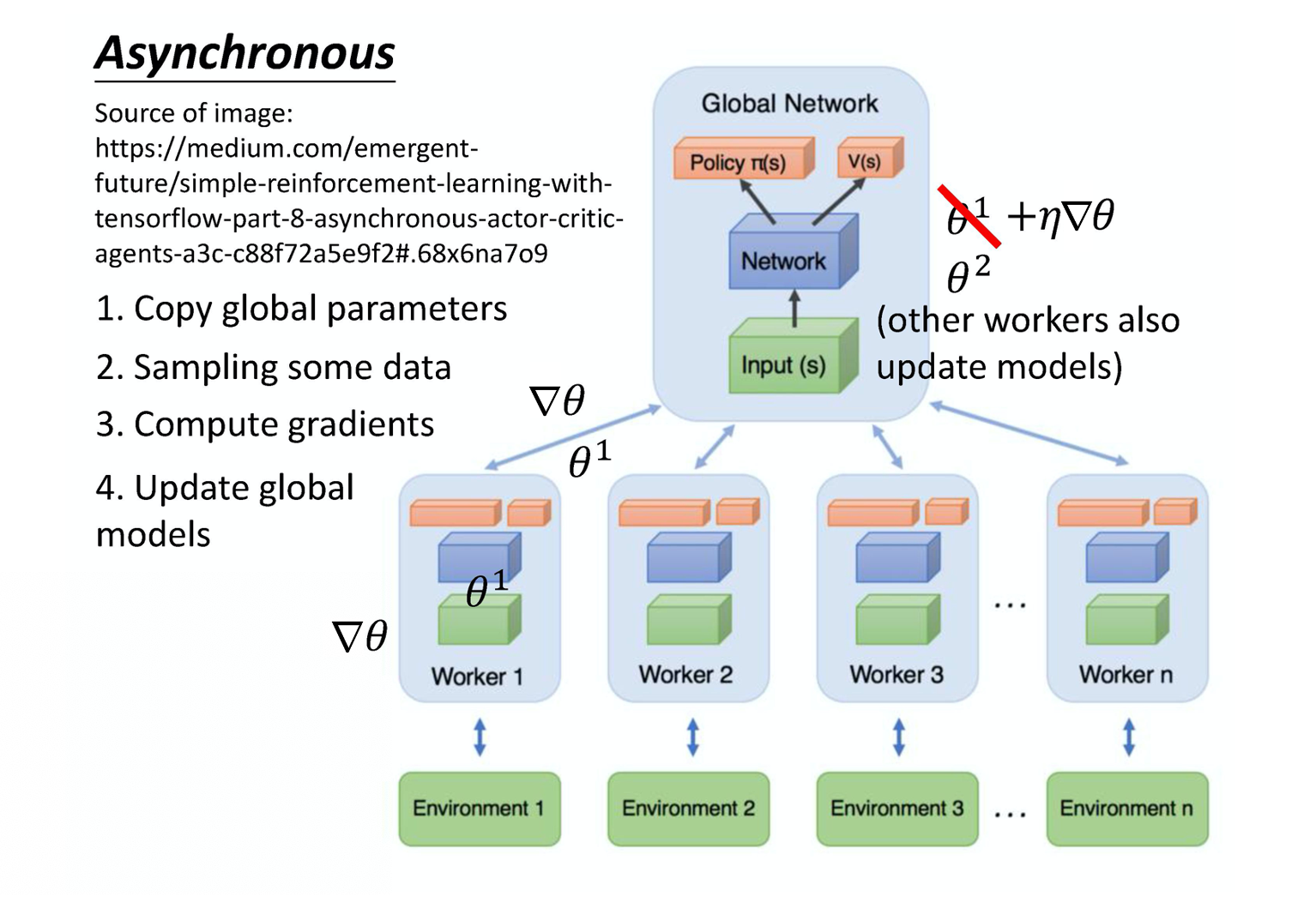
这个 A3C 是怎么运作的呢?A3C 是这样子,一开始有一个 global network。那我们刚才有讲过说,其实 policy network 跟 value network 是 tie 在一起的,它们的前几个层会被 tie 一起。我们有一个 global network,它们有包含 policy 的部分和 value 的部分。假设它的参数就是 $\theta_1$,你会开很多个 worker。每一个 worker 就用一张 CPU 去跑,比如你就开 8 个 worker ,那你至少 8 张 CPU。第一个 worker 就把 global network 的参数复制过来,每一个 worker 工作前都会 global network 的参数复制过来。接下来你就去跟环境做互动,每一个 actor 去跟环境做互动的时候,为了要收集到比较 diverse 的数据,所以举例来说如果是走迷宫的话,可能每一个 actor 起始的位置都会不一样,这样它们才能够收集到比较多样性的数据。每一个 actor 就自己跟环境做互动,互动完之后,你就会计算出梯度。那计算出梯度 以后,你要拿梯度去更新你的参数。你就计算一下你的梯度,然后用你的梯度去更新 global network 的参数。就是这个 worker 算出梯度以后,就把梯度传回给中央的控制中心。然后中央的控制中心,就会拿这个梯度去更新原来的参数。但是要注意一下,所有的 actor 都是平行跑的,就每一个 actor 就是各做各的,互相之间就不要管彼此。所以每个人都是去要了一个参数以后,做完就把参数传回去。所以当第一个 worker 做完想要把参数传回去的时候,本来它要的参数是 $\theta_1$,等它要把梯度传回去的时候。可能别人已经把原来的参数覆盖掉,变成 $\theta_2$了。但是没有关系,它一样会把这个梯度就覆盖过去就是了。Asynchronous actor-critic 就是这么做的,这个就是 A3C。
Pathwise Derivative Policy Gradient
讲完 A3C 之后,我们要讲另外一个方法叫做 Pathwise Derivative Policy Gradient。这个方法很神奇,它可以看成是 Q-learning 解连续动作的一种特别的方法,也可以看成是一种特别的 Actor-Critic 的方法。
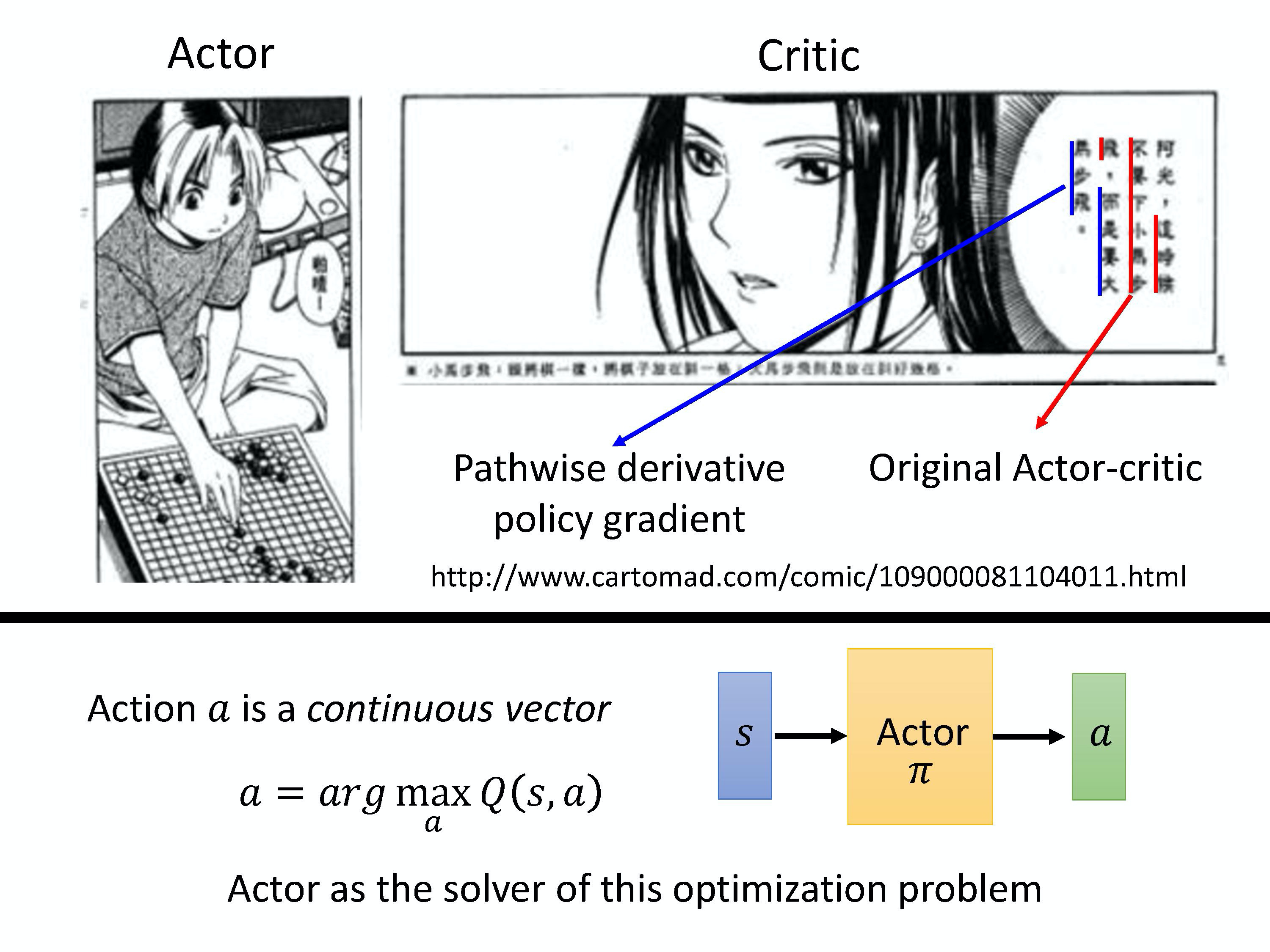
用棋灵王来比喻的话,阿光是一个 actor,佐为是一个 critic。阿光落某一子以后呢,如果佐为是一般的 Actor-Critic,他会告诉他说这时候不应该下小马步飞,他会告诉你,你现在采取的这一步算出来的 value 到底是好还是不好,但这样就结束了,他只告诉你说好还是不好。因为一般的这个 Actor-Critic 里面那个 critic 就是输入状态或输入状态跟动作的 pair,然后给你一个 value 就结束了。所以对 actor 来说,它只知道它做的这个行为到底是好还是不好。但如果是在 pathwise derivative policy gradient 里面,这个 critic 会直接告诉 actor 说采取什么样的动作才是好的。所以今天佐为不只是告诉阿光说,这个时候不要下小马步飞,同时还告诉阿光说这个时候应该要下大马步飞,所以这个就是 Pathwise Derivative Policy Gradient 中的 critic。critic 会直接告诉 actor 做什么样的动作才可以得到比较大的 value。
从 Q-learning 的观点来看,Q-learning 的一个问题是你没有办法在用 Q-learning 的时候,考虑 continuous vector。其实也不是完全没办法,就是比较麻烦,比较没有通用的解决方法(general solution),我们怎么解这个优化问题呢?我们用一个 actor 来解这个优化的问题。本来在 Q-learning 里面,如果是一个连续的动作(continuous action),我们要解这个优化问题。但是现在这个优化问题由 actor 来解,我们假设 actor 就是一个 solver,这个 solver 的工作就是给你状态, s,然后它就去解解告诉我们说,哪一个动作可以给我们最大的 Q value,这是从另外一个观点来看 pathwise derivative policy gradient 这件事情。这个说法,你有没有觉得非常的熟悉呢?我们在讲 GAN 的时候,不是也讲过一个说法。我们学习一个 discriminator,它是要评估东西好不好,discriminator 要自己生成东西,非常的困难,那怎么办?因为要解一个 arg max 的问题非常的困难,所以用 generator 来生成。所以今天的概念其实是一样的,Q 就是那个 discriminator。要根据这个 discriminator 决定动作非常困难,怎么办?另外学习一个网络来解这个优化问题,这个东西就是 actor。所以,两个不同的观点是同一件事,从两个不同的观点来看,一个观点是说,我们可以对原来的 Q-learning 加以改进,怎么改进呢?我们学习一个 actor 来决定动作以解决 arg max 不好解的问题。或是另外一个观点是,原来的 actor-critic 的问题是 critic 并没有给 actor 足够的信息,它只告诉它好或不好,没有告诉它说什么样叫好,那现在有新的方法可以直接告诉 actor 说,什么样叫做好。
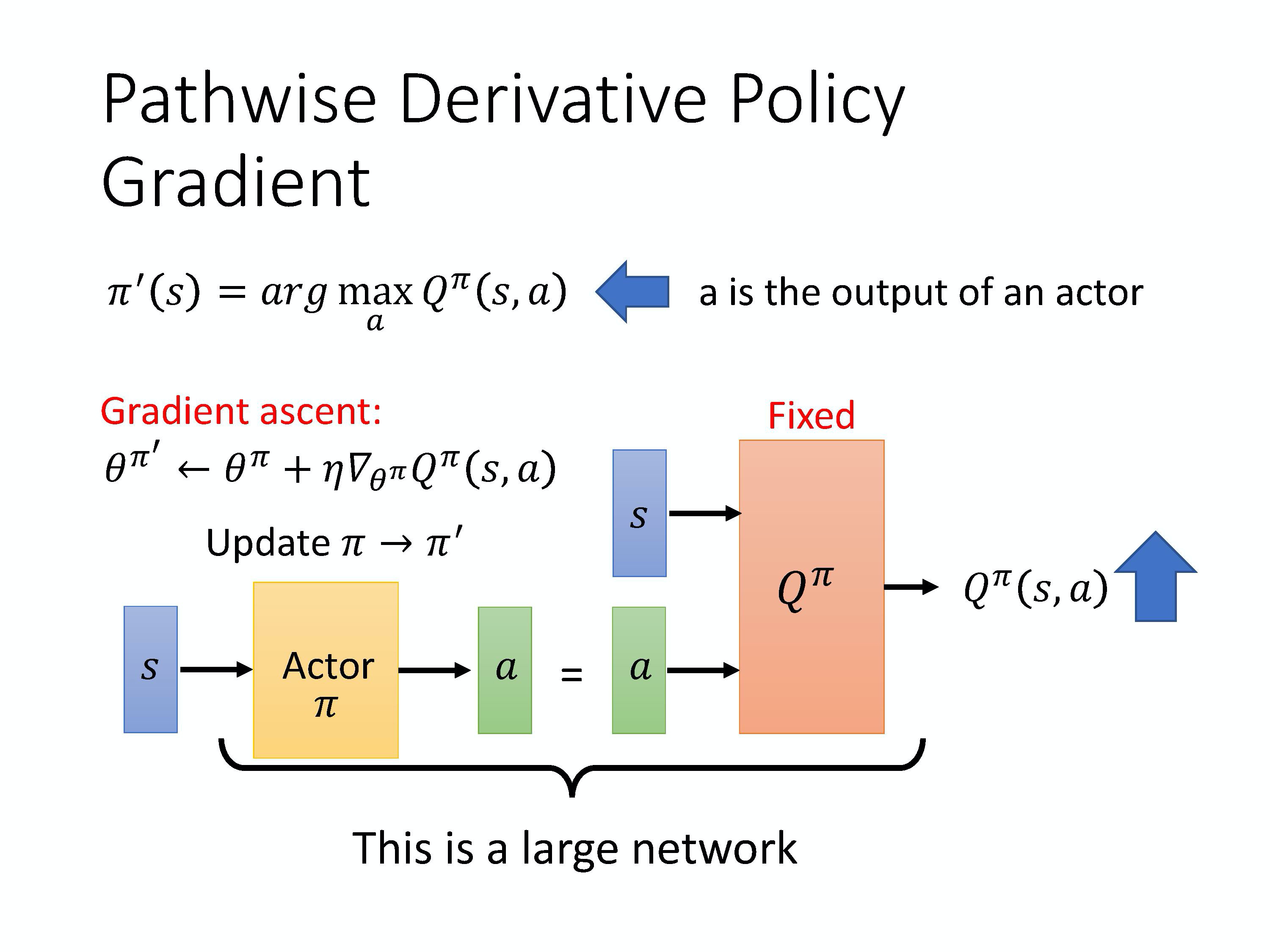
那我们讲一下它的算法。假设我们学习了一个 Q-function,Q-function 就是输入 s 跟 a,输出就是 $Q^{\pi}(s,a)$。那接下来,我们要学习一个 actor,这个 actor 的工作就是解这个 arg max 的问题。这个 actor 的工作就是输入一个状态 s,希望可以输出一个动作 a。这个动作 a 被丢到 Q-function 以后,它可以让 Q^{\pi}(s,a) 的值越大越好。
那实际上在训练的时候,你其实就是把 Q 跟 actor 接起来变成一个比较大的网络。Q 是一个网络,输入 s 跟 a,输出一个 value。Actor 在训练的时候,它要做的事情就是输入 s,输出 a。把 a 丢到 Q 里面,希望输出的值越大越好。在训练的时候会把 Q 跟 actor 接起来,当作是一个大的网络。然后你会固定住 Q 的参数,只去调 actor 的参数,就用 gradient ascent 的方法去最大化 Q 的输出。这就是一个 GAN,这就是 conditional GAN。Q 就是 discriminator,但在强化学习就是 critic,actor 在 GAN 里面就是 generator,其实它们就是同一件事情。
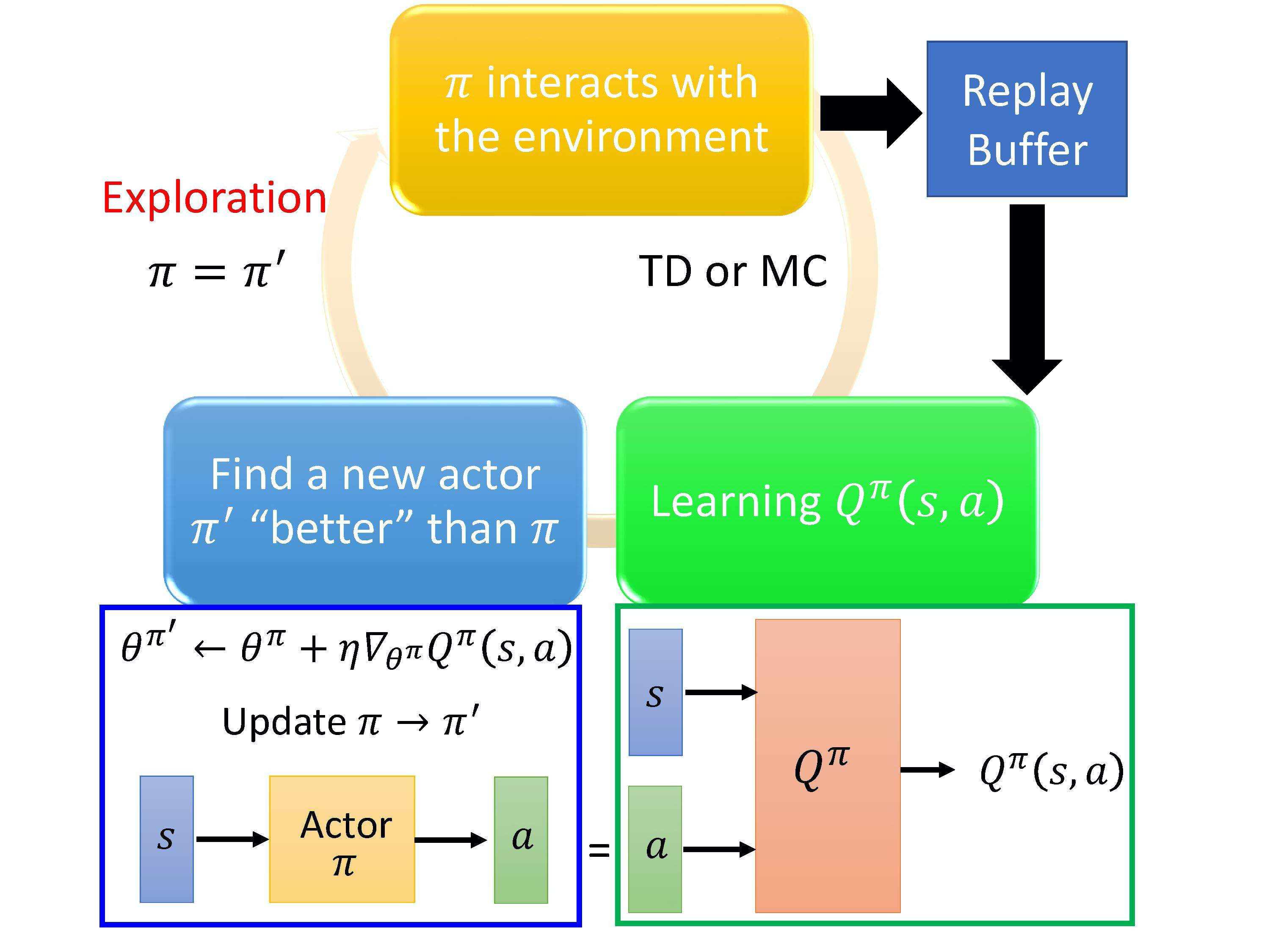
我们来看一下 pathwise derivative policy gradient 的算法。一开始你会有一个 actor $\pi$,它去跟环境互动,然后,你可能会要它去估计 Q value。估计完 Q value 以后,你就把 Q value 固定,只去学习一个 actor。假设这个 Q 估得是很准的,它知道在某一个状态采取什么样的动作,会真的得到很大的 value。接下来就学习这个 actor,actor 在给定 s 的时候,它采取了 a,可以让最后 Q-function 算出来的 value 越大越好。你用这个 criteria 去更新你的 actor $\pi$。然后有新的 \pi 再去跟环境做互动,再估计 Q,再得到新的 \pi 去最大化 Q 的输出。本来在 Q-learning 里面,你用得上的技巧,在这边也几乎都用得上,比如说 replay buffer、exploration 等等。
上图是原来 Q-learning 的算法。你有一个 Q-function Q,你有另外一个目标的 Q-function 叫做 $\hat{Q}$。然后在每一次 训练,在每一个回合的每一个时间点里面,你会看到一个状态 $s_t$,你会采取某一个动作 $a_{t}$。至于采取哪一个动作是由 Q-function 所决定的,因为解一个 arg max 的问题。如果是离散的话没有问题,你就看说哪一个 a 可以让 Q 的 value 最大,就采取哪一个动作。那你需要加一些 exploration,这样 performance 才会好。你会得到奖励 $r_t$,跳到新的状态 $s_{t+1}$。你会把 s_t, a_{t}, r_t, s_{t+1} 塞到你的 buffer 里面去。你会从你的 buffer 里面采样一个 batch 的 data,这个 batch data 里面,可能某一笔是 $s_i, a_i, r_i, s_{i+1}$。接下来你会算一个目标,这个目标叫做 y ,$y=r_{i}+\max {a} \hat{Q}\left(s{i+1}, a\right)$。然后怎么学习你的 Q 呢?你希望 Q(s_i,a_i) 跟 y 越接近越好,这是一个回归的问题,最后每 C 个步骤,你要把用 Q 替代 \hat{Q} 。
接下来我们把 Q-learning 改成 Pathwise Derivative Policy Gradient,这边需要做四个改变。
- 第一个改变是,你要把 Q 换成 $\pi$,本来是用 Q 来决定在状态
s_t产生那一个动作,a_{t}现在是直接用\pi。我们不用再解 arg max 的问题了,我们直接学习了一个 actor。这个 actor 输入s_t就会告诉我们应该采取哪一个 $a_{t}$。所以本来输入 $s_t$,采取哪一个 $a_t$,是 Q 决定的。在 Pathwise Derivative Policy Gradient 里面,我们会直接用\pi来决定,这是第一个改变。 - 第二个改变是,本来这个地方是要计算在 $s_{i+1}$,根据你的 policy 采取某一个动作 a 会得到多少的 Q value。那你会采取让
\hat{Q}最大的那个动作 a。那现在因为我们其实不好解这个 arg max 的问题,所以 arg max 问题,其实现在就是由 policy\pi来解了,所以我们就直接把s_{i+1}代到 policy\pi里面,你就会知道说 givens_{i+1},哪一个动作会给我们最大的 Q value,那你在这边就会采取那一个动作。在 Q-function 里面,有两个 Q network,一个是真正的 Q network,另外一个是目标 Q network。那实际上你在实现这个算法 的时候,你也会有两个 actor,你会有一个真正要学习的 actor $\pi$,你会有一个目标 actor\hat{\pi}。这个原理就跟为什么要有目标 Q network 一样,我们在算目标 value 的时候,我们并不希望它一直的变动,所以我们会有一个目标的 actor 和一个目标的 Q-function,它们平常的参数就是固定住的,这样可以让你的这个目标的 value 不会一直地变化。所以本来到底是要用哪一个动作 a,你会看说哪一个动作 a 可以让\hat{Q}最大。但现在因为哪一个动作 a 可以让\hat{Q}最大这件事情已经被用那个 policy 取代掉了,所以我们要知道哪一个动作 a 可以让\hat{Q}最大,就直接把那个状态带到\hat{\pi}里面,看它得到哪一个 a,就用那一个 a,那一个 a 就是会让\hat{Q}(s,a)的值最大的那个 a 。其实跟原来的这个 Q-learning 也是没什么不同,只是原来你要解 arg max 的地方,通通都用 policy 取代掉了,那这个是第二个不同。 - 第三个不同就是之前只要学习 Q,现在你多学习一个 $\pi$,那学习
\pi的时候的方向是什么呢?学习\pi的目的,就是为了最大化 Q-function,希望你得到的这个 actor,它可以让你的 Q-function 输出越大越好,这个跟学习 GAN 里面的 generator 的概念。其实是一样的。 - 第四个步骤,就跟原来的 Q-function 一样。你要把目标的 Q network 取代掉,你现在也要把目标 policy 取代掉。
Connection with GAN
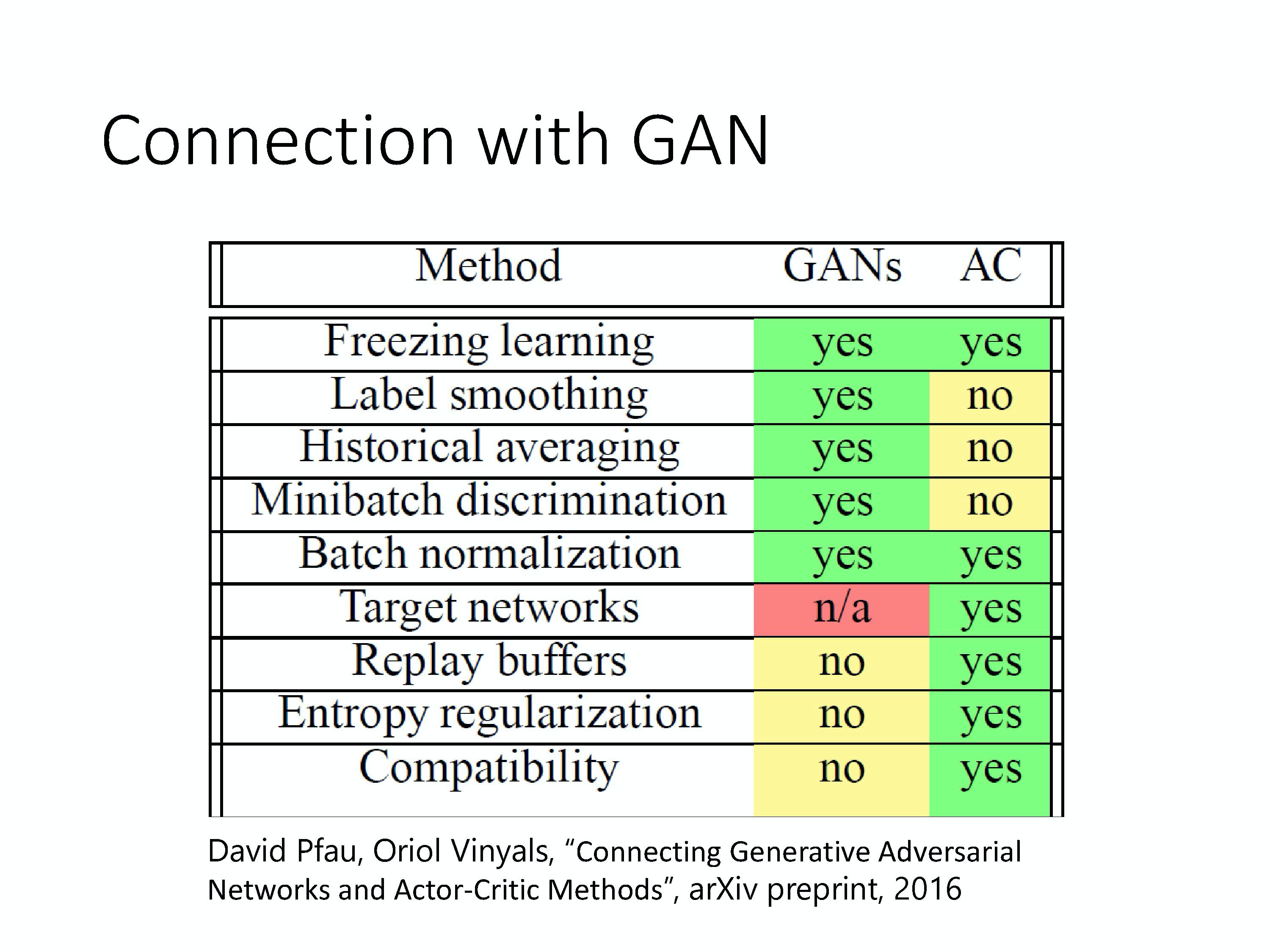
其实 GAN 跟 Actor-Critic 的方法是非常类似的。这边就不细讲,你可以去找到一篇 paper 叫做 Connecting Generative Adversarial Network and Actor-Critic Methods。
Q: 知道 GAN 跟 Actor-Critic 非常像有什么帮助呢?
A: 一个很大的帮助就是 GAN 跟 Actor-Critic 都是以难训练而闻名的。所以在文献上就会收集各式各样的方法,告诉你说怎么样可以把 GAN 训练起来。怎么样可以把 Actor-Critic 训练起来。但是因为做 GAN 跟 Actor-Critic 的人是两群人,所以这篇 paper 里面就列出说在 GAN 上面有哪些技术是有人做过的,在 Actor-Critic 上面,有哪些技术是有人做过的。也许在 GAN 上面有试过的技术,你可以试着应用在 Actor-Critic 上,在 Actor-Critic 上面做过的技术,你可以试着应用在 GAN 上面,看看是否 work。