纸质版勘误修订表

如何使用勘误？首先找到你的书的印次，接下来对着下表索引印次，该印次之后所有的勘误都是你的书中所要注意的勘误，印次前的所有勘误在当印次和之后印次均已印刷修正。为方便读者，所有修订内容都列举在此。其中部分修订是为了更便于读者理解，并非原文有误。

第1版第3次印刷（2022.07）

前勒口作者简介：
- 王琦：中国科学院大学硕士在读 → 中国科学院大学硕士
- 杨毅远：清华大学硕士在读 → 清华大学硕士
- 江季：北京大学硕士在读 → 北京大学硕士
38页，式(2.7)下面一段第1行：s^{\prime} 可以看成未来的所有状态 → s^{\prime} 可以看成未来的某个状态
38页，式(2.7)下面一段第2行：未来某一个状态的价值 → 未来某个状态的价值
52页，第二段修改为：

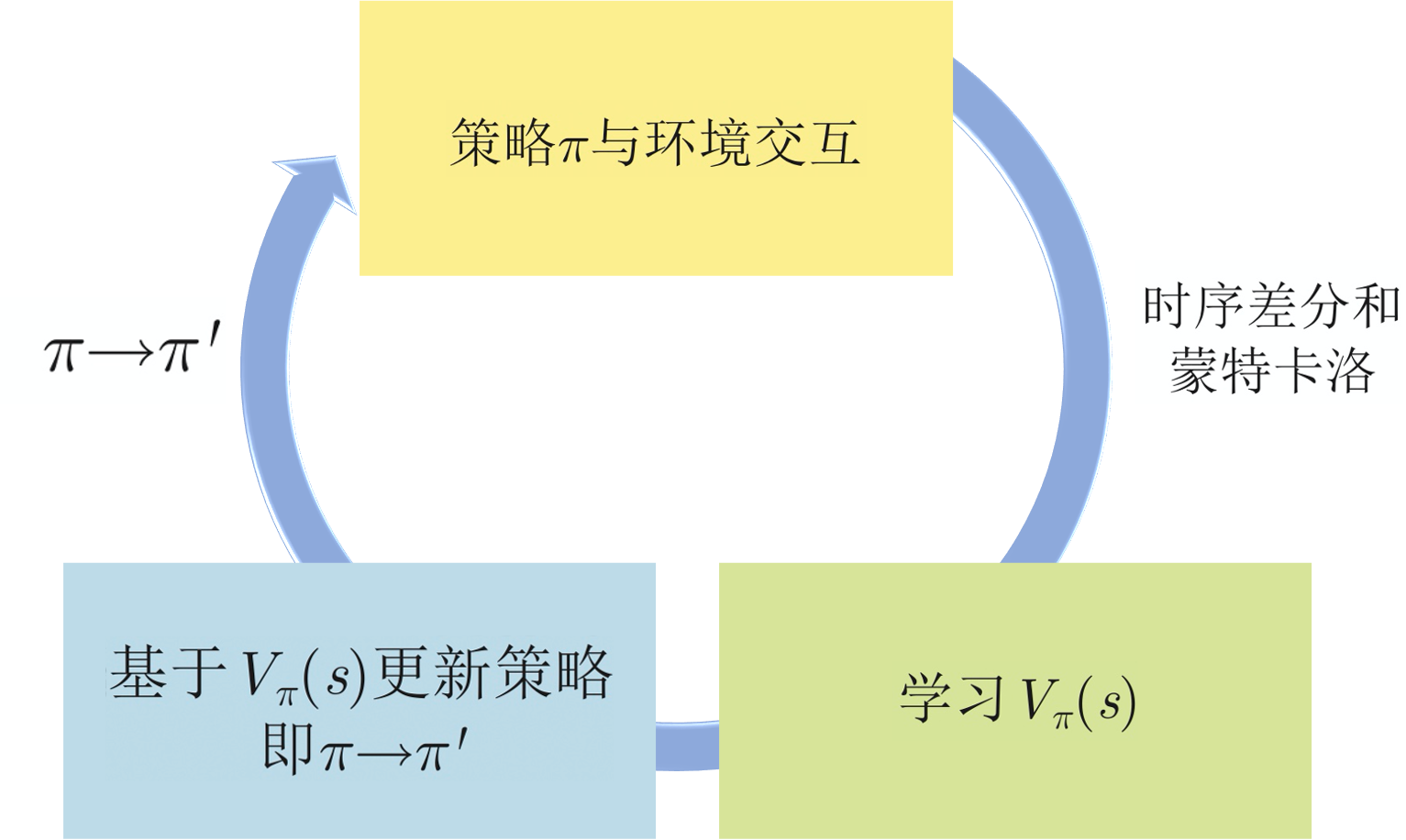
举一个例子来说明预测与控制的区别。首先是预测问题。在图 2.16（a）的方格中，智能体可以采取上、下、左、右4个动作。如果采取的动作让智能体走出网格，则其会在原位置不动，并且得到 -1 的奖励。除了将智能体从 \mathrm{A} 和 \mathrm{B} 移走的动作外，其他动作的奖励均为 0。智能体在 \mathrm{A} 采取任意一个动作，都会移动到 \mathrm{A}^{\prime} ，并且得到 +10 的奖励。智能体在 \mathrm{B} 采取任意一个动作，都会移动到 \mathrm{B}^{\prime} ，并且得到 +5 的奖励。如图 2.16（b）所示，现在，我们给定一个策略：在任何状态中，智能体的动作模式都是随机的，也就是上、下、左、右的概率均为 0.25。预测问题要做的就是，求出在这种决策模式下的价值函数。图 2.16 （c）是折扣因子为 \gamma=0.9 时对应的价值函数。

55页，第2段的第1行：p(2 \mid 6, \mathrm{u})=2 → p(2 \mid 6, \mathrm{u})=1
134页，式(5.16)下面一段第2行：最大化式 (5.16) → 最大化式 (5.15)
189页，图9.4替换成下图：

第1版第2次印刷（2022.06）

1页，图1.1删除参考文献：SUTTON R S, BARTO A G. Reinforcement learning: An introduction (second edition)[M]. London: The MIT Press, 2018
7页的图1.9和8页的图1.10加参考文献：Sergey Levine的课程“Deep Reinforcement Learning”
19页，图1.19删除参考文献：David Silver 的课程“UCL Course on RL”
24页，第一段下面的代码下面加入注解：

上面这段代码只是示例，其目的是让读者了解强化学习算法代码实现的框架，并非完整代码，load_agent 函数并未定义，所以运行这段代码会报错。

33页，图2.1删除参考文献：SUTTON R S, BARTO A G. Reinforcement learning: An introduction(second edition)[M]. London:The MIT Press, 2018
36页，式(2.4)上面一段第2行和第3行：**回报（return）**是指把奖励进行折扣后所获得的奖励。回报可以定义为奖励的逐步叠加，即 → **回报（return）**可以定义为奖励的逐步叠加，假设时刻$t$后的奖励序列为$r_{t+1},r_{t+2},r_{t+3},\cdots$，则回报为
36页，式(2.4)下面一段第1行：这里有一个折扣因子，→ 其中，$T$是最终时刻，\gamma 是折扣因子，
100页，第2段的第2行：0、1、2、3 这 4 个数对应上、下、左、右 → 0、1、2、3 这 4 个数对应上、右、下、左
108页，图4.4替换成下图：

151页，第2段的倒数第1行：均方误差（mean square error）→ 均方误差（mean square error，MSE）
201页，第3段的倒数第2行：均方误差（mean squared error，MSE）→ 均方误差
223页，第1段的第4行删除参考文献：周志华. 机器学习 [M]. 北京：清华大学出版社, 2016
241页，第1段的第3行和第4行：均方误差（mean square error，MSE）→ 均方误差

第1版第1次印刷（2022.03）

2页，2.1.2节的标题：马尔可夫过程/马尔可夫链 → 马尔可夫链
17页，第一段的倒数第4行：策略梯度 → 策略梯度（policy gradient，PG）
34页，2.1.2节的标题：马尔可夫过程/马尔可夫链 → 马尔可夫链
34页，2.1.2节的第2段的第1行：也称为马尔可夫链（Markov chain）。 → 也称为马尔可夫链（Markov chain）。马尔可夫链是最简单的马尔可夫过程，其状态是有限的。
35页的图2.2 和 41页的图2.5（a）替换成下图：

47页，2.3.5节的第3行：称为备份图（backup diagram） → 称为备份图（backup diagram）或回溯图
61页，2.3.12节的第1小节的第2段的第1行：\pi(s|a) → \pi(a|s)
62页，式(2.55) 前第2行：H 是迭代次数 → H 是让 V(s) 收敛所需的迭代次数
62页，式(2.57) 改为


\pi(s)=\underset{a}{\arg \max } \left[R(s, a)+\gamma \sum_{s^{\prime} \in S} p\left(s^{\prime} \mid s, a\right) V_{H+1}\left(s^{\prime}\right)\right]

70页，第一段修改为：

策略最简单的表示是查找表（look-up table），即表格型策略（tabular policy）。使用查找表的强化学习方法称为表格型方法（tabular method），如蒙特卡洛、Q学习和Sarsa。本章通过最简单的表格型方法来讲解如何使用基于价值的方法求解强化学习问题。

76页，式(3.1) 中 G 和 r 后面的数字改为下标，即


\begin{array}{l}
G_{13}=0 \\
G_{12}=r_{13}+\gamma G_{13}=-1+0.6 \times 0=-1 \\
G_{11}=r_{12}+\gamma G_{12}=-1+0.6 \times(-1)=-1.6 \\
G_{10}=r_{11}+\gamma G_{11}=-1+0.6 \times(-1.6)=-1.96 \\
G_9=r_{10}+\gamma G_{10}=-1+0.6 \times(-1.96)=-2.176 \approx-2.18 \\
G_8=r_9+\gamma G_9=-1+0.6 \times(-2.176)=-2.3056 \approx-2.3
\end{array}

89页，图3.25的倒数第4行：如果$(s_t,a_t)$没有出现 → 如果(s_t,a_t) 出现
101页中间一段下面的代码和102页最上面的代码的缩进有问题，改为

rewards = []
ma_rewards = [] # 滑动平均奖励
for i_ep in range(cfg.train_eps):
    ep_reward = 0 # 记录每个回合的奖励
    state = env.reset() # 重置环境, 重新开始（开始一个新的回合）
    while True:
        action = agent.choose_action(state) # 根据算法选择一个动作
        next_state, reward, done, _ = env.step(action) # 与环境进行一次动作交互
        agent.update(state, action, reward, next_state, done) # Q学习算法更新
        state = next_state # 存储上一个观察值
        ep_reward += reward
        if done:
            break
    rewards.append(ep_reward)
    if ma_rewards:
        ma_rewards.append(ma_rewards[-1]*0.9+ep_reward*0.1)
    else:
        ma_rewards.append(ep_reward)

103页，图3.37上面一段：具体可以查看 GitHub 上的源码 → 具体可以查看本书配套代码
106页，4.1节上面添加以下文字：

策略梯度算法是基于策略的方法，其对策略进行了参数化。假设参数为 \theta 的策略为 $\pi_{\theta}$，该策略为随机性策略，其输入某个状态，输出一个动作的概率分布。策略梯度算法不需要在动作空间中最大化价值，因此较为适合解决具有高维或者连续动作空间的问题。

140页，6.1节上面一段的第1行：深度 Q 网络（Deep Q-network，DQN）→ 深度 Q 网络（deep Q-network，DQN）
140页，6.1节上面添加以下文字：

深度 Q 网络算法的核心是维护 Q 函数并使用其进行决策。Q_{\pi}(s,a) 为在该策略 \pi 下的动作价值函数，每次到达一个状态 s_t 之后，遍历整个动作空间，使用让 Q_{\pi}(s,a) 最大的动作作为策略：


a_{t}=\underset{a}{\arg \max } ~Q_{\pi}\left(s_{t}, a\right) \tag{6.2}

深度 Q 网络采用贝尔曼方程来迭代更新 Q_{\pi}(s,a) ：


Q_{\pi}\left(s_{t}, a_{t}\right) \leftarrow Q_{\pi}\left(s_{t}, a_{t}\right)+\alpha\left(r_{t}+\gamma \max _{a} Q_{\pi}\left(s_{t+1}, a\right)-Q_{\pi}\left(s_{t}, a_{t}\right)\right) \tag{6.3}

通常在简单任务上，使用全连接神经网络（fully connected neural network）来拟合 $Q_{\pi}$，但是在较为复杂的任务上（如玩雅达利游戏），会使用卷积神经网络来拟合从图像到价值函数的映射。由于深度 Q 网络的这种表达形式只能处理有限个动作值，因此其通常用于处理离散动作空间的任务。

140页后的公式编号需要进行更新。
145页，式(6.6) 下面一段的第1行：所以状态 s_b 的奖励等于 → 所以状态 s_a 的奖励等于
149页，式(6.15) 改为


\begin{aligned}
V^{\pi}(s) &\le Q^{\pi}(s,\pi'(s)) \\
&=E\left[r_{t}+V^{\pi}\left(s_{t+1}\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right]\\
&\le E\left[r_{t}+Q^{\pi}\left(s_{t+1}, \pi^{\prime}\left(s_{t+1}\right)\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\
&=E\left[r_{t}+r_{t+1}+V^{\pi}\left(s_{t+2}\right) |s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right]  \\
& \le E\left[r_{t}+r_{t+1}+Q^{\pi}\left(s_{t+2},\pi'(s_{t+2}\right) | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\
& = E\left[r_{t}+r_{t+1}+r_{t+2}+V^{\pi}\left(s_{t+3}\right) |s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right] \\
& \le \cdots\\
& \le E\left[r_{t}+r_{t+1}+r_{t+2}+\cdots | s_{t}=s, a_{t}=\pi^{\prime}\left(s_{t}\right)\right]  \\
& = V^{\pi'}(s)
\end{aligned}

154页，6.5节第1段的第5行：每一笔数据就是记得说，我们之前 → 每一笔数据是一个四元组（状态、动作、奖励、下一状态），即我们之前
156页，6.6节第1段的第2行：一开始目标 Q 网络 → 一开始目标网络 \hat{Q}
156页，式(6.22) 下面一段的第1行：在状态 s_{i+1} 会采取的动作 a 就是可以让 Q → 在状态 s_{i+1} 会采取的动作 a 就是可以让 \hat{Q}
176页，第1行：全连接网络 → 全连接神经网络
176页，第1行下面的代码块：初始化 Q 网络，为全连接网络 → 初始化 Q 网络为全连接神经网络
187页，图9.2的标题：深度 Q 网络 → 深度 Q 网络的两种评论员
187页，9.3节的标题：演员-评论员算法 → 优势演员-评论员算法
187页，倒数第1行：$Q_{\pi_{\theta}}\left(s_{t}^{n}, a_{t}^{n}\right)-V_{\pi_{\theta}}\left(s_{t}^{n}\right)$。→ 优势函数$A^{\theta}\left(s^{n}{t}, a^{n}{t}\right)$，即 $Q_{\pi_{\theta}}\left(s_{t}^{n}, a_{t}^{n}\right)-V_{\pi_{\theta}}\left(s_{t}^{n}\right)$。因此该算法称为优势演员-评论员算法。
188页，图9.3的标题：演员-评论员算法 → 优势演员-评论员算法
188页，删除9.4节的标题，目录对应的部分也需要修改
188页，9.4节的第一段的第1行：原始的演员-评论员算法 → 原始的优势演员-评论员算法
188页，式(9.5)的上面一行：可得 → 可得时序差分误差
189页，删除第4行到第5行的文字：因为 r_{t}^{n}+V_{\pi}\left(s_{t+1}^{n}\right)-V_{\pi}\left(s_{t}^{n}\right) 被称为优势函数，所以该算法被称为优势演员-评论员算法。
190页，9.5节第2段的第3行：也是不好实现的。我们可以实现优势演员-评论员算法就可以。 → 不好实现异步优势演员-评论员算法，但可以实现优势演员-评论员算法。
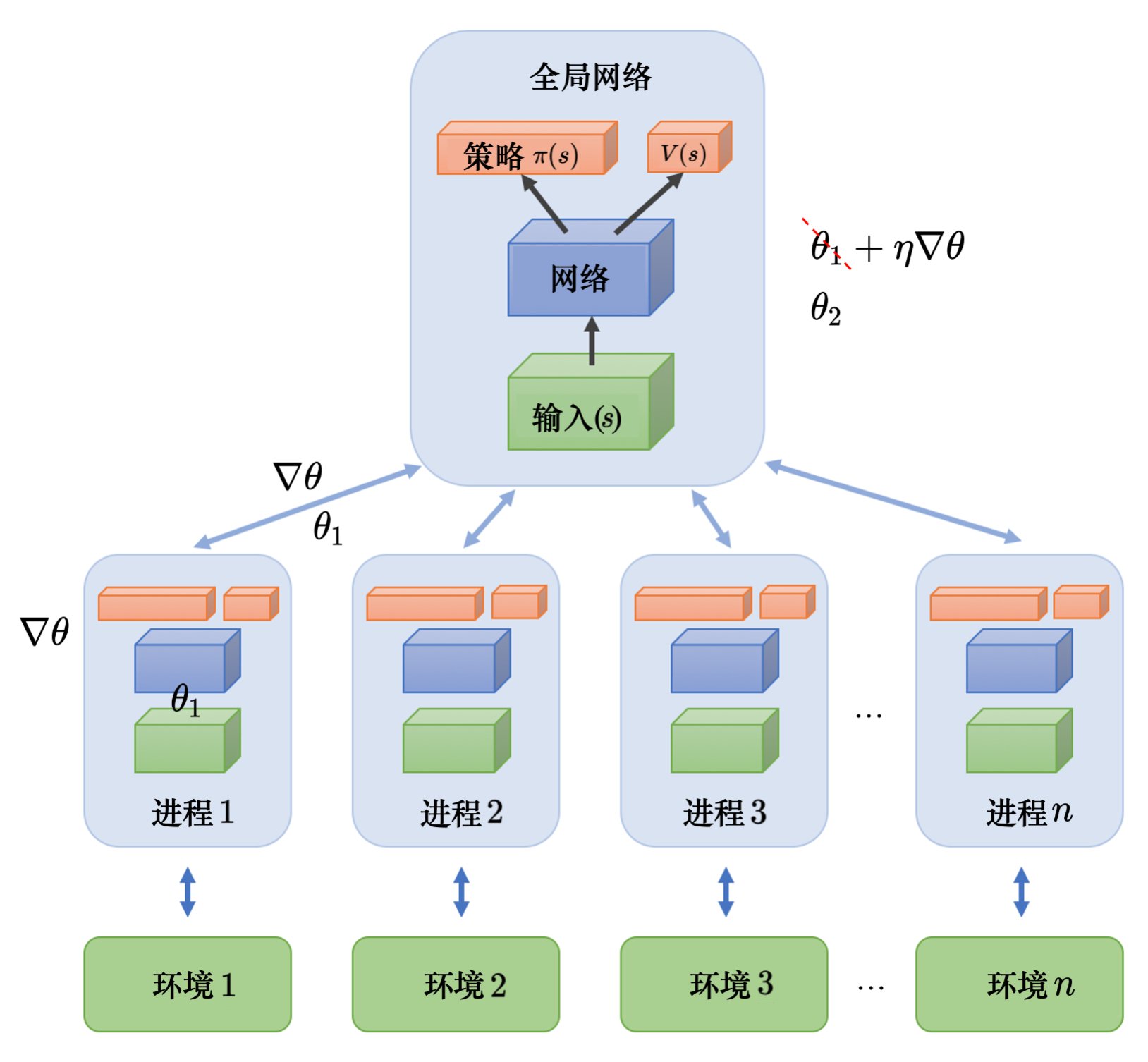
191页，第4和第5行：要用梯度去更新参数......就把梯度传 → 要用梯度去更新全局网络的参数。每个进程算出梯度以后，要把梯度传
191页，图9.6的上面一段的倒数第1行：变成 $\theta_2$了 → 变成\theta_2 了（其他进程也会更新模型）
191页，图9.6的上面一段的末尾添加文字：虽然A3C看起来属于异策略算法，但它其实是一种同策略算法。因为A3C的演员和评论员只使用当前策略采样的数据来计算梯度。因此，A3C不存储历史数据，其主要通过平行探索（parallel exploration）来保持训练的稳定性。
191页，图9.6替换成下图：

191页，图9.6加参考文献：Arthur Juliani的文章“Simple Reinforcement Learning with Tensorflow Part 8: Asynchronous Actor-Critic Agents (A3C)”
195页，9.7节的第1段的第1行：生产对抗网络 → 生成对抗网络
200页，第6行：它的目标是要让每一场表演都获得观众尽可能多的欢呼声与掌声，也就是要最大化未来的总奖励 → 评论员的最终目标是让演员的表演获得观众尽可能多的欢呼声和掌声，从而最大化未来的总收益
201页，图10.7的上面一段的倒数第1行：均方差 → 均方误差（mean squared error，MSE）
201页，图10.7的下面一段的第3行：之间的一个均方差 → 之间的均方误差
202页，图10.8的下面一段的第4行：时间相关的 OU 噪声 → 时间相关的奥恩斯坦-乌伦贝克（Ornstein-Uhlenbeck，OU）噪声
203页，式(10.1)上面一段的第2行：均方差 → 均方误差
207页，10.4.3节的标题：Ornstein-Uhlenbeck 噪声 → OU 噪声
207页，10.4.3节的第1段的第1行：奥恩斯坦-乌伦贝克（Ornstein-Uhlenbeck，OU）噪声 → OU 噪声
229页，第2行：很强的序列 → 很长的序列
242页，13.4.3节上面一段的第1行：均方差损失 → 均方误差损失

13 KiB Raw Blame History Unescape Escape

纸质版勘误修订表

第1版第3次印刷（2022.07）

第1版第2次印刷（2022.06）

第1版第1次印刷（2022.03）

13 KiB

Raw Blame History