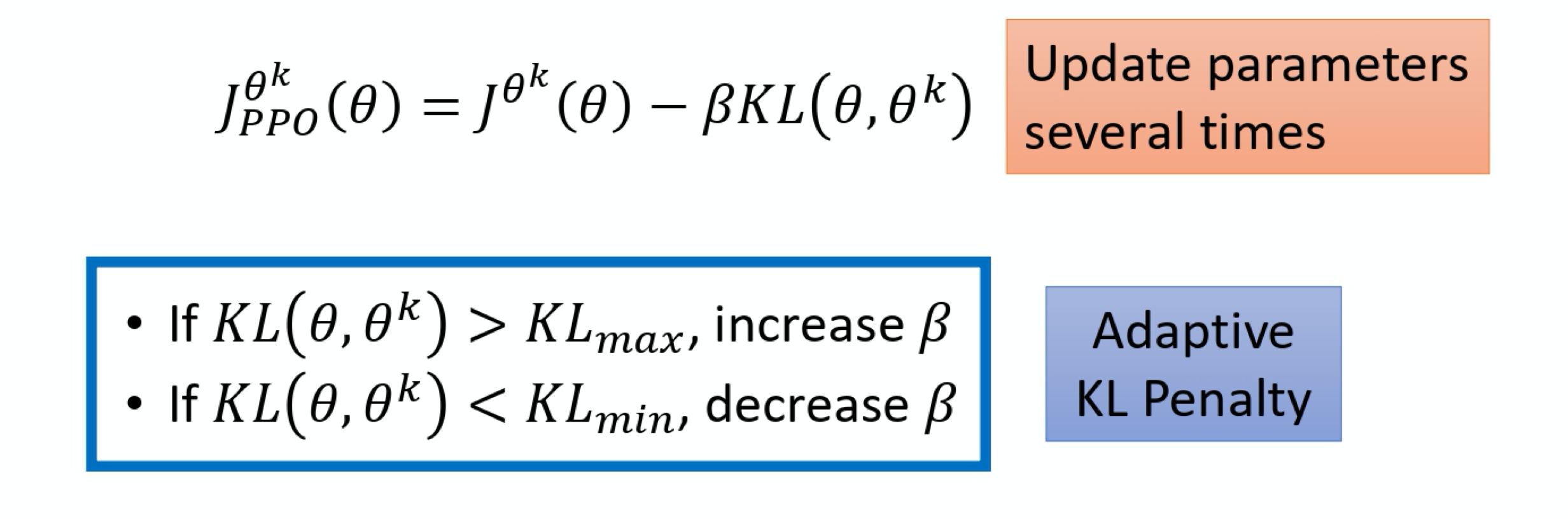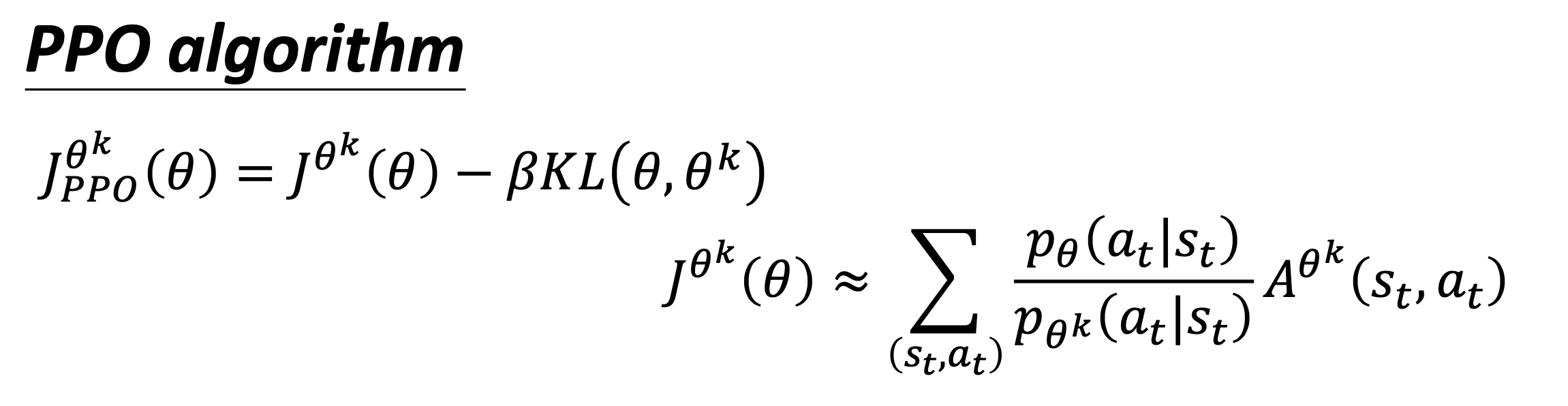easy-rl/docs/chapter2/chapter2.md

PPO

From On-policy to Off-policy

在讲 PPO 之前，我们先讲一下 on-policy 和 off-policy 这两种 training 方法的区别。 在 reinforcement learning 里面，我们要 learn 的就是一个agent。

• 如果要 learn 的 agent 跟和环境互动的 agent 是同一个的话， 这个叫做on-policy(同策略)。
• 如果要 learn 的 agent 跟和环境互动的 agent 不是同一个的话， 那这个叫做off-policy(异策略)。

比较拟人化的讲法是如果要学习的那个 agent，一边跟环境互动，一边做学习这个叫 on-policy。 如果它在旁边看别人玩，通过看别人玩来学习的话，这个叫做 off-policy。

为什么我们会想要考虑 off-policy ？让我们来想想 policy gradient。Policy gradient 是 on-policy 的做法，因为在做policy gradient 时，我们会需要有一个agent、一个policy 和 一个actor。这个actor 先去跟环境互动去搜集资料，搜集很多的$\tau$，根据它搜集到的资料，会按照 policy gradient 的式子去 update policy 的参数。所以 policy gradient 是一个 on-policy 的 algorithm。

PPO 是 policy gradient 的一个变形，它是现在 OpenAI default reinforcement learning 的 algorithm。

\nabla \bar{R}_{\theta}=E_{\tau \sim p_{\theta}(\tau)}\left[R(\tau) \nabla \log p_{\theta}(\tau)\right]

问题是上面这个 update 的式子中的 E_{\tau \sim p_{\theta}(\tau)} 应该是你现在的 policy \theta 所 sample 出来的 trajectory \tau 做 expectation。一旦 update 了参数，从 \theta 变成 \theta' ，$p_\theta(\tau)$这个概率就不对了，之前sample 出来的 data 就变的不能用了。所以 policy gradient 是一个会花很多时间来 sample data 的 algorithm，你会发现大多数时间都在 sample data，agent 去跟环境做互动以后，接下来就要 update 参数。你只能 update 参数一次。接下来你就要重新再去 collect data， 然后才能再次update 参数，这显然是非常花时间的。所以我们想要从 on-policy 变成 off-policy。 这样做就可以用另外一个policy， 另外一个actor \theta' 去跟环境做互动。用 \theta' collect 到的data 去训练 $\theta$。假设我们可以用 \theta' collect 到的data 去训练 $\theta$，意味着说我们可以把\theta' collect 到的data 用非常多次。我们可以执行 gradient ascent 好几次，我们可以 update 参数好几次， 都只要用同一笔data 就好了。因为假设 \theta 有能力学习另外一个actor \theta' 所 sample 出来的 data 的话， 那\theta' 就只要sample 一次，也许sample 多一点的data， 让\theta 去update 很多次，这样就会比较有效率。

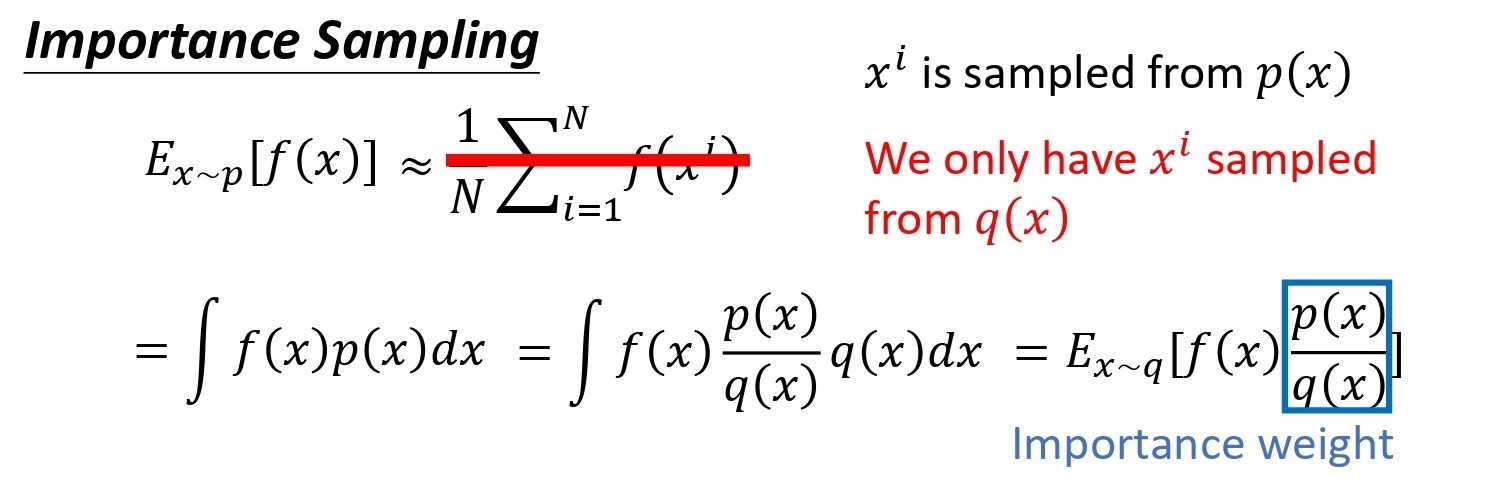
具体怎么做呢？这边就需要介绍 important sampling 的概念。假设你有一个function $f(x)$，你要计算从 p 这个 distribution sample x，再把 x 带到 f 里面，得到$f(x)$。你要该怎么计算这个 f(x) 的期望值？假设你不能对 p 这个distribution 做积分的话，那你可以从 p 这个 distribution 去 sample 一些data $x^i$。把 x^i 代到 f(x) 里面，然后取它的平均值，就可以近似 f(x) 的期望值。

现在有另外一个问题，我们没有办法从 p 这个 distribution 里面 sample data。假设我们不能从 p sample data，只能从另外一个 distribution q 去 sample data，q 可以是任何 distribution。我们不能够从 p 去sample data，但可以从 q 去 sample $x$。我们从 q 去 sample x^i 的话就不能直接套下面的式子。

E_{x \sim p}[f(x)] \approx \frac{1}{N} \sum_{i=1}^N f(x^i)

因为上式是假设你的 x 都是从 p sample 出来的。所以做一个修正，修正是这样子的。期望值$E_{x \sim p}[f(x)]$其实就是$\int f(x) p(x) dx$，我们对其做如下的变换：

\int f(x) p(x) d x=\int f(x) \frac{p(x)}{q(x)} q(x) d x=E_{x \sim q}[f(x){\frac{p(x)}{q(x)}}]

我们就可以写成对 q 里面所 sample 出来的 x 取期望值。我们从q 里面 sample x，然后再去计算$f(x) \frac{p(x)}{q(x)}$，再去取期望值。所以就算我们不能从 p 里面去 sample data，只要能够从 q 里面去sample data，然后代入上式，你就可以计算从 p 这个distribution sample x 代入 f 以后所算出来的期望值。

这边是从 q 做 sample，所以从 q 里 sample 出来的每一笔data，你需要乘上一个 weight 来修正这两个 distribution 的差异，weight 就是$\frac{p(x)}{q(x)}$。q(x) 可以是任何 distribution，唯一的限制就是 q(x) 的概率是 0 的时候，p(x) 的概率不为 0，不然这样会没有定义。假设 q(x) 的概率是 0 的时候，p(x) 的概率也都是 0 的话，那这样 p(x) 除以 $q(x)$是有定义的。所以这个时候你就可以 apply important sampling 这个技巧。你就可以从 p 做 sample 换成从 q 做 sample。

Important sampling 有一些 issue。虽然理论上你可以把 p 换成任何的 q。但是在实现上， p 和 q 不能够差太多。差太多的话，会有一些问题。什么样的问题呢？

E_{x \sim p}[f(x)]=E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]

虽然上式成立。但上式左边是f(x) 的期望值，它的distribution 是 p，上式右边是f(x) \frac{p(x)}{q(x)} 的期望值，它的distribution 是 q。如果不是算期望值，而是算 variance 的话。这两个variance 是不一样的。两个 random variable 的 mean 一样，并不代表它的 variance 一样。

我们可以代一下方差的公式

\operatorname{Var}_{x \sim p}[f(x)]=E_{x \sim p}\left[f(x)^{2}\right]-\left(E_{x \sim p}[f(x)]\right)^{2}

\begin{aligned}
\operatorname{Var}_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right] &=E_{x \sim q}\left[\left(f(x) \frac{p(x)}{q(x)}\right)^{2}\right]-\left(E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]\right)^{2} \\
&=E_{x \sim p}\left[f(x)^{2} \frac{p(x)}{q(x)}\right]-\left(E_{x \sim p}[f(x)]\right)^{2}
\end{aligned}

\operatorname{Var}_{x \sim p}[f(x)] 和 \operatorname{Var}_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right] 的差别在第一项是不同的， \operatorname{Var}_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right] 的第一项多乘了$\frac{p(x)}{q(x)}$，如果\frac{p(x)}{q(x)} 差距很大的话， $\operatorname{Var}_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]$的 variance 就会很大。所以虽然理论上它们的expectation 一样，也就是说，你只要对 p 这个distribution sample 够多次，q 这个distribution sample 够多，你得到的结果会是一样的。但是假设你sample 的次数不够多，因为它们的variance 差距是很大的，所以你就有可能得到非常大的差别。

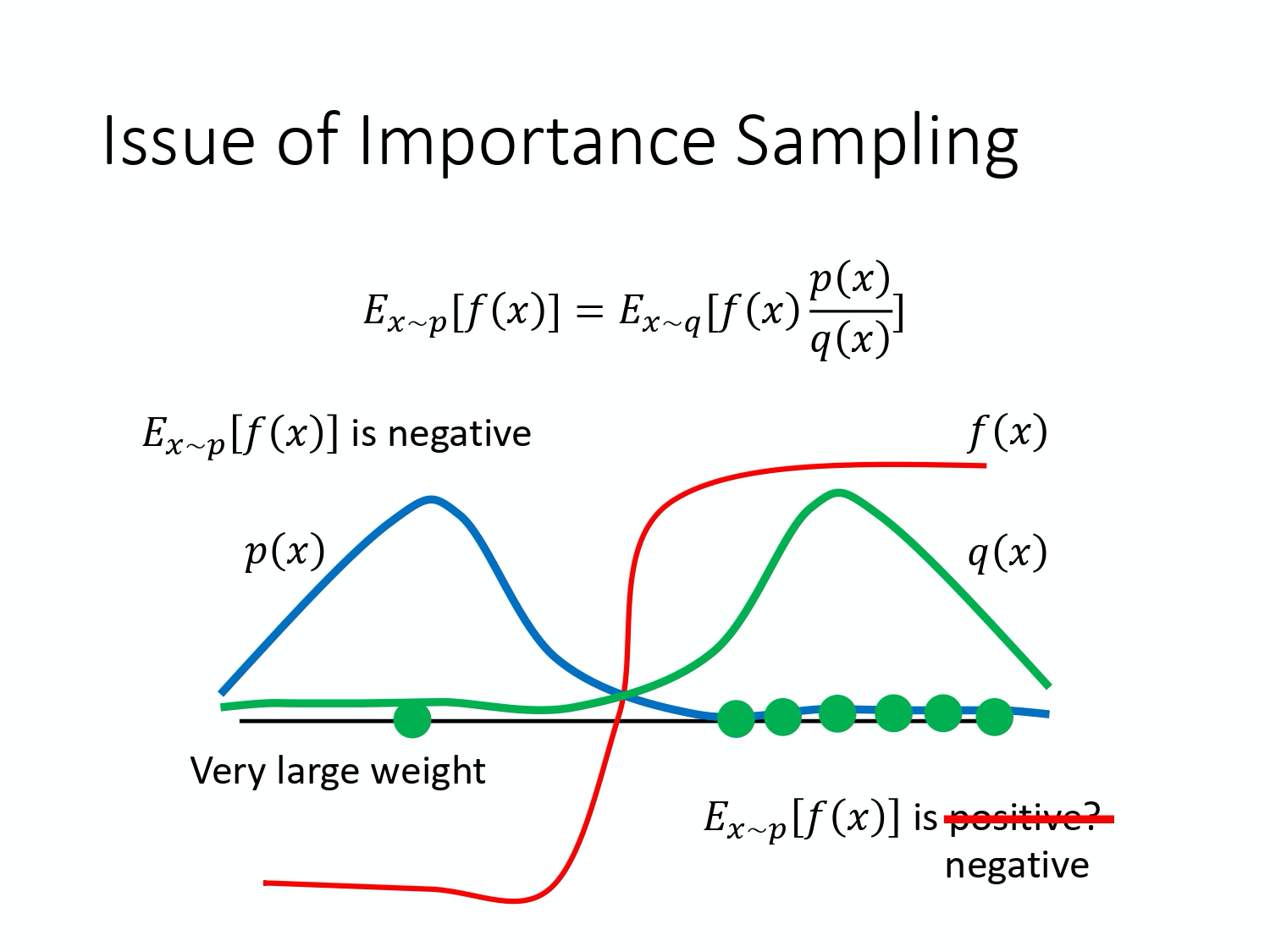
举个例子，当 p(x) 和 q(x) 差距很大的时候，会发生什么样的问题。假设蓝线是 p(x) 的distribution，绿线是 q(x) 的 distribution，红线是 $f(x)$。如果我们要计算$f(x)$的期望值，从 p(x) 这个distribution 做 sample 的话，那显然 E_{x \sim p}[f(x)] 是负的，因为左边那块区域 p(x) 的概率很高，所以要 sample 的话，都会 sample 到这个地方，而 f(x) 在这个区域是负的， 所以理论上这一项算出来会是负。

接下来我们改成从 q(x) 这边做 sample，因为 q(x) 在右边这边的概率比较高，所以如果你sample 的点不够的话，那你可能都只sample 到右侧。如果你都只 sample 到右侧的话，你会发现说，算 $E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]$这一项，搞不好还应该是正的。你这边sample 到这些点，然后你去计算它们的$f(x) \frac{p(x)}{q(x)}$都是正的，所以你sample 到这些点都是正的。 你取期望值以后，也都是正的。为什么会这样，因为你 sample 的次数不够多，因为假设你sample 次数很少，你只能sample 到右边这边。左边这边虽然概率很低，但也不是没有可能被 sample 到。假设你今天好不容易 sample 到左边的点，因为左边的点，p(x) 和 q(x) 是差很多的， 这边 p(x) 很小，q(x) 很大。今天 f(x) 好不容易终于 sample 到一个负的，这个负的就会被乘上一个非常大的 weight ，这样就可以平衡掉刚才那边一直 sample 到 positive 的 value 的情况。最终你算出这一项的期望值，终究还是负的。但前提是你要sample 够多次，这件事情才会发生。但有可能sample 不够，$E_{x \sim p}[f(x)]$跟$E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right]$就有可能有很大的差距。这就是 importance sampling 的问题。

现在要做的事情就是把 importance sampling 用在 off-policy 的 case。把 on-policy training 的algorithm 改成 off-policy training 的 algorithm。怎么改呢，之前我们是拿 \theta 这个policy 去跟环境做互动，sample 出trajectory $\tau$，然后计算$R(\tau) \nabla \log p_{\theta}(\tau)$。

现在我们不用\theta 去跟环境做互动，假设有另外一个 policy $\theta'$，它就是另外一个actor。它的工作是他要去做demonstration，\theta' 的工作是要去示范给\theta 看。它去跟环境做互动，告诉 \theta 说，它跟环境做互动会发生什么事。然后，借此来训练$\theta$。我们要训练的是\theta ，\theta' 只是负责做 demo，负责跟环境做互动。

我们现在的\tau 是从 \theta' sample 出来的，是拿 \theta' 去跟环境做互动。所以sample 出来的 \tau 是从 \theta' sample 出来的，这两个distribution 不一样。但没有关系，假设你本来是从 p 做sample，但你发现你不能够从 p 做sample，所以我们不拿\theta 去跟环境做互动。你可以把 p 换 q，然后在后面这边补上一个 importance weight。现在的状况就是一样，把 \theta 换成 \theta' 后，要补上一个importance weight $\frac{p_{\theta}(\tau)}{p_{\theta^{\prime}}(\tau)}$。这个 importance weight 就是某一个 trajectory \tau 用 \theta 算出来的概率除以这个 trajectory $\tau$，用\theta' 算出来的概率。这一项是很重要的，因为今天你要learn 的是actor \theta 和 \theta' 是不太一样的。\theta' 会见到的情形跟 \theta 见到的情形不见得是一样的，所以中间要做一个修正的项。

现在的data 不是从\theta sample 出来，是从 \theta' sample 出来的。从\theta 换成\theta' 有什么好处呢？因为现在跟环境做互动是\theta' 而不是$\theta$。所以 sample 出来的东西跟 \theta 本身是没有关系的。所以你就可以让 \theta' 做互动 sample 一大堆的data，\theta 可以update 参数很多次。然后一直到 \theta train 到一定的程度，update 很多次以后，\theta' 再重新去做sample，这就是on-policy 换成off-policy 的妙用。

实际在做 policy gradient 的时候，我们并不是给整个 trajectory \tau 都一样的分数，而是每一个state-action 的pair 会分开来计算。实际上 update gradient 的时候，我们的式子是长这样子的。

=E_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta}}\left[A^{\theta}\left(s_{t}, a_{t}\right) \nabla \log p_{\theta}\left(a_{t}^{n} | s_{t}^{n}\right)\right]

我们用 \theta 这个actor 去sample 出s_t 跟$a_t$，sample 出state 跟action 的pair，我们会计算这个state 跟action pair 它的advantage， 就是它有多好。$A^{\theta}\left(s_{t}, a_{t}\right)$就是 accumulated 的 reward 减掉 bias，这一项就是估测出来的。它要估测的是，在state s_t 采取action a_t 是好的，还是不好的。那接下来后面会乘上$\nabla \log p_{\theta}\left(a_{t}^{n} | s_{t}^{n}\right)$，也就是说如果$A^{\theta}\left(s_{t}, a_{t}\right)$是正的，就要增加概率， 如果是负的，就要减少概率。

那现在用了 importance sampling 的技术把 on-policy 变成 off-policy，就从 \theta 变成 $\theta'$。所以现在$s_t$、a_t 是\theta' ，另外一个actor 跟环境互动以后所 sample 到的data。 但是拿来训练要调整参数是 model $\theta$。因为 \theta' 跟 \theta 是不同的model，所以你要做一个修正的项。这项修正的项，就是用 importance sampling 的技术，把$s_t$、a_t 用 \theta sample 出来的概率除掉$s_t$、a_t 用 \theta' sample 出来的概率。

=E_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta^{\prime}}}\left[\frac{P_{\theta}\left(s_{t}, a_{t}\right)}{P_{\theta^{\prime}}\left(s_{t}, a_{t}\right)} A^{\theta}\left(s_{t}, a_{t}\right) \nabla \log p_{\theta}\left(a_{t}^{n} | s_{t}^{n}\right)\right]

这边 A^{\theta}(s_t,a_t) 有一个上标 $\theta$，\theta 代表说这个是 actor \theta 跟环境互动的时候所计算出来的 A。但是实际上从 \theta 换到 \theta' 的时候，A^{\theta}(s_t,a_t) 应该改成 $A^{\theta'}(s_t,a_t)$，为什么？A 这一项是想要估测说现在在某一个 state 采取某一个 action，接下来会得到 accumulated reward 的值减掉base line 。你怎么估 A 这一项，你就会看在 state $s_t$，采取 action $a_t$，接下来会得到的reward 的总和，再减掉baseline。之前是 \theta 在跟环境做互动，所以你观察到的是 \theta 可以得到的reward。但现在是 \theta' 在跟环境做互动，所以你得到的这个advantage， 其实是根据 \theta' 所estimate 出来的advantage。但我们现在先不要管那么多， 我们就假设这两项可能是差不多的。

那接下来，我们可以拆解 p_{\theta}\left(s_{t}, a_{t}\right) 和 $p_{\theta'}\left(s_{t}, a_{t}\right)$，即

\begin{aligned}
p_{\theta}\left(s_{t}, a_{t}\right)&=p_{\theta}\left(a_{t}|s_{t}\right) p_{\theta}(s_t) \\
p_{\theta'}\left(s_{t}, a_{t}\right)&=p_{\theta'}\left(a_{t}|s_{t}\right) p_{\theta'}(s_t) 
\end{aligned}

于是我们得到下式：

=E_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta^{\prime}}}\left[\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)} \frac{p_{\theta}\left(s_{t}\right)}{p_{\theta^{\prime}}\left(s_{t}\right)} A^{\theta^{\prime}}\left(s_{t}, a_{t}\right) \nabla \log p_{\theta}\left(a_{t}^{n} | s_{t}^{n}\right)\right]

然后这边需要做一件事情是，假设 model 是 \theta 的时候，你看到s_t 的概率，跟 model 是\theta' 的时候，你看到s_t 的概率是差不多的，即$p_{\theta}(s_t)=p_{\theta'}(s_t)$。因为它们是一样的，所以你可以把它删掉，即

=E_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta^{\prime}}}\left[\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)} A^{\theta^{\prime}}\left(s_{t}, a_{t}\right) \nabla \log p_{\theta}\left(a_{t}^{n} | s_{t}^{n}\right)\right]  \quad(1)

为什么可以假设它是差不多的。举例来说，会看到什么state 往往跟你会采取什么样的action 是没有太大的关系的。比如说你玩不同的 Atari 的游戏，其实你看到的游戏画面都是差不多的，所以也许不同的 \theta 对 s_t 是没有影响的。但是有一个更直觉的理由就是这一项到时候真的要你算，你会算吗？因为想想看这项要怎么算，这一项你还要说我有一个参数$\theta$，然后拿\theta 去跟环境做互动，算s_t 出现的概率，这个你根本很难算。尤其是你如果 input 是image 的话， 同样的 s_t 根本就不会出现第二次。你根本没有办法估这一项， 所以干脆就无视这个问题。

但是 $p_{\theta}(a_t|s_t)$很好算。你手上有\theta 这个参数，它就是个network。你就把s_t 带进去，s_t 就是游戏画面，你把游戏画面带进去，它就会告诉你某一个state 的 a_t 概率是多少。我们其实有个 policy 的network，把 s_t 带进去，它会告诉我们每一个 a_t 的概率是多少。所以 \frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)} 这一项，你只要知道\theta 和 \theta' 的参数就可以算。

现在我们得到一个新的objective function。

J^{\theta^{\prime}}(\theta)=E_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta^{\prime}}}\left[\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)} A^{\theta^{\prime}}\left(s_{t}, a_{t}\right)\right]

式(1)是 gradient，其实我们可以从 gradient 去反推原来的 objective function。这边有一个公式

\nabla f(x)=f(x) \nabla \log f(x)

我们可以用这个公式来反推objective function，要注意一点，对 \theta 求梯度时，p_{\theta^{\prime}}(a_{t} | s_{t}) 和 A^{\theta^{\prime}}\left(s_{t}, a_{t}\right) 都是常数。

所以实际上，当我们apply importance sampling 的时候，要去optimize 的那一个objective function 就长这样子，我们把它写作$J^{\theta^{\prime}}(\theta)$。为什么写成J^{\theta^{\prime}}(\theta) 呢，这个括号里面那个\theta 代表我们要去optimize 的那个参数。\theta' 是说我们拿 \theta' 去做demonstration，就是现在真正在跟环境互动的是$\theta'$。因为 \theta 不跟环境做互动，是 \theta' 在跟环境互动。

然后你用\theta' 去跟环境做互动，sample 出$s_t$、a_t 以后，你要去计算s_t 跟a_t 的advantage，然后你再去把它乘上$\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)}$。$\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)}$是好算的，A^{\theta^{\prime}}\left(s_{t}, a_{t}\right) 可以从这个 sample 的结果里面去估测出来的，所以 J^{\theta^{\prime}}(\theta) 是可以算的。实际上在 update 参数的时候，就是按照式(1) 来 update 参数。

PPO

我们可以把 on-policy 换成 off-policy，但 importance sampling 有一个 issue，如果 p_{\theta}\left(a_{t} | s_{t}\right) 跟 p_{\theta'}\left(a_{t} | s_{t}\right) 差太多的话，这两个 distribution 差太多的话，importance sampling 的结果就会不好。怎么避免它差太多呢？这个就是 Proximal Policy Optimization (PPO) 在做的事情。它实际上做的事情就是这样，在 off-policy 的方法里要optimize 的是 $J^{\theta^{\prime}}(\theta)$。但是这个 objective function 又牵涉到 importance sampling。在做 importance sampling 的时候，p_{\theta}\left(a_{t} | s_{t}\right) 不能跟 $p_{\theta'}\left(a_{t} | s_{t}\right)$差太多。你做 demonstration 的 model 不能够跟真正的 model 差太多，差太多的话 importance sampling 的结果就会不好。我们在 training 的时候，多加一个 constrain。这个constrain 是 \theta 跟 \theta' output 的 action 的 KL divergence，简单来说，这一项的意思就是要衡量说 \theta 跟 \theta' 有多像。

然后我们希望在 training 的过程中，learn 出来的 \theta 跟 \theta' 越像越好。因为如果 \theta 跟 \theta' 不像的话，最后的结果就会不好。所以在 PPO 里面有两个式子，一方面是 optimize 本来要 optimize 的东西，但再加一个 constrain。这个 constrain 就好像那个 regularization 的 term 一样，在做 machine learning 的时候不是有 L1/L2 的regularization。这一项也很像 regularization，这样 regularization 做的事情就是希望最后 learn 出来的 \theta 不要跟 \theta' 太不一样。

PPO 有一个前身叫做TRPO，TRPO 的式子如下式所示。

\begin{aligned}
J_{T R P O}^{\theta^{\prime}}(\theta)=E_{\left(s_{t}, a_{t}\right) \sim \pi_{\theta^{\prime}}}\left[\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)} A^{\theta^{\prime}}\left(s_{t}, a_{t}\right)\right] \\ \\
\mathrm{KL}\left(\theta, \theta^{\prime}\right)<\delta
\end{aligned}

它与PPO不一样的地方 是 constrain 摆的位置不一样，PPO是直接把 constrain 放到你要 optimize 的那个式子里面，然后你就可以用 gradient ascent 的方法去 maximize 这个式子。但 TRPO 是把 KL divergence 当作constrain，它希望 \theta 跟 \theta' 的 KL divergence 小于一个$\delta$。如果你是用 gradient based optimization 时，有 constrain 是很难处理的。

PPO是很难处理的，因为它是把 KL divergence constrain 当做一个额外的 constrain，没有放 objective 里面，所以它很难算。所以不想搬石头砸自己的脚的话， 你就用PPO 不要用TRPO。看文献上的结果是，PPO 跟TRPO 可能 performance 差不多，但 PPO 在实现上比 TRPO 容易的多。

KL divergence 到底指的是什么？这边我是直接把 KL divergence 当做一个 function，input 是 \theta 跟 $\theta'$，但我的意思并不是说把 \theta 或 \theta' 当做一个distribution，算这两个distribution 之间的距离，我不是这个意思。所谓的 \theta 跟 \theta' 的距离并不是参数上的距离，而是 behavior 上的距离。

假设你有一个model，有一个actor 它是$\theta$，你有另外一个actor 的参数是\theta' ，所谓参数上的距离就是你算这两组参数有多像。我今天所讲的不是参数上的距离， 而是它们行为上的距离。就是你先带进去一个state s，它会对这个 action 的 space output 一个 distribution。假设你有 3 个actions，3 个可能的 actions 就 output 3 个值。那今天所指的 distance 是behavior distance。也就是说，给同样的 state 的时候，输出 action 之间的差距。这两个 actions 的 distribution 都是一个概率分布。所以就可以计算这两个概率分布的 KL divergence。把不同的 state output 的这两个 distribution 的KL divergence 平均起来才是我这边所指的两个 actor 间的 KL divergence。你可能说怎么不直接算这个 \theta 或 \theta' 之间的距离，甚至不要用KL divergence 算，L1 跟 L2 的 norm 也可以保证 \theta 跟 \theta' 很接近啊。在做reinforcement learning 的时候，之所以我们考虑的不是参数上的距离，而是 action 上的距离，是因为很有可能对 actor 来说，参数的变化跟 action 的变化不一定是完全一致的。有时候你参数小小变了一下，它可能 output 的行为就差很多。或是参数变很多，但 output 的行为可能没什么改变。**所以我们真正在意的是这个actor 它的行为上的差距，而不是它们参数上的差距。**所以在做PPO 的时候，所谓的 KL divergence 并不是参数的距离，而是action 的距离。

我们来看一下PPO1 的algorithm。它先initial 一个policy 的参数$\theta^0$。然后在每一个iteration 里面呢，你要用参数$\theta^k$，\theta^k 就是你在前一个training 的iteration得到的actor 的参数，你用\theta^k 去跟环境做互动，sample 到一大堆 state-action 的pair。

然后你根据\theta^k 互动的结果，估测一下$A^{\theta^{k}}\left(s_{t}, a_{t}\right)$。然后你就 apply PPO 的 optimization 的 formulation。但跟原来的policy gradient 不一样，原来的 policy gradient 只能 update 一次参数，update 完以后，你就要重新 sample data。但是现在不用，你拿 \theta^k 去跟环境做互动，sample 到这组 data 以后，你可以让 \theta update 很多次，想办法去 maximize objective function。这边 \theta update 很多次没有关系，因为我们已经有做 importance sampling，所以这些experience，这些 state-action 的 pair 是从 \theta^k sample 出来的没有关系。\theta 可以 update 很多次，它跟 \theta^k 变得不太一样也没有关系，你还是可以照样训练 $\theta$。

在PPO 的paper 里面还有一个 adaptive KL divergence，这边会遇到一个问题就是 \beta 要设多少，它就跟那个regularization 一样。regularization 前面也要乘一个weight，所以这个 KL divergence 前面也要乘一个 weight，但 \beta 要设多少呢？所以有个动态调整 \beta 的方法。在这个方法里面呢，你先设一个 KL divergence，你可以接受的最大值。然后假设你发现说你 optimize 完这个式子以后，KL divergence 的项太大，那就代表说后面这个 penalize 的 term 没有发挥作用，那就把 \beta 调大。那另外你定一个 KL divergence 的最小值。如果发现 optimize 完上面这个式子以后，KL divergence 比最小值还要小，那代表后面这一项的效果太强了，你怕他只弄后面这一项，那\theta 跟\theta^k 都一样，这不是你要的，所以你这个时候你叫要减少 $\beta$。所以 \beta 是可以动态调整的。这个叫做 adaptive KL penalty。

如果你觉得算 KL divergence 很复杂。有一个PPO2。PPO2 要去 maximize 的 objective function 如下式所示，它的式子里面就没有 KL divergence 。

\begin{aligned}
J_{P P O 2}^{\theta^{k}}(\theta) \approx \sum_{\left(s_{t}, a_{t}\right)} \min &\left(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)} A^{\theta^{k}}\left(s_{t}, a_{t}\right),\right.\\
&\left.\operatorname{clip}\left(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}, 1-\varepsilon, 1+\varepsilon\right) A^{\theta^{k}}\left(s_{t}, a_{t}\right)\right)
\end{aligned}

这个式子看起来有点复杂，但实际 implement 就很简单。我们来实际看一下说这个式子到底是什么意思。 min 这个 operator 做的事情是第一项跟第二项里面选比较小的那个。第二项前面有个clip function，clip 这个function 的意思是说，在括号里面有3 项，如果第一项小于第二项的话，那就output 1-\varepsilon 。第一项如果大于第三项的话，那就output $1+\varepsilon$。 \varepsilon 是一个 hyper parameter，你要tune 的，你可以设成 0.1 或 设 0.2 。 假设这边设0.2 的话，如下式所示

\operatorname{clip}\left(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}, 0.8, 1.2\right)

如果$\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}$算出来小于0.8，那就当作0.8。如果算出来大于1.2，那就当作1.2。

我们先看一下下面这项这个算出来到底是什么的东西。

\operatorname{clip}\left(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}, 1-\varepsilon, 1+\varepsilon\right)

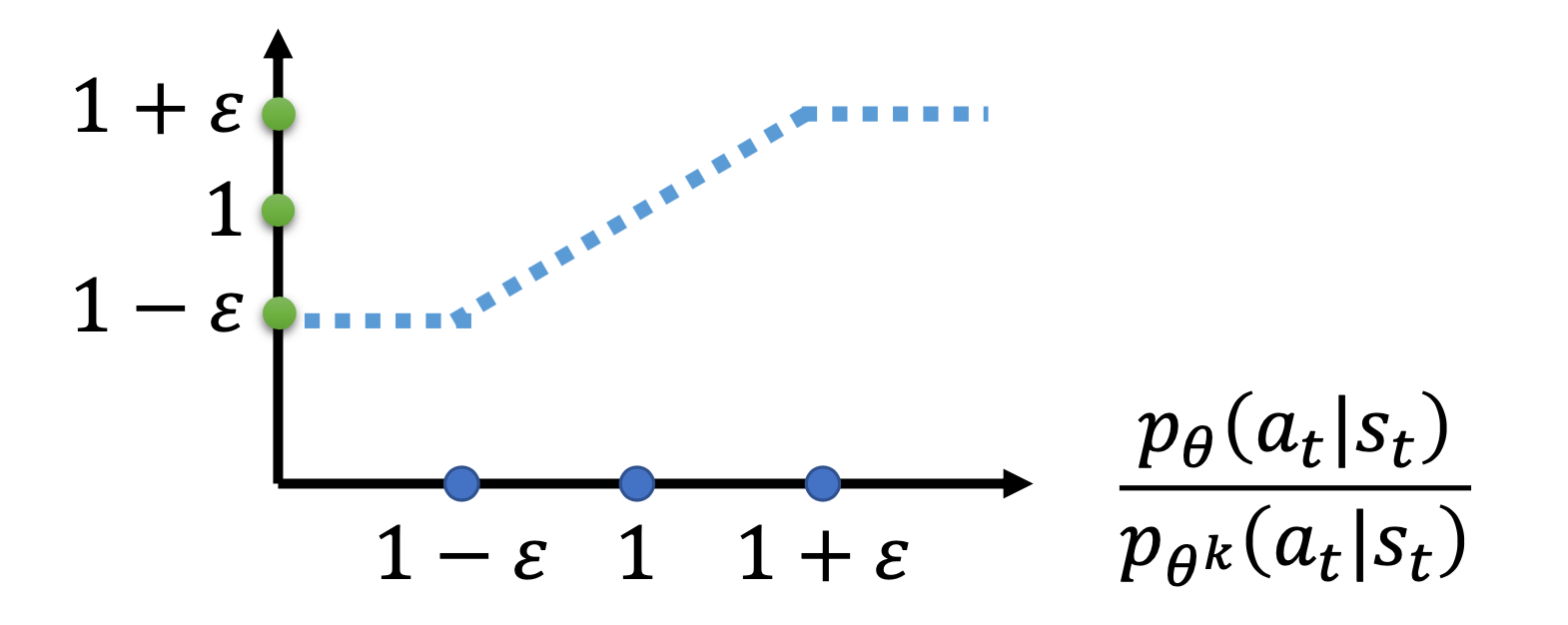
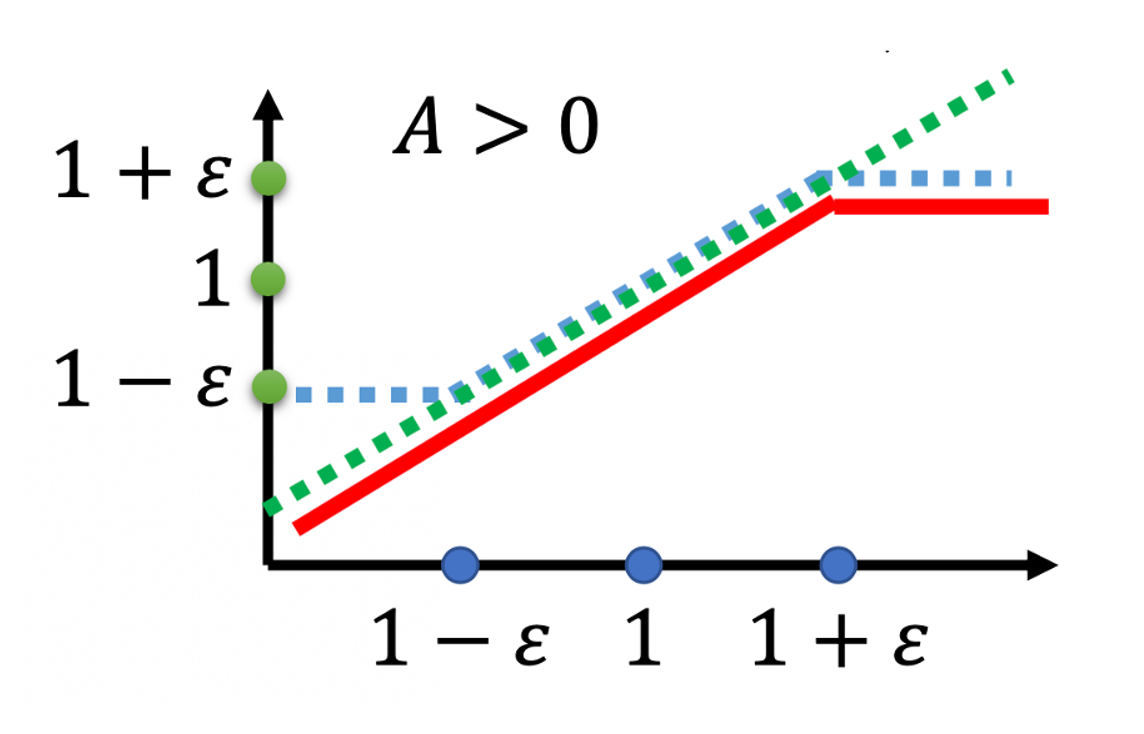
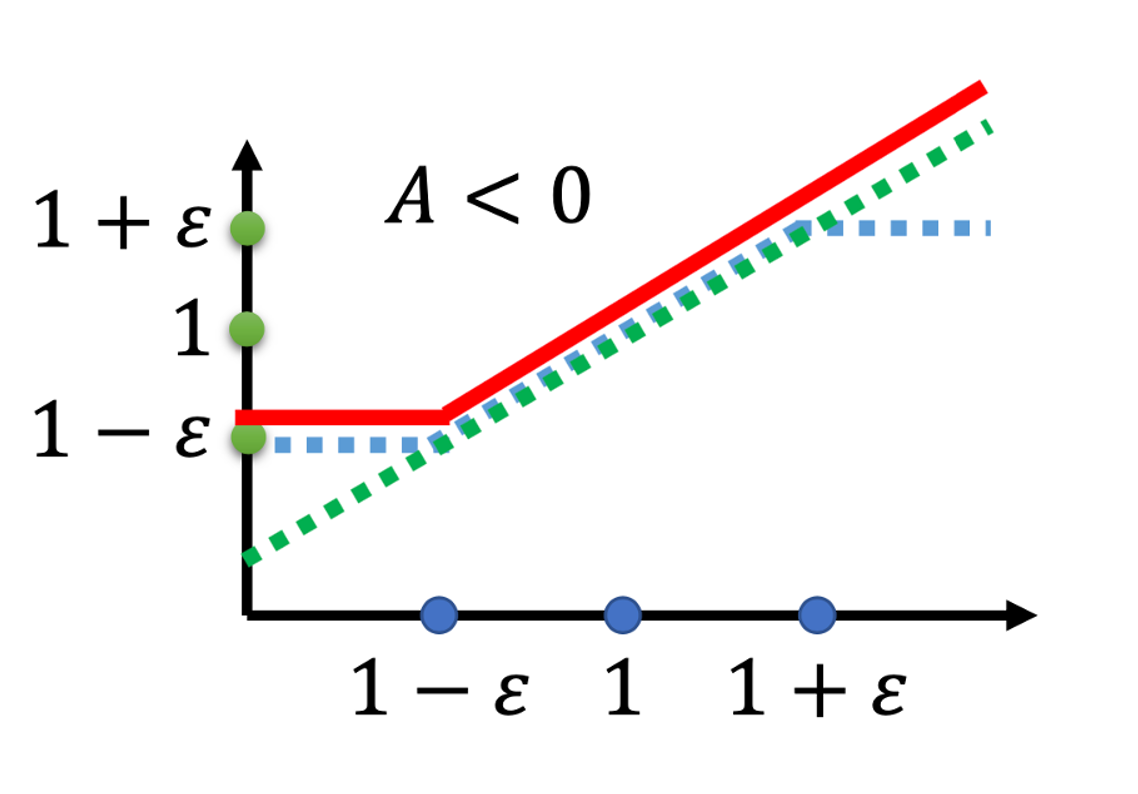
上图的横轴是 $\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}$，纵轴是 clip function 实际的输出。

• 如果 \frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)} 大于$1+\varepsilon$，输出就是$1+\varepsilon$。
• 如果小于 $1-\varepsilon$， 它输出就是 $1-\varepsilon$。
• 如果介于 1+\varepsilon 跟 1-\varepsilon 之间， 就是输入等于输出。

\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)} 是绿色的线，\operatorname{clip}\left(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}, 1-\varepsilon, 1+\varepsilon\right) 是蓝色的线。在绿色的线跟蓝色的线中间，我们要取一个最小的。假设前面乘上的这个 term A，它是大于0 的话，取最小的结果，就是红色的这一条线。

如果 A 小于0 的话，取最小的以后，就得到红色的这一条线。 这一个式子虽然看起来有点复杂，implement 起来是蛮简单的，因为这个式子想要做的事情就是希望 p_{\theta}(a_{t} | s_{t}) 跟$p_{\theta^k}(a_{t} | s_{t})$，也就是你拿来做 demonstration 的那个model， 跟你实际上 learn 的 model，在optimize 以后不要差距太大。那你要怎么让它做到不要差距太大呢？

如果 A 大于 0，也就是某一个 state-action 的pair 是好的。那我们希望增加这个state-action pair 的概率。也就是说，我们想要让 p_{\theta}(a_{t} | s_{t}) 越大越好，但它跟 p_{\theta^k}(a_{t} | s_{t}) 的比值不可以超过 $1+\varepsilon$。如果超过1+\varepsilon 的话，就没有benefit 了。红色的线就是我们的objective function，我们希望objective 越大越好，我们希望 p_{\theta}(a_{t} | s_{t}) 越大越好。但是$\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}$只要大过 $1+\varepsilon$，就没有benefit 了。

所以今天在train 的时候，当p_{\theta}(a_{t} | s_{t}) 被 train 到$\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}$大于 1+\varepsilon 时，它就会停止。

假设 p_{\theta}(a_{t} | s_{t}) 比 p_{\theta^k}(a_{t} | s_{t}) 还要小，那我们的目标是要让 p_{\theta}(a_{t} | s_{t}) 越大越好。

• 假设这个 advantage 是正的，我们希望p_{\theta}(a_{t} | s_{t}) 越大越好。假设这个 action 是好的，我们当然希望这个 action 被采取的概率越大越好。所以假设 p_{\theta}(a_{t} | s_{t}) 还比 p_{\theta^k}(a_{t} | s_{t}) 小，那就尽量把它挪大，但只要大到1+\varepsilon 就好。
• 负的时候也是一样，如果某一个state-action pair 是不好的，我们希望把 p_{\theta}(a_{t} | s_{t}) 减小。如果 p_{\theta}(a_{t} | s_{t}) 比p_{\theta^k}(a_{t} | s_{t}) 还大，那你就尽量把它压小，压到$\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{k}}\left(a_{t} | s_{t}\right)}$是1-\epsilon 的时候就停了，就不要再压得更小。

这样的好处就是， 你不会让 p_{\theta}(a_{t} | s_{t}) 跟 p_{\theta^k}(a_{t} | s_{t}) 差距太大。要 implement 这个东西，很简单。

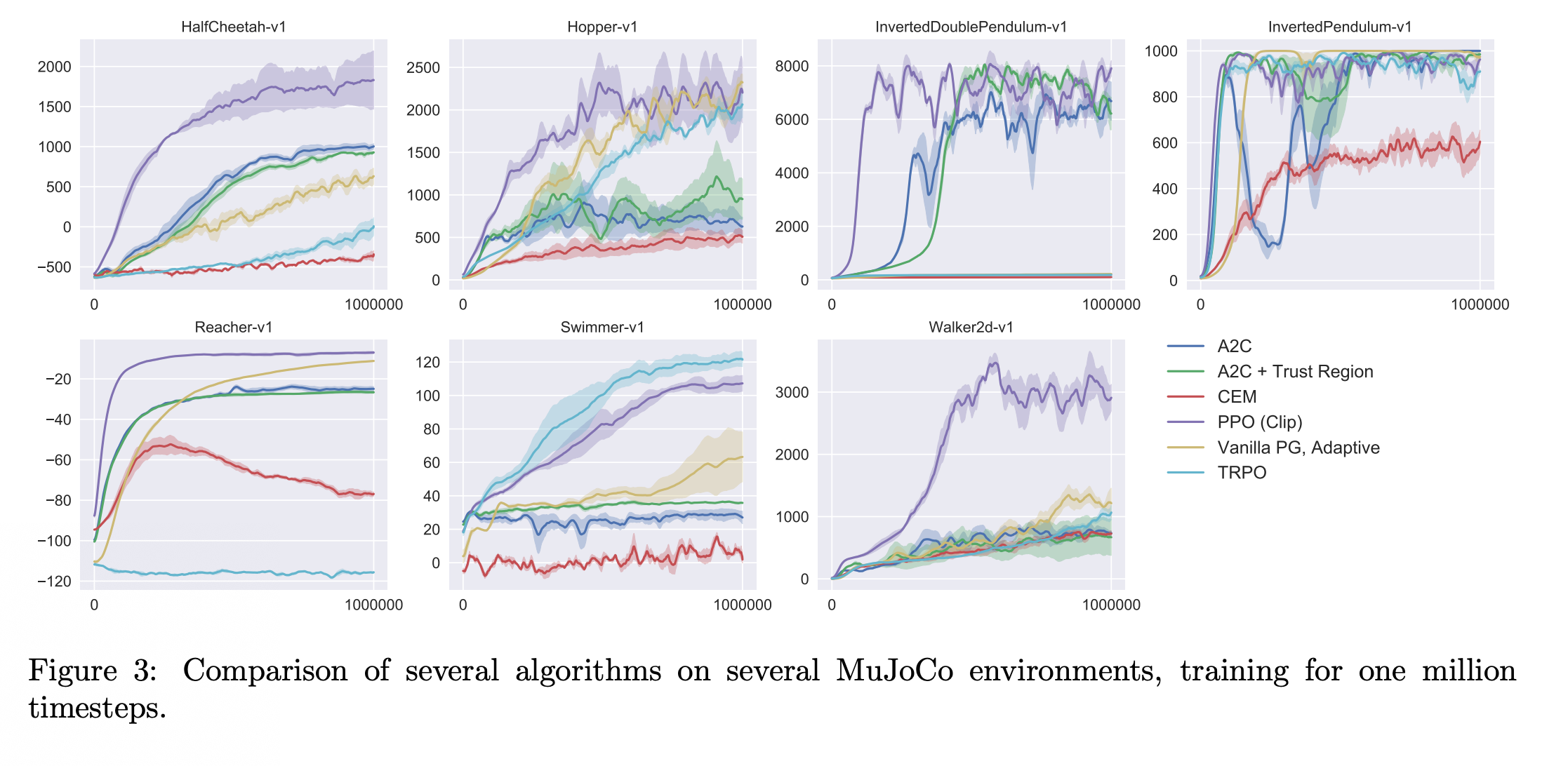上图是 PPO 跟其它方法的比较。Actor-Critic 和 A2C+Trust Region 方法是actor-critic based 的方法。PPO 是紫色线的方法，这边每张图就是某一个RL 的任务，你会发现说在多数的cases 里面，PPO 都是不错的，不是最好的，就是第二好的。